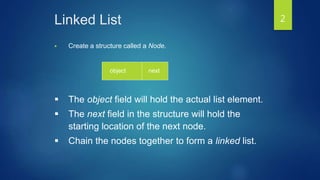
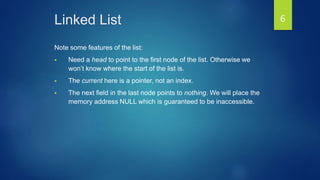
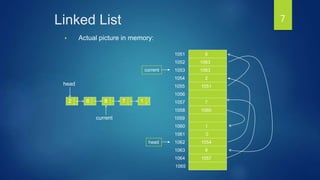
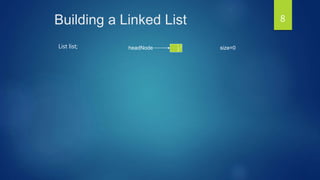
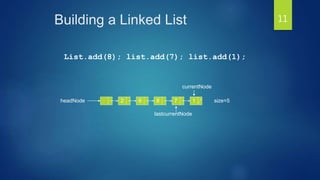
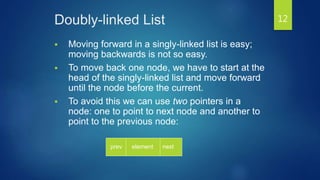
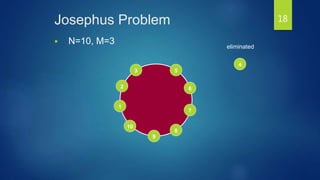
The document discusses linked lists and their features. It describes how to create a linked list node structure with an object field to hold the list element and a next field to link to the next node. It shows how to chain nodes together to form a linked list and notes that the last node points to NULL. It also introduces doubly linked lists, circular linked lists, and provides an example of how a circular linked list could solve the Josephus problem of eliminating people in a circle.

1. Lecture No.02
Data Structures

2. Linked List
 Create a structure called a Node.
object next
 The object field will hold the actual list element.
 The next field in the structure will hold the
starting location of the next node.
 Chain the nodes together to form a linked list.
2

3. Linked List
 Picture of our list (2, 6, 7, 8, 1) stored as a linked list:
2 6 8 7 1
head
current
size=5
3

4. Linked List
Note some features of the list:
 Need a head to point to the first node of the list. Otherwise we
won’t know where the start of the list is.
4

5. Linked List
Note some features of the list:
 Need a head to point to the first node of the list. Otherwise we
won’t know where the start of the list is.
 The current here is a pointer, not an index.
5

6. Linked List
Note some features of the list:
 Need a head to point to the first node of the list. Otherwise we
won’t know where the start of the list is.
 The current here is a pointer, not an index.
 The next field in the last node points to nothing. We will place the
memory address NULL which is guaranteed to be inaccessible.
6

7. Linked List
 Actual picture in memory:
1051
1052
1055
1059
1060
1061
1062
1063
1064
1056
1057
1058
1053
1054 2
6
8
7
1
1051
1063
1057
1060
0
head 1054
1063current
2 6 8 7 1
head
current
1065
7

8. Building a Linked List
headNode size=0List list;
8

9. Building a Linked List
headNode
2headNode
currentNode
size=1
lastcurrentNode
size=0List list;
list.add(2);
9

10. Building a Linked List
headNode
2headNode
currentNode
size=1
lastcurrentNode
2 6headNode
currentNode
size=2
lastcurrentNode
size=0List list;
list.add(2);
list.add(6);
10

11. Building a Linked List
List.add(8); list.add(7); list.add(1);
2 6 7 1headNode
currentNode
size=5
lastcurrentNode
8
11

12. Doubly-linked List
 Moving forward in a singly-linked list is easy;
moving backwards is not so easy.
 To move back one node, we have to start at the
head of the singly-linked list and move forward
until the node before the current.
 To avoid this we can use two pointers in a
node: one to point to next node and another to
point to the previous node:
element nextprev
12

13. Doubly-linked List
 Need to be more careful when adding or
removing a node.
 Consider add: the order in which pointers are
reorganized is important:
size=52 6 8 7 1head
current
13

14. Circularly-linked lists
 The next field in the last node in a singly-linked
list is set to NULL.
 Moving along a singly-linked list has to be done
in a watchful manner.
 Doubly-linked lists have two NULL pointers:
prev in the first node and next in the last node.
 A way around this potential hazard is to link the
last node with the first node in the list to create
a circularly-linked list.
14

15. Cicularly Linked List
 Two views of a circularly linked list:
2 6 8 7 1head
current
size=5
2
8
7
1
head
current
size=5
6
15

16. Josephus Problem
 A case where circularly linked list comes in
handy is the solution of the Josephus Problem.
 Consider there are 10 persons. They would like
to choose a leader.
 The way they decide is that all 10 sit in a circle.
 They start a count with person 1 and go in
clockwise direction and skip 3. Person 4
reached is eliminated.
 The count starts with the fifth and the next
person to go is the fourth in count.
 Eventually, a single person remains.
16

17. Josephus Problem
 N=10, M=3
9
8
7
6
5
4
3
2
1
10
17

18. Josephus Problem
 N=10, M=3
9
8
7
6
5
4
3
2
1
10
eliminated
18

19. Josephus Problem
 N=10, M=3
9
8
7
6
5
4
3
2
1
10
eliminated
19

20. Josephus Problem
 N=10, M=3
9
8
7
6
5
4
3
2
1
10
eliminated
20

21. Josephus Problem
 N=10, M=3
9
8
7
6
5
4
3
2
1
10
eliminated
21

22. Josephus Problem
 N=10, M=3
9
8
7
6
5
4
3
2
1
10
eliminated
22

23. Josephus Problem
 N=10, M=3
9
8
7
6
5
4
3
2
1
10
eliminated
23

24. Josephus Problem
 N=10, M=3
9
8
7
6
5
4
3
2
1
10
eliminated
24

25. Josephus Problem
 N=10, M=3
9
8
7
6
5
4
3
2
1
10
eliminated
25

26. Josephus Problem
 N=10, M=3
9
8
7
6
5
4
3
2
1
10
eliminated
26