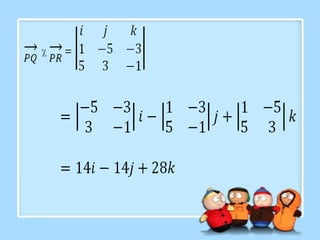Dokumen tersebut membahas tentang persamaan bidang, vektor normal, bidang sejajar, dan bidang tegak lurus. Persamaan bidang umumnya ditulis sebagai ax + by + cz + d = 0, dimana vektor normalnya adalah (a, b, c). Dua bidang dikatakan sejajar jika memiliki vektor normal yang sama atau berkelipatan, sedangkan bidang dikatakan tegak lurus jika hasil vektor normal kedua bidang bernilai n

1. BIDANG
Persamaan Bidang
Bidang Normal
Bidang Sejajar
Bidang Tegak Lurus

2. Persamaan Bidang
Diberikan titik P0 ( x0, y0,z0 ), P (x, y, z ) dan vektor tak
nol n = ( a, b, c ) sedemikian hingga
tegak lurus terhadap n
Sehingga dapat ditulis
n  = 0
n
P P0

3. Persamaan Bidang
P0 = r0 dan P = r, maka = ( r - r0 ) maka
persamaan diatas menjadi :
n  ( r - r0 ) = 0
n
P P0
( r - r0 )
Persamaan ini disebut dengan
vektor persamaan bidang dan
n disebut vektor normal

4. Persamaan Bidang
r0 = ( x0, y0,z0 ) dan r = ( x, y, z ) dan n ( a, b, c ) maka
( r - r0 ) = ( x -x0, y - y0, z - z0 ) sehingga persamaan
diatas menjadi :
a(x -x0 ) + b(y - y0 )+ c (z - z0 ) = 0
n
P P0
Persamaan ini merupakan ( r - r0 )
bentuk umum persamaan
bidang

5. Contoh Soal
Tentukan persamaan bidang yang melalui titik (3, -1,
4) dan memiliki normal vektor (2, 5, -3)!
2(x – 3) + 5(y + 1) – 3(z – 4) = 0
Bentuk sederhananya: 2x + 5y - 3z + 11 = 0

6. Dari bentuk umum persamaan bidang dan bentuk
sederhana yang didapatkan dari contoh diatas,
didapatkan persamaan baru:
ax + by + cz + d = 0
Dengan d = - (ax0 + by0 + cz0 )

7. Vektor Normal
Vektor normal tidak selalu diberikan secara jelas tetapi dapat
ditemukan dari informasi yang diberikan. Caranya dengan
menggunakan cross product
Contoh :
Carilah persamaan bidang yang
terdiri dari titik P (1, 0, -3),
Q (2, -5, -6) dan R (6, 3, -4)
R
Q
P

8. Pembahasan
Vektor dan terletak pada bidang, sehingga vektor
normalnya dapat dicari dengan cross product
= (1, -5, -3)
= (5, 3, -1)
R
Q
P

10. karena setiap vektor tak nol yang tegak lurus terhadap
bidang adalah vektor normal, maka kita bisa
menentukan vektor n agar lebih mudah
pengerjaannya:
n =
Dengan menggunakan titik P, didapatkan persamaan
bidang sebagai berikut :
( x - 1 ) - ( y – 0 ) + 2 ( z + 3 ) = 0
x – y + 2z + 5 = 0

11. Bidang Sejajar
Dua buah bidang dikatakan sejajar ( // ) jika n 1 = n2
atau berkelipatan, sehingga:
(a1, b1, c1 ) = λ (a2, b2, c2 ) dengan λ ≠ 0

12. Contoh Soal
Tentukan persamaan bidang V2 yang sejajar dengan
bidang V1 = x + y + 5z = 9 dan bidang V2 melalui titik
(0,2,1) !

13. Pembahasan
V1 = x + y + 5z = 9, karena V1 sejajar V2 maka :
n1 = n2
n1 = (1, 1, 5) maka V2 = x + y + 5z + d = 0
Karena V2 melalui titik ( 0, 2, 1 ), maka :
V2 = x + y + 5z + d = 0  0 + 2 + 5(1) + d = 0
7 + d = 0  d = -7
Sehingga persamaan bidang
V2 = x + y + 5z – 7 = 0

14. Bidang Tegak Lurus
Dua buah bidang dikatakan tegak lurus (  ) ketika
n 1.n2 = 0 sehingga (a1 a2 + b1 b2 + c1 c2 ) = 0
Contoh :
Tentukanlah apakah bidang – bidang x – y – 3z = 5
dan 2x – y + z = 1 tegak lurus.

15. Pembahasan
Jawab :
V1 = x – y – 3z = 5, maka n1 = ( 1, -1, -3 )
V2 = 2x – y + z = 1, maka n2 = ( 2, -1, 1 ).
Kedua normal bidang merupakan vector – vector
orthogonal, n1.n2 = 0
Maka : (1) (2) + (-1)(-1) + (-3) (1) = 0.
Jadi bidang V1 dan bidang V2 saling tegak lurus.

16. Latihan Soal
1. Tentukan vektor normal dan persamaan bidang yang
melalui garis r= (2 – t , 3 + 4t , - 1 - 2t ) dan titik (5, -2,
7)!
2. Tentukan persamaan bidang V2 yang tegak lurus pada
bidang V1 = x + y + z = 1 serta melalui titik (0,0,0) dan
(1,1,0) !
3. Cari persamaan bidang melalui ( -2, 1, 5 ) yang tegak
lurus bidang 4x – 2y + 2z +1 = 0 dan 3x + 3y – 6z = 5
4. Tentukanlah apakah bidang – bidang x + 2y – 2z = 5
dan 6x -3y + 2z = 8 sejajar.