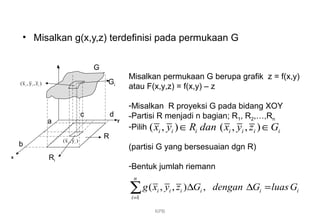
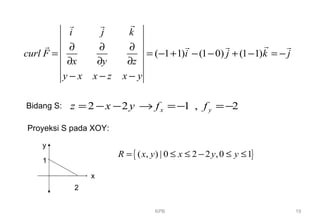
Dokumen ini membahas integral permukaan, fluks medan vektor, dan teorema divergensi Gauss serta Stokes. Penjelasan termasuk contoh penerapan dan metode perhitungan fluks melalui beberapa permukaan matematis. Topik-topik ini merupakan konsep penting dalam kalkulus multivariabel dan geometri analitik.

1. 5. INTEGRAL PERMUKAAN
KPB 1

2. • Misalkan g(x,y,z) terdefinisi pada permukaan G
x
y
z
G
b
a
c d
)y,x( ii
)z,y,x( iii
Gi
R
Ri
Misalkan permukaan G berupa grafik z = f(x,y)
atau F(x,y,z) = f(x,y) – z
-Misalkan R proyeksi G pada bidang XOY
-Partisi R menjadi n bagian; R1, R2,…,Rn
-Pilih
(partisi G yang bersesuaian dgn R)
-Bentuk jumlah riemann
( , ) ( , , )i i i i i i ix y R dan x y z G∈ ∈
1
( , , ) ,
n
i i i i i i
i
g x y z G dengan G luasG
=
∆ ∆ =∑
KPB

3. KPB 3
2 2
( , , ) ( , , ( , )) 1x y
G R
g x y z dS g x y f x y f f dA= + +∫∫ ∫∫
0
1
( , , ) lim ( , , )
n
i i i i
P
iG
g x y z dS g x y z G
→
=
= ∆∑∫∫
2 2
sec , sec 1i x yG xi yi f fγ γ∆ = ∆ ∆ = + +
γ = Sudut antara normal satuan keatas di (x,y,f(x,y)) dengan
sumbu z positif.
Maka integral permukaan dari G: R adalah proyeksi G pada XOY.

4. 2 2
( , , ) ( ( , ), , ) 1 y z
G R
g x y z dS g f y z y z f f dA= + +∫∫ ∫∫
2 2
( , , ) ( , ( , ), ) 1x z
G R
g x y z dS g x f x z z f f dA= + +∫∫ ∫∫
KPB
Dengan cara yang sama diperoleh:
1. Jika permukaan G berupa grafik ( , ) ; ( , )x f y z y z R= ∈
( proyeksi G pada YOZ), maka
2. Jika permukaan G berupa grafik ( , ) ; ( , )y f x z x z R= ∈
( proyeksi G pada XOZ), maka

5. ContohContoh
1. Hitung
G
z dS∫∫ , G adalah permukaan
2 2
4z x y= − −
Jawab.
2 2
4z x y= − −
2 2 2
4z x y= − −⇒ 2 2 2
4z x y→ + + =
G bagian atas kulit bola dengan jari-jari 2.
R (proyeksi G pada XOY) berupa lingkaran x2
+y2
=4.
2 2
4z x y= − −
( )
1/22 2
2 2
1
4 . 2
2 4
x
x
f x y x
x y
− −
= − − − =
− −
( )
1/ 22 2
2 2
1
4 . 2
2 4
y
y
f x y y
x y
− −
= − − − =
− −
Kita punya , maka
KPB

6. 2 2
1x y
G R
z dS z f f dA= + +∫∫ ∫∫
Jadi
2 2
2 2
4
4
4R
x y dA
x y
= − −
− −∫∫
2
R
dA= ∫∫
dimana daerah R={(r,θ)|0 ≤ r ≤ 2, 0≤ θ ≤ 2π }, sehingga
2
G R
z dS dA=∫∫ ∫∫
2 2 2
2
0 0 0
2 2
2 4
0 0
r dr d r d
π π
π
θ θ θ= = =∫ ∫ ∫
8 .π=
KPB
2 2 2 2
2 2
2 2 2 2 2 2 2 2
4 4
1
4 4 4 4
x x
x y x y
f f
x y x y x y x y
− −
+ + = + + =
− − − − − − − −

7. LatihanLatihan
1. Hitung , dengan G bagian kerucut z2
= x2
+ y2
di antara z = 1 dan z = 2
2 2
G
x z dS∫∫
2. Hitung
a. g(x,y,z) = x2
+ y2
+ z , dengan G: z = x+y+1, 0≤x≤1, 0≤y≤1
( , , )
G
g x y z dS∫∫
c. g(x,y,z) = x+y , dengan G: , 0≤x≤√3, 0≤y≤1
2
4 xz −=
d. g(x,y,z) = , dengan G: z =x2
-y2
, 0≤x2
+y2
≤12 2
4 4 1x y+ +
e. g(x,y,z) = x + y , dengan G adalah permukaan kubus,
0≤x≤1, 0≤y≤1, 0≤z≤1
KPB
b. g(x,y,z) = x y+z, dengan G: bagian bidang 2x-y+z = 3, di atas segitiga
dengan titik sudut (0,0),(1,0),(1,1).

8. KPB 8
Fluks Medan Vektor
menembus Permukaan Dua Sisi
Teorema
Andaikan G permukaan dua sisi yang diberikan oleh ( , )z f x y= at au
( , , ) ( , ) ,( , )F x y z z f x y x y R= − ∈ (R=proyeksi G pada XOY)
Jika n
r
vektor normal satuan arah ke atas pada G, dan F Mi Nj Pk= + +
rr r r
suatu medan vektor, maka fluks yang melintasi G adalah :
( ). x y
G R
fluks F F n dS Mf Nf P dA= = − − +∫∫ ∫∫
r r

9. KPB 9
x
y
z
G
R
n
r
F
r
( ). .
G G
F
F n dS Mi Nj Pk dS
F
 ∇
= + +  ÷ ÷∇ 
∫∫ ∫∫
rr r rr
( ) 2 2
.
1
x y
G x y
f i f j k
Mi Nj Pk dS
f f
 − − +
 ÷= + +
 ÷+ + 
∫∫
rr r
rr r
( ) 2 2
2 2
1
. 1
1
x y x y
R x y
Mf Nf P f f dA
f f
 
 ÷= − − + + +
 ÷+ + 
∫∫
( ). x y
G R
fluks F F n dS Mf Nf P dA= = − − +∫∫ ∫∫
r r
Sehingga
Bukti:

10. KPB 10
Contoh:
Hitung fluks untuk medan vektor F xi yj zk= + +
rr r r
yang melintasi bagian G
dari paraboloid 2 2
1z x y= − − yang terletak di atas bidang xy, dengan
n
r
berupa normal ke atas.
Jawab: 2 2
1 2 , 2x yz x y f x f y= − − → = − = −
( ). x y
G R
fluks F F n dS Mf Nf P dA= = − − +∫∫ ∫∫
r r
R= lingkaran satuan
( )2 2
2 2
R
x y z dA= + +∫∫ ( )2 2
1
R
x y dA= + +∫∫
2 1
2
0 0
(1 )r r drd
π
θ= +∫ ∫
2
2 4
0
1 21 1 3 3
.
0 02 4 4 2
r r d
π
π
θ θ π= + = =∫

11. KPB 11
Latihan
Hitung fluks F yang melintasi G untuk tiap hal berikut:
1. ; bagian bidang 8 4 5F yi xj G z x y= − + = − −
r r r
di atas segitiga dengan
titik sudut (0,0,0),(0,1,0),(1,0,0).
2
2. 9 ; bagian bidang 2 3 6 6F x j G x y z= − + + =
r r
di oktan pertama.
3. 2 ;F yi xj k= − +
rr r r
G permukaan yang ditentukan oleh
2
1 ,z y= −
0 5.x≤ ≤

12. KPB 12
Teorema Divergensi Gauss
Misalkan F Mi Nj Pk= + +
rr r r
medan vektor sehingga M,N,P
mempunyai turunan pertama yang kontinu pada benda pejal S,
dan permukaan S∂ adalah batas S.
Jika n
r
menyataka vektor normal satuan arah ke luar terhadap ,S∂
maka,
.
S S S
M N P
F n dS divF dV dV
x y z∂
 ∂ ∂ ∂
= = + + ÷
∂ ∂ ∂ 
∫∫ ∫∫∫ ∫∫∫
r rr
Artinya; Fuks F yang melewati batas suatu daerah tertutup di ruang
=integral lipat tiga dari divergensi F atas daerah tersebut.

13. KPB 13
Contoh :
Hitung fluks medan vektor 2 3
2F x yi xzj yz k= + +
rr r r
melewati
permukaan benda pejal persegipanjang S ;
{ }( , , ) | 0 1,0 2,0 3S x y z x y z= ≤ ≤ ≤ ≤ ≤ ≤
a. secara langsung
b. dengan teorema Gauss
x
y
z
Sisi x = 1 
2
. .n i F n x y F n y= → = → =
r rrr r r
3 2
1 0 0
. 6
x
F n dS ydydz
=
= =∫∫ ∫∫
r r
a. hitung .
S
F ndS
∂
∫∫
r r
atas keenam sisi balok

14. KPB 14
Dengan cara yang sama dihitung untuk lima sisi lainnya , hasilnya :
Sisi n F.n
x = 1 i y 6
x = 0 -i 0 0
y = 2 j 2xz 18
y = 0 -j -2xz -18
z = 3 k 27y 54
z= 0 -k 0 0
.
S
F ndS
∂
∫∫
r r
Jadi, . 6 0 18 18 54 0 60.
S
F ndS
∂
= + + − + + =∫∫
r r

15. KPB 15
b. dengan teorema Gauss
2
. (2 0 3 )
S S
F ndS xy yz dV
∂
= + +∫∫ ∫∫∫
r r
1 2 3
2
0 0 0
(2 3 )xy yz dzdydx= +∫∫∫
1 2
0 0
(6 27 )xy y dydx= +∫∫
1
2
0
1
(12 54) 6 54 60.
0
x dx x x= + = + =∫
.
S S
M N P
F n dS dV
x y z∂
 ∂ ∂ ∂
= + + ÷
∂ ∂ ∂ 
∫∫ ∫∫∫
r r 2 3
; 2F x yi xzj yz k= + +
rr r r

16. KPB 16
Latihan
Gunakan teorema divergensi Gauss untuk menghitung .
S
F ndS
∂
∫∫
r r
2 2
1. ; :0 9F zi xj yk S z x y= + + ≤ ≤ − −
rr r r
2. 2 3 ; :0 1,0 1,0 1F xi yj zk S x y z= + + ≤ ≤ ≤ ≤ ≤ ≤
rr r r
2 2 2
3. 3 2 4 ; bola 9F xi yj zk S x y z= − + + + ≤
rr r r
2 2 2 2 2
4. ; :0 4F x i y j z k S z x y= + + ≤ ≤ − −
rr r r

17. KPB 17
Teorema Stokes
Andaikan S permukaan dua sisi dan batas S (adalah S∂ ) berupa
kurva tertutup sederhana. F Mi Nj Pk= + +
rr r r
medan vektor sehingga
M,N,P mempunyai turunan parsial pertama yang kontinu pada S dan S∂
n
r
vektor normal satuan, T
r
vektor singgung satuan terhadap ,S∂
maka
. .
S S
F T dS curl F n dS
∂
=∫ ∫∫
r r r r
Ñ
Catatan: jika kita bergerak sepanjang ,S∂ n
r
menyatakan arah kepala, maka S berada di sebelah kiri.
dengan

18. KPB 18
Contoh:
Hitung . , ( ) ( ) ( )
C
F T dS F y x i x z j x y k= − + − + −∫
rr r r r r
Ñ
C adalah batas S : 2 2x y z+ + = di oktan pertama, terarah sesuai
putaran jarum jam jika dipandang dari atas.
Jawab
x
y
z
n
r
( )* * *
. . x y
C S R
F T dS curl F n dS M f N f P dA= = − − +∫ ∫∫ ∫∫
r r r r
Ñ
S C∂ =

19. KPB 19
( 1 1) (1 0) (1 1)
i j k
curl F i j k j
x y z
y x x z x y
∂ ∂ ∂
= = − + − − + − = −
∂ ∂ ∂
− − −
rr r
rr r r r
Bidang S: 2 2 1 , 2x yz x y f f= − − → = − = −
Proyeksi S pada XOY:
{ }( , ) | 0 2 2 ,0 1R x y x y y= ≤ ≤ − ≤ ≤
1
2
x
y

20. KPB 20
( )* * *
. . x y
C S R
F T dS curl F n dS M f N f P dA= = − − +∫ ∫∫ ∫∫
r r r r
Ñ
( )( 0)( 1) ( 1)( 2) 0
R
dA= − − − − − − +∫∫
Dari * * *
curl F j M i N j P k= − = + +
rr r r r
2 21 1
0 0 0
2 2
2 2
0
y
y
dxdy x
−
−
= − − =∫ ∫ ∫
1
2
0
1
4 4 4 2 2.
0
y dy y y= − = − =∫
n
r
arah bawah

21. KPB 21
Latihan
A. Hitung dengan teorema Stokes .
S
curl F n dS∫∫
r r
2 2 2
1.F x i y j z k= + +
rr r r
,S adalah belahan bola
2 2
1z x y= − −
dan n
r
normal arah atas.
2
2. 3F yzi xzj z k= + +
rr r r
,S adalah bagian bola
2 2 2
16x y z+ + =
dibawah bidang z = 2.
3. 4 2 3F yi zj xk= − + +
rr r r
,S adalah bagian dari paraboloida elips
2 2
10z x y= − − diatas bidang z = 1.
B. Hitung . ,
C
F T dS∫
r r
Ñ C adalah elips yang merupakan perpotongan bidang
z x= dan tabung 2 2
4,x y+ = terarah sesuai putaran jarum jam dari atas.
2 3F zi xj yk= + +
rr r r