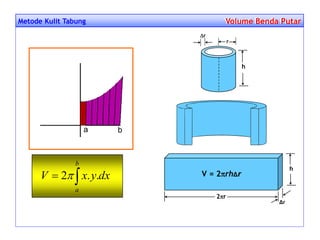
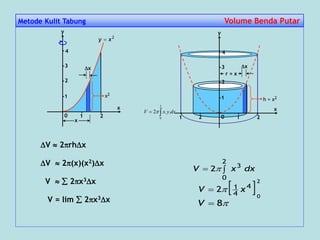
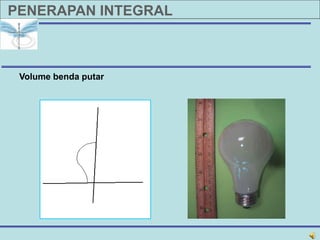
Dokumen tersebut membahas tentang penggunaan integral untuk menghitung luas daerah dan volume benda dengan menjelaskan langkah-langkah penyelesaiannya seperti partisi, aproksimasi luas, jumlahkan, ambil limit, dan integralkan. Contoh soal dan penyelesaiannya juga diberikan untuk memperjelas penjelasan tentang penggunaan integral."

1. APLIKASI INTEGRAL
Ida Mariati Hutabarat

2. Pendahuluan Penggunaan Integral
Pilar-pilar jembatan pada gambar di atas
membentuk partisi-partisi yang akan kita temukan
dalam pokok bahasan menghitung luas daerah
dengan menggunakan integral.

3. =
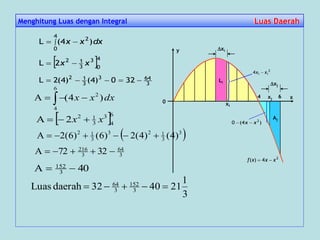
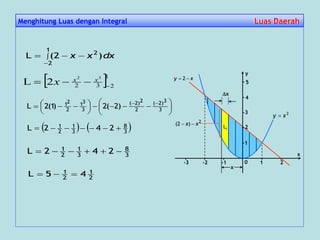
= 2(2)3 – 2(2)2 – [2(-1)3 – 2(-1)2]
= 16 – 8 + 2 + 2 = 12
 


2
1
2
dx46 xx  2
1
23
22  xx
Integral Tentu Luas DaerahLuas Daerah
Hitunglah nilai dari  


2
1
2
dx46 xx
Contoh 1 :
Jawab
Misalkan f adalah fungsi yang kontinyu pada selang [a, b] dan
misalkan F adalah anti turunan dari f pada selang tersebut, maka
berlaku :
Untuk meringkas penulisan, F(b) – F(a) dinotasikan sebagai
Teorema Dasar Kalkulus
)(F)(F)( abdxxf
b
a

 b
ax)(F

4. Secara geometri definisi integral Riemaan di atas dapat diartikan sebagai
luas daerah di bawah kurva y = f(x) pada interval [a, b].
y
x
0 a bx
y
a
x
0 b

b
a
dxxf )(
Jumlah Luas Partisi Berubah Menjadi Integral
Tentukan limitnya
n  
)(xf


n
i
ii xxf
1
)( 
)(xf
Menghitung Luas dengan Integral Luas DaerahLuas Daerah
i
n
i
i
n
b
a
xxfdxxfL  
 1
)()( lim

5. Kegiatan pokok dalam menghitung luas
daerah dengan integral tentu adalah:
1. Gambar daerahnya.
2. Partisi daerahnya
3. Aproksimasi luas sebuah partisi
Li  f(xi) xi
4. Jumlahkan luas partisi
L   f(xi) xi
5. Ambil limitnya L = lim  f(xi) xi
6. Nyatakan dalam integral
x
0
y
)(xfy 
a
xi
xi
)( ixf
Li
Menghitung Luas dengan Integral Luas DaerahLuas Daerah

a
dxxf
0
)(L

6. Hitunglah luas daerah tertutup yang dibatasi kurva y = x2, sumbu x, dan garis x = 3
Contoh 1.
Langkah penyelesaian :
1. Gambarlah daerahnya
2. Partisi daerahnya
3. Aproksimasi luasnya Li  xi
2 xi
4. Jumlahkan luasnya L   xi
2 xi
5. Ambil limit jumlah luasnya
L = lim  xi
2 xi
6. Nyatakan dalam integral dan
hitung nilainya
y
0
x
3
2
)( xxf 
dxx
3
0
2
L
903
33
3
0
3
3
L 



 x
Li
xi
xi
2
ix
Menghitung Luas dengan Integral Luas DaerahLuas Daerah
Jawab

7. Hitunglah luas daerah tertutup yang dibatasi kurva y = x2, sumbu Y, dan garis y = 4
Contoh 2.
Langkah penyelesaian :
1. Gambarlah daerahnya
2. Partisi daerahnya
3. Aproksimasi luasnya L  xi.y
4. Jumlahkan luasnya L   y. y
5. Ambil limit jumlah luasnya
L = lim  y. y
6. Nyatakan dalam integral dan
hitung nilainya
y
0
x
4
dyy
4
0
.L
3
16
8.
3
2
3
2
L
4
0
2
3






 y
Menghitung Luas dengan Integral Luas DaerahLuas Daerah
Jawab
xi
2
)( xxf 
y
y

8. Langkah penyelesaian:
1. Gambar dan Partisi daerahnya
2. Aproksimasi : Li  (4xi - xi
2)xi dan
Aj  -(4xj - xj
2)xj
3. Jumlahkan : L  (4xi - xi
2)xi dan A
  -(4xj - xj
2)xj
4. Ambil limitnya L = lim  (4xi - xi
2)xi
dan A = lim  -(4xj - xj
2)xj
5. Nyatakan dalam integral
6. dan
y
0
x64
2
4)( xxxf 
dx)xx4(
4
0
2
 L dxxx 
6
4
2
)4(A
xi
Li
xi
xj
Aj
xj
2
4 ii xx 
)4(0 2
xx 
Menghitung Luas dengan Integral Luas DaerahLuas Daerah
Hitunglah luas daerah tertutup yang dibatasi kurva y = 4x - x2, sumbu x,
dan garis x = 6
Contoh 3.
Jawab

9. dxxx 
4
0
2
)4(L
dxxx 
6
4
2
)4(A
y
0
x64
2
4)( xxxf 
xi
Li
xi
xj
Aj
xj
2
4 ii xx 
)4(0 2
xx 
 4
0
3
3
12
2L xx 
3
643
3
12
320)4()4(2L 
 6
4
3
3
12
2A xx 
 3
3
123
3
12
)4()4(2)6()6(2A 
3
64
3
216
3272A 
40A 3
152

3
1
214032daerahLuas 3
152
3
64

Menghitung Luas dengan Integral Luas DaerahLuas Daerah

10. Menghitung Luas dengan Integral Luas DaerahLuas Daerah
Kesimpulan :

b
a
dyxL .
b
a
dxyL .
y
0
x
y
y
x
0
)(xfy xi
xi
)( ixf
y

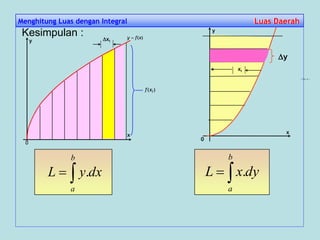
11. LUAS DAERAH ANTARA DUA KURVA
Perhatikan kurva y = f(x) dan y = g(x) dengan f(x) > g(x) pada selang
[a, b] di bawah ini. Dengan menggunakan cara : partisi, aproksimasi,
jumlahkan, ambil limitnya, integralkan, maka dapat ditentukan luas
daerah antara dua kurva tersebut.
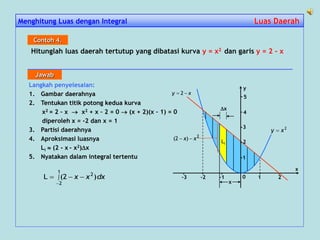
Langkah penyelesaian:
1. Gambar daerahnya
2. Partisi daerahnya
3. Aproksimasi : Li  [ f(x) – g(x) ] x
4. Jumlahkan : L   [ f(x) – g(x) ] x
5. Ambil limitnya :
L = lim  [ f(x) – g(x) ] x
6. Nyatakan dalam integral tertentu
y
ba
)(xfy 
)(xgy 
0
x
Li
x
x
)()( xgxf 
Menghitung Luas dengan Integral Luas DaerahLuas Daerah
 dxxgxf
b
a
  )()(L

12. Hitunglah luas daerah tertutup yang dibatasi kurva y = x2 dan garis y = 2 - x
Contoh 4.
Langkah penyelesaian:
1. Gambar daerahnya
2. Tentukan titik potong kedua kurva
x2 = 2 – x  x2 + x – 2 = 0  (x + 2)(x – 1) = 0
diperoleh x = -2 dan x = 1
3. Partisi daerahnya
4. Aproksimasi luasnya
Li  (2 - x - x2)x
5. Nyatakan dalam integral tertentu
dxxx


1
2
2
)2(L 0
x
1 2-1-2-3
2
xy 
xy  2
y
1
2
3
4
5
Li
x
x
2
)2( xx 
Menghitung Luas dengan Integral Luas DaerahLuas Daerah
Jawab

13. dxxx


1
2
2
)2(L
0
x
1 2-1-2-3
2
xy 
xy  2
y
1
2
3
4
5
Li
x
x
2
)2( xx 
 1
232
32
2L 
 xx
x










 

3
3)2(
2
2)2(
3
31
2
21
)2(2)1(2L
   3
8
3
1
2
1
242L 
3
8
3
1
2
1
242L 
2
1
2
1
45L 
Menghitung Luas dengan Integral Luas DaerahLuas Daerah

14. Untuk kasus tertentu pemartisian
secara vertikal menyebabkan ada
dua bentuk integral. Akibatnya
diperlukan waktu lebih lama untuk
menghitungnya.
)(xfy 
y
a b
Lix
x
)()( xgxf 
)(2 xf
Ai
0
x
)(xgy 
Luas daerah = 
a
dxxf
0
)(2   
b
a
dxxgxf )()(
Menghitung Luas dengan Integral Luas DaerahLuas Daerah

15. Jika daerah tersebut dipartisi secara horisontal, maka akan diperoleh
satu bentuk integral yang menyatakan luas daerah tersebut. Sehingga
penyelesaiannya menjadi lebih sederhana dari sebelumnya.
)()( yfxxfy 
y
0
x
)()( ygxxgy 
Luas daerah =   
d
c
dyyfyg )()(
Li y
c
d
)()( yfyg 
Menghitung Luas dengan Integral Luas DaerahLuas Daerah

16. Hitunglah luas daerah di kuadran I yang dibatasi kurva y2 = x, garis x + y = 6,
dan sumbu x
Contoh 5.
Langkah penyelesaian:
1. Gambar daerahnya
2. Tentukan titik potong kedua kurva
y2 = 6 – y  y2 + y – 6 = 0  (y + 3)(y – 2) = 0
diperoleh y = - 3 dan y = 2
3. Partisi daerahnya
4. Aproksimasi luasnya
Li  (6 - y - y2)y
5. Nyatakan dalam integral tertentu
Luas daerah =   
2
0
2
6 dyyy
2
yx 
yx  6
2
y
6
x
0
6
Li
y
y
2
)6( yy 
Menghitung Luas dengan Integral Luas DaerahLuas Daerah
Jawab

17. Luas daerah =   
2
0
2
6 dyyy
2
yx 
yx  6
2
y
6
x
0
6
Li y
y
2
)6( yy 
Luas daerah =
2
0
3
3
2
2
6









yy
y
Luas daerah = 0
3
32
2
4)2(6 








Luas daerah = 




 
3
8212
Luas daerah = 3
22
Menghitung Luas dengan Integral Luas DaerahLuas Daerah

18. PENERAPAN INTEGRAL
Volume benda putar

19. Pendahuluan Volume Benda PutarVolume Benda Putar
Suatu daerah jika di putar
mengelilingi garis tertentu sejauh
360º, maka akan terbentuk suatu
benda putar. Kegiatan pokok dalam
menghitung volume benda putar
dengan integral adalah: partisi,
aproksimasi, penjumlahan,
pengambilan limit, dan menyatakan
dalam integral tentu. Gb. 4

20. Pendahuluan Volume Benda PutarVolume Benda Putar
Dalam menentukan volume benda putar yang harus diperhatikan adalah
bagaimana bentuk sebuah partisi jika diputar. Berdasarkan bentuk partisi
tersebut, maka metode yang digunakan untuk menentukan volume benda
putar dibagi menjadi :
1. Metode cakram
2. Metode cincin
3. Metode kulit tabung
y
0 x
y
x
0
x
1 2-
2
-
1
y
1
2
3
4

21. Metode Cakram Volume Benda PutarVolume Benda Putar
Metode cakram yang digunakan dalam
menentukan volume benda putar dapat
dianalogikan seperti menentukan volume
mentimun dengan memotong-motongnya
sehingga tiap potongan berbentuk cakram.

22. Metode Cakram Volume Benda PutarVolume Benda Putar
Bentuk cakram di samping dapat
dianggap sebagai tabung dengan jari-jari
r = f(x), tinggi h = x. Sehingga
volumenya dapat diaproksimasi sebagai
V  r2h atau V   f(x)2x.
Dengan cara jumlahkan, ambil
limitnya, dan nyatakan dalam integral
diperoleh:
V    f(x)2 x
V = lim   f(x)2 x
dxxf
a

0
2)]([v 
x
h=x
x
x
y
0 x
y
x
a
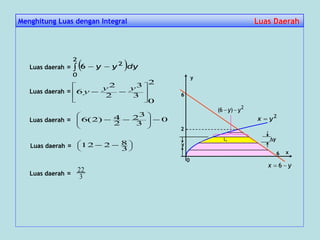
)(xf
)(xfr 
dxy
a

0
2
V 

23. Metode Cakram Volume Benda PutarVolume Benda Putar
x
h=x
x
x
y
0 x
y
x
a
)(xf
)(xfr 
dxy
a
.V
0
2
 
x
h=y
)(yfxr 
y
y
y
x
)()( yfxxfy 
x
y
)(xfy 
dyx
a

0
2
.V 

24. Metode Cakram Volume Benda PutarVolume Benda Putar
Hitunglah volume benda putar yang terjadi jika daerah yang dibatasi kurva y = x2 + 1,
sumbu x, sumbu y, garis x = 2 diputar mengelilingi sumbu x sejauh 360º.
Contoh 6.
Langkah penyelesaian:
1. Gambarlah daerahnya
2. Buat sebuah partisi
3. Tentukan ukuran dan
bentuk partisi
4. Nyatakan dalam bentuk
integral.
y
2x
12
x
x
12
 xy
1
y
h=x
x
x
12
 xr
x
Jawab
dxyV 
2
0
.
2

dxxV  
2
0
22
)1(

25. Metode Cakram Volume Benda PutarVolume Benda Putar
y
h=x
x
x
12
 xr
dxxV  
2
0
22
)1(
dxxxV  
2
0
24
)12(
 2
0
3
3
25
5
1 xxxV  
 15
11
3
16
5
32 13)02( V
dxyV 
2
0
.
2


26. Metode Cakram Volume Benda PutarVolume Benda Putar
Hitunglah volume benda putar yang terjadi jika daerah yang dibatasi kurva y = x2,
sumbu y, garis y = 2 diputar mengelilingi sumbu y sejauh 360º.
Contoh 7.
Langkah penyelesaian:
1. Gambarlah daerahnya
2. Buatlah sebuah partisi
3. Tentukan ukuran dan bentuk
partisi
4. Aproksimasi volume partisi yang
diputar, jumlahkan, ambil
limitnya, dan nyatakan dalam
bentuk integral.
2
y
y
2
xy 
x
y
y
x
y
h=y
y
yr 
Jawab

27. Metode Cakram Volume Benda PutarVolume Benda Putar
  dy
2
0
yV  2

 2
0
2
2
1
yV 
)04(2
1
 V
x
y
h=y
y
yr 
2
dyyV 
2
0

2V
   dy
2
0
2
yfV   y = x2

28. Metode Cincin Volume Benda PutarVolume Benda Putar
Metode cincin yang digunakan dalam
menentukan volume benda putar
dapat dianalogikan seperti
menentukan volume bawang bombay
dengan memotong-motongnya yang
potongannya berbentuk cincin.

29. Metode Cincin Volume Benda PutarVolume Benda Putar
Menghitung volume benda putar
dengan menggunakan metode
cincin dilakukan dengan
memanfaatkan rumus volume
cincin seperti gambar di samping,
yaitu V= (R2 – r2)h
h
r
R
dan  
b
a
dxyyV .
2
2
2
1   
b
a
dyxxV .
2
2
2
1

30. Metode Cincin Volume Benda PutarVolume Benda Putar
Hitunglah volume benda putar yang terjadi jika daerah yang dibatasi kurva
y = x2 dan garis y = 2x diputar mengelilingi sumbu x sejauh 360º.
Contoh 8.
Langkah penyelesaian:
1. Gambarlah daerahnya
2. Buat sebuah partisi
3. Tentukan ukuran dan
bentuk partisi
4. Aproksimasi volume partisi
yang diputar, jumlahkan,
ambil limitnya, dan
nyatakan dalam bentuk
integral.
4
y
y = 2x
2
2
xy 
x
x
x
x2
2x
y
x
Jawab

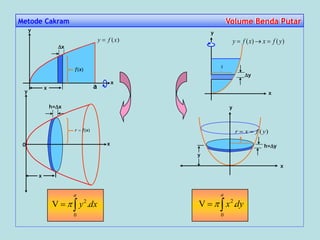
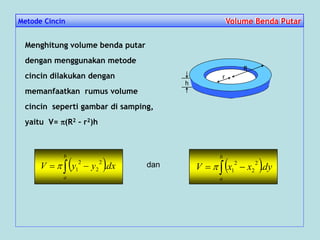
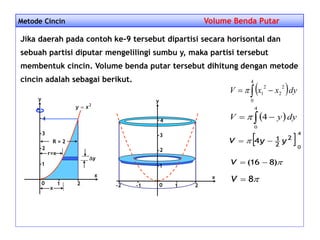
31. Metode Cincin Volume Benda PutarVolume Benda Putar
y
x
4
y
y = 2x
2
2
xy 
x
x
x
r=x2
R=2x
V  (R2 – r2) h
V   [ (2x)2 – (x2)2 ] x
dxxxV  
2
0
42 )4(
 2
0
5
5
13
3
4 xxV  
)(
5
32
3
32  V
)(
15
96160 V
15
64V
dxyyV  
2
0
2
2
2
1 )(

32. Metode Kulit Tabung Volume Benda PutarVolume Benda Putar
Metode kulit tabung yang digunakan
untuk menentukan volume benda putar
dapat dianalogikan seperti menentukan
volume roti pada gambar disamping.

33. Metode Kulit Tabung Volume Benda PutarVolume Benda Putar
r
r
h
h
2r
Δr
V = 2rhΔr
a b

b
a
dxyxV ..2

34. Metode Kulit Tabung Volume Benda PutarVolume Benda Putar
Hitunglah volume benda putar yang terjadi jika daerah yang dibatasi kurva
y = x2 , garis x = 2, dan sumbu x diputar mengelilingi sumbu y sejauh 360º.
Contoh 9.
Langkah penyelesaian:
1. Gambarlah daerahnya
2. Buatlah sebuah partisi
3. Tentukan ukuran dan bentuk partisi.
4. Aproksimasi volume partisi yang
diputar, jumlahkan, ambil limitnya,
dan nyatakan dalam bentuk integral. 0
x
1 2
x
x
2
xy 
x2
y
1
2
3
4
Jawab

35. Metode Kulit Tabung Volume Benda Putar
0
x
1 2
x
x
2
xy 
x2
y
1
2
3
4
r = x
x
h = x2
0
x
1 21 2
y
1
2
3
4
V  2rhx
V  2(x)(x2)x
V   2x3x
V = lim  2x3x
dxxV 
2
0
3
2
 
2
0
4
4
12 xV 
8V
dxyxV ..2
2
0
 

36. Metode Cincin Volume Benda Putar
Jika daerah pada contoh ke-9 tersebut dipartisi secara horisontal dan
sebuah partisi diputar mengelilingi sumbu y, maka partisi tersebut
membentuk cincin. Volume benda putar tersebut dihitung dengan metode
cincin adalah sebagai berikut.
0
x
1 2-2 -1
y
1
2
3
4
 dyyV  
4
0
4
 
4
0
2
2
14 yyV  
)816( V
8V0
x
1 2
x
2
xy 
y
1
2
3
4
y
r=x
R = 2
 dyxxV  
4
0
2
2
2
1