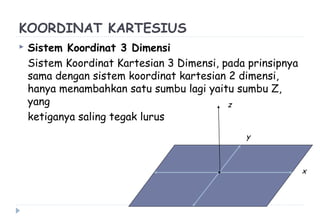
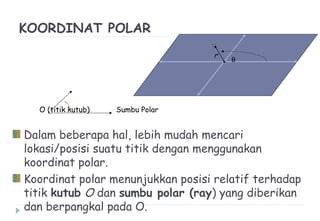
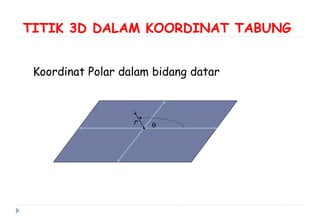
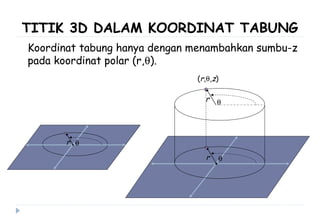
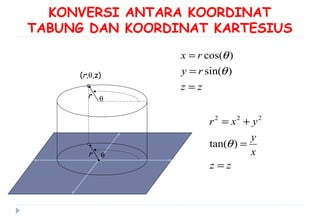
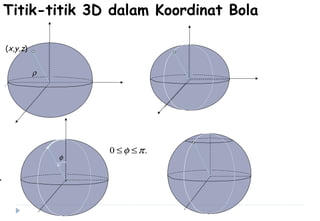
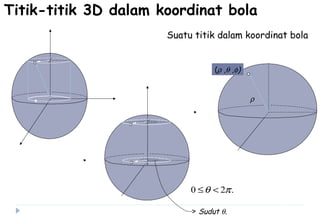
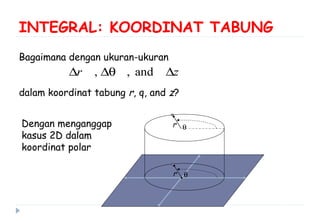
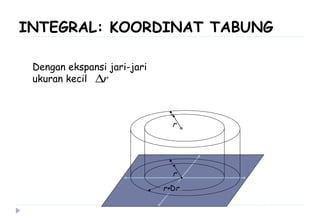
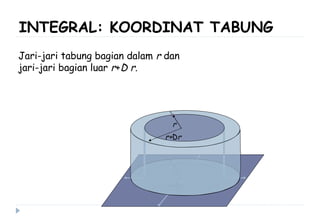
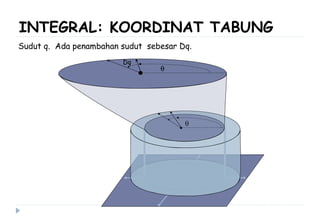
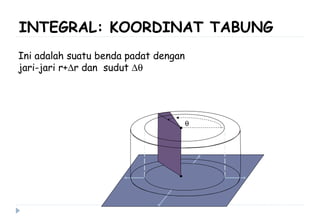
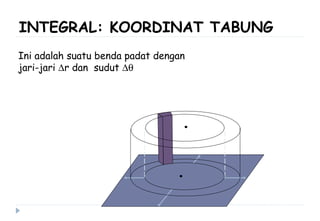
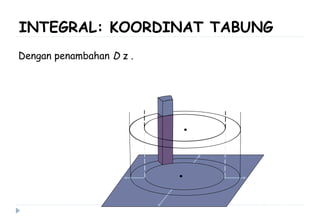
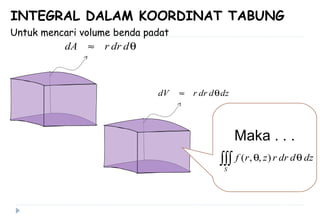
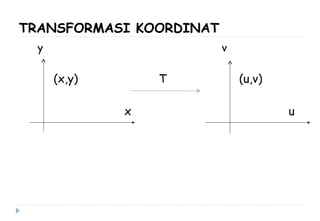
Dokumen ini membahas berbagai sistem koordinat, termasuk koordinat kartesius, polar, tabung, dan bola, serta konversi antar sistem tersebut. Selain itu, dokumen ini mencakup integral lipat dan transformasi koordinat dengan penjelasan mengenai penggunaan jacobian untuk menghitung perubahan variabel dalam integral. Terdapat juga contoh soal yang menjelaskan penerapan konsep tersebut dalam menghitung volume dan menggambarkan persamaan dalam berbagai sistem koordinat.

1. Koordinat Kartesius, Koordinat Tabung
& Koordinat Bola
Editing by
Wiwik Andriyani L N/2KS-1

2. KOORDINAT KARTESIUS
 Sistem Koordinat 2 Dimensi
Sistem koordinat kartesian dua dimensi merupakan
sistem koordinat yang terdiri dari dua sumbu yang
saling tegak lurus, biasanya sumbu
X dan Y
x
y

3. KOORDINAT KARTESIUS
 Sistem Koordinat 3 Dimensi
Sistem Koordinat Kartesian 3 Dimensi, pada prinsipnya
sama dengan sistem koordinat kartesian 2 dimensi,
hanya menambahkan satu sumbu lagi yaitu sumbu Z,
yang
ketiganya saling tegak lurus
x
y
z

4. KOORDINAT POLAR
• Dalam koordinat polar, koordinat suatu titik didefinisikan
fungsi dari arah dan jarak dari titik ikatnya.
• Jika O merupakan titik pusat koordinat dan garis OX
merupakan sumbu axis polar, maka titik P dapat ditentukan
koordinatnya dalam sistem koordinat polar berdasarkan
sudut vektor (θ) dan radius vektor (r) atau (garis OP) yaitu
P (r, θ). Sudut vektor (θ) bernilai positif jika mempunyai
arah berlawanan dengan arah putaran jarum jam, sedangkan
bernilai negatif jika searah dengan putaran jarum jam.

5. KOORDINAT POLAR
O (titik kutub) Sumbu Polar
Dalam beberapa hal, lebih mudah mencari
lokasi/posisi suatu titik dengan menggunakan
koordinat polar.
Koordinat polar menunjukkan posisi relatif terhadap
titik kutub O dan sumbu polar (ray) yang diberikan
dan berpangkal pada O.
r
θ

6. Titik P dengan koordinat polar (r, θ) berarti berada
diposisi:
- θ derajat dari sumbu-x (sb. polar)
(θ diukur berlawanan arah jarum-jam)
- berjarak sejauh r dari titik asal kutub O.
Perhatian:
jika r < 0, maka P berada di posisi yang
berlawanan arah.
r: koordinat radial
θ: koordinat sudut

7. Setiap titik mempunyai lebih dari satu representasi dalam
koordinat polar
(r, θ) = (- r, θ + nπ ), untuk n bil. bulat ganjil
= ( r, θ + nπ ), untuk n bil. Bulat genap
Contoh:
Nyatakan koordinat polar berikut ke dalam
bentuk koordinat kartesius.
(2, π/3), (-2, 4π/3), (2, 7π/3), (-2, -2π/3).

8. Konversi koordinat polar kedalam koordinat tegak.
Gunakan relasi:
x = r cos θ , y = r sin θ
Maka r2
= x2
+ y2
,
tan θ = y/x, jika x ≠ 0
Catt. menentukan θ
Jika x >0, maka x berada di kuadran 1 atau 4
jadi -π/2 < θ < π/2  θ = arctan(y/x).
Jika x < 0, x berada di kuadran 2 atau 3,
θ = π + arctan(y/x).

9. KOORDINAT POLAR
 Pers. polar dari lingkaran berjari-jari a: r = a
 Contoh: Untuk lingkaran berjari a,
- berpusat di (0,a): r = 2a sin θ
- berpusat di (a,0): r = 2a cos θ
Jika a=1, maka
r = 2 sin θ
r = 2 cos θ

10. Konversikan persamaan polar r = 2 sin θ kedalam sistem
koordinat tegak:
Kalikan kedua sisi dengan r:
r2 = 2r sin θ
x2 + y2 = 2y
x2 + y2 - 2y = 0
Jadi persamaan tsb. dalam koordinat tegak adalah x2 + (y
-1)2 = 1

11. TITIK 3D DALAM KOORDINAT TABUNG
θr
Koordinat Polar dalam bidang datar

12. Koordinat tabung hanya dengan menambahkan sumbu-z
pada koordinat polar (r,θ).
θr
θr
θr
(r,θ,z)
TITIK 3D DALAM KOORDINAT TABUNG

13. KONVERSI ANTARA KOORDINAT
TABUNG DAN KOORDINAT KARTESIUS
cos( )
sin( )
x r
y r
z z
θ
θ
=
=
=
θr
θr
(r,θ,z)
2 2 2
tan( )
r x y
y
x
z z
= +
=
=
θ

14. Titik-titik 3D dalam Koordinat Bola
(x,y,z)
ρ
0 .φ π≤ ≤
φ

15. Titik-titik 3D dalam koordinat bola
Sudut θ.
0 2 .θ π≤ <
(ρ ,θ ,φ)
ρ
Suatu titik dalam koordinat bola

16. KONVERSI ANTARA KOORDINAT BOLA
DAN KOORDINAT KARTESIUS
φ
(x,y,z)
z
ρ
r
sin( ) cos( ) tan( )
r z r
z
φ φ φ
ρ ρ
= = =
cos( ) sin( )cos( )
sin( ) sin( )sin( )
cos( )
x r
y r
z
θ ρ φ θ
θ ρ φ θ
ρ φ
= =
= =
=
2 2 2
2 2
2 2 2
tan( )
tan( )
cos( )
x y z
y
x
x yr
z z
z z
x y z
ρ
θ
φ
φ
ρ
= + +
=
+
= =
= =
+ +

17. INTEGRAL: KOORDINAT KARTESIUS
Riemann Sum dalam triple integral sbb:
Untuk menghitung volume balok-balok kecil
dengan ukuran panjang . , lebar , dan
tinggi
* * *
( , , ) .i i i i i if x y z x y z∆ ∆ ∆
* * *
( , , ) .i i i i i i
nilai fungsi pada volumebalok kecil
titik tertentu
f x y z x y z∆ ∆ ∆
14243 14243
ix∆ iy∆
iz∆

18. INTEGRAL: KOORDINAT TABUNG
Bagaimana dengan ukuran-ukuran
dalam koordinat tabung r, q, and z?
, , andr z∆ ∆θ ∆
Dengan menganggap
kasus 2D dalam
koordinat polar
θr
θr

19. INTEGRAL: KOORDINAT TABUNG
Dengan ekspansi jari-jari
ukuran kecil r∆
r
r+Dr
r

20. INTEGRAL: KOORDINAT TABUNG
r+Dr
r
Jari-jari tabung bagian dalam r dan
jari-jari bagian luar r+D r.
r
r+Dr

21. INTEGRAL: KOORDINAT TABUNG
Sudut q. Ada penambahan sudut sebesar Dq.
θ
θ
Dq

22. INTEGRAL: KOORDINAT TABUNG
θ
Ini adalah suatu benda padat dengan
jari-jari r+∆r dan sudut ∆θ

23. INTEGRAL: KOORDINAT TABUNG
Ini adalah suatu benda padat dengan
jari-jari ∆r dan sudut ∆θ

24. INTEGRAL: KOORDINAT TABUNG
Dengan penambahan D z .

25. INTEGRAL DALAM KOORDINAT TABUNG
dA r dr d≈ θ
Untuk mencari volume benda padat
dV r dr d dz≈ θ
Maka . . .
( , , )
S
f r z r dr d dzθ θ∫∫∫

26. SOAL
1. Hitunglah dimana S
tetrahedron dengan titik-titik sudut (0,0,0),
(3,2,0), (0,3,0), dan (0,0,2).
x y z
S
e dV+ +
∫∫∫

27. SOAL
2. Diketahui persamaan dalam
koordinat tabung:
a.
b.
Tentukan persamaan dalam
koordinat kartesius & gambarkan
2 2
9r z+ =
2 cos 3 sin 6r r zθ θ− + =

28. SOAL
3. Diketahui persamaan dalam koordinat
kartesius:
a.
b.
Tentukan persamaan dalam
koordinat tabung & gambarkan
2 2
9x y+ =
2 2 2
2 12 14 0x y z z+ + − + =

29. SOAL
4. Diketahui persamaan dalam koordinat bola:
a.
b.
c.
Tentukan persamaan dalam
koordinat kartesius & gambarkan
3ρ =
3
π
θ =
4
π
φ =

30. SOAL
5. Diketahui persamaan dalam koordinat kartesius:
a.
b.
Tentukan persamaan dalam
koordinat bola & gambarkan
2 2 2
4x y z+ + =
2 2 2
1x y z− − =

31. TRANSFORMASI KOORDINAT &
PERUBAHAN VARIABEL PADA INTEGRAL
LIPAT
Editing by
Wiwik Andriyani Lestari Ningsih/2KS-1

32. TRANSFORMASI KOORDINAT
 Dalam menyelesaikan integral lipat atas suatu daerah
R, dapat diselesaikan dengan menggunakan koordinat
lain selain dengan menggunakan koordinat persegi
panjang xy.
 Transformasi dari satu koordinat persegi panjang ke
sistem koordinat lainnya.
32

33. TRANSFORMASI KOORDINAT
 Tinjau suatu fungsi T, yang mempunyai domain D
(daerah pada bidang xy) dan mempunyai range E
(daerah pada bidang uv), sehingga T(x,y)=(u,v).
 T  transformasi koordinat dari bidang xy ke bidang
uv.
 u dan v adalah fungsi dari x dan y
EvuDyxyxgvyxfu ∈∈== ),(,),();,(),,(

34. TRANSFORMASI KOORDINAT
y v
(x,y) T (u,v)
x u

35. CONTOH
 T suatu transformasi koordinat yang didefinisikansbb:
u=x+2y , v=x-2y. (T(x,y))
a. Tentukan nilai untuk (0,1),(1,2) dan (2,-3)
b. Gambarkan pada bidang uv garis vertikal untuk
u=2,u=4,u=6,u=8 dan garis horisontal untuk v=-
1,v=1,v=3,v=5.
c. Gambarkan hubungan kurva u dan kurva v dalam bidang
xy.

36. TRANSFORMASI KOORDINAT
 Jika T suatu transformasi koordinat satu-satu, maka
bisa dicari invers atau transformasi balikannya dari T,
yakni T-1
dari bidang uv ke bidang xy
x = F(u,v) y = G(u,v)
 Jika T suatu transformasi satu-satu maka inversnya T-
1
. Dalam hal ini ,
T-1
(T(x,y)) = (x,y) dan T(T-1
(u,v)) = (u,v)
untuk setiap (x,y) di D dan setiap (u,v) di E.

37. CONTOH
 Tentukan invers dari transformasi T yang didefinisikan
pada contoh sebelumnya.
 Gambarkan kurva pada bidang uv yang memetakan
ellips
atas T-1
14 22
=+ yx

38. PERUBAHAN VARIABEL PADA INTEGRAL LIPAT
 Tinjau untuk suatu daerah R dalam bidang xy,
substitusi x=f(u,v) dan y=g(u,v).
Persamaan ini menyatakan transformasi koordinat W dari
bidang uv ke bidang xy.
Dalam hal ini menentukan daerah S di bidang uv yang
ditransformasi dari R oleh W(menentukan batas integral
baru)
∫∫R
dAyxF ),(
∫∫∫∫ =
SR
dAvugvufFdAyxF )),(),,((),(

39. MATRIKS JACOBIAN
 Jika x=f(u,v) dan y=g(u,v), maka Jacobian dari x dan y
adalah
v
x
u
y
v
y
u
x
v
y
u
y
v
x
u
x
vu
yx
∂
∂
∂
∂
−
∂
∂
∂
∂
=
∂
∂
∂
∂
∂
∂
∂
∂
=
∂
∂
),(
),(

40. CONTOH
 Tentukan jacobian dari
 Jika , tentukan jacobian
),(
),(
vu
yx
∂
∂ vu
euyvex −−
== 22
,
xyvyxu 2,22
=−=
),(
),(
yx
vu
∂
∂

41. THEOREMA
 Jika x=f(u,v) dan y=g(u,v) adalah transformasi
koordinat, maka
Dimana G(u,v) = F{f(u,v),g(u,v)}
∫∫∫∫ ∂
∂
=
SR
dvdu
vu
yx
vuGdydxyxF
),(
),(
),(),(

42. CONTOH
 Hitung untuk daerah R pada bidang
xy yang dibatasi oleh trapezoid dengan titik sudut
(0,1), (0,2), (2,0) dan (1,0).
 Hitung untuk daerah R di kuadran
pertama pada bidang xy antara lingkaran yang berjari-
jari 1 dan berjari-jari 2.
dxdye
R
xyxy
∫∫
+− )/()(
dxdye
R
yx
∫∫
+− )( 22

43.  Transformasi diatas dapat diperluas untuk menyelesaikan
integral lipat tiga. Diberikan transformasi x=f(u,v,w) ,
y=g(u,v,w) , z=h(u,v,w) dari sistem koordinat uvw ke
sistem koordinat xyz.
 Jacobian =
w
z
v
z
u
z
w
y
v
y
u
y
w
x
v
x
u
x
wvu
zyx
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
=
∂
∂
),,(
),,(

44. THEOREMA
 Jika x=f(u,v,w) , y=g(u,v,w) , z=h(u,v,w) transformasi
koordinat, maka
Dimana G(u,v,w)=F{f(u,v,w),g(u,v,w),h(u,v,w)}
∫∫∫∫∫∫ ∂
∂
=
SR
dwdvdu
wvu
zyx
wvuGdzdydxzyxF
),,(
),,(
),,(),,(

45. CONTOH
 Tentukan jacobian dari
x = 2u + 3v – w, y = u – 5w ,z = u + 4w
 Dengan menggunakan koordinat silinder, tentukan
volume benda di atas bidang xy, yang dibatasi oleh
paraboloid dan silinder
),,(
),,(
wvu
zyx
∂
∂
2222
1& yxyxz +=+=

46. CONTOH
 Dengan menggunakan koordinat bola tentukan volume
benda yang bagian atasnya dibatasi oleh
bola dan bagian bawah dibatasi oleh
kerucut
16222
=++ zyx
22
yxz +=