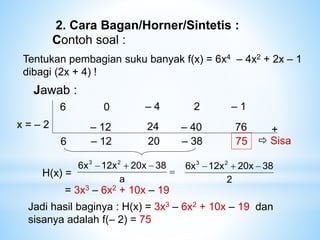
Dokumen ini menjelaskan persamaan kuadrat, cara mengidentifikasi akar-akar, serta metode penyelesaian, termasuk faktorisasi dan rumus kuadrat. Selain itu, diulas juga grafis fungsi kuadrat, sifat akar, dan konsep suku banyak serta teorema sisa untuk pembagian suku banyak. Contoh-contoh soal dan penyelesaian ditambahkan untuk memperjelas penerapan konsep-konsep yang dibahas.

1. VENY TRIYANA ANDIKA SARI, M.Pd.


2. *Persamaan Kuadrat
Definisi :
Persamaan yang berbentuk ax2 + bx + c = 0, dengan
a, b, c ∈ R dan a ≠ 0.
Harga x yang memenuhi persamaan tersebut disebut akar
persamaan kuadrat.
ax2 + bx + c = 0 Persaman Kuadrat
y = ax2 + bx + c Fungsi Kuadrat
ax2 + bx + c Bentuk Kuadrat
Akar Persamaan Kuadrat dapat dicari sebagai berikut:
1. Persamaan Kuadrat Murni
2. Faktorisasi
3. Melengkapkan Kuadrat
4. Rumus Kuadrat
5. Grafik

3. *Persamaan Kuadrat Murni
contoh:
1. 𝑥2
− 4 = 0
maka 𝑥2 = 4 dan akar-akarnya adalah 𝑥 = 2, −2.
2. 2𝑥2
− 21 = 0
maka 𝑥2
= 21/2 dan akar-akarnya adalah
𝑥 = ± 21/2 = ±
1
2
42
*Faktorisasi
𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 0
jika p dan q adalah akar-akar maka 𝑝 + 𝑞 = 𝑏 dan
𝑝 × 𝑞 = 𝑎𝑐

4. contoh :
3. 𝑥2 − 5𝑥 + 6 = 0
(-3)+(-2)= -5 dapat ditulis 𝑥 − 3 𝑥 − 2 = 0
(-3)×(-2)=6
sehingga penyelesaiannya adalah
𝑥 − 3 = 0 dan 𝑥 − 2 = 0
𝑥 = 3 𝑥 = 2
*Melengkapkan Kuadrat
contoh:
4. selesaikan 𝑥2 − 6𝑥 − 2 = 0
langkah 1: ubah bentuk menjadi
𝑥2 − 6𝑥 = 2

5. langkah 2: tambahkan kedua sisi dengan
1
2
𝑏
𝑎
2
= 9
𝑥2
− 6𝑥 + 9 = 2 + 9
𝑥 − 3 2 = 11
𝑥 − 3 = ± 11
𝑥 = 3 ± 11
catatan: 1. koefisien unsur 𝑥2 harus 1 dan
2. bilangan yang ditambahkan kepada kedua sisi
adalah kuadrat dari setengah koefisiean 𝑥.
*Rumus Kuadrat
penyelesaian persamaan kuadrat 𝑎𝑥2
+ 𝑏𝑥 + 𝑐 = 0
diberikan dengan rumus 𝑥 =
−𝑏± 𝑏2−4𝑎𝑐
2𝑎
dimana 𝑏2
− 4𝑎𝑐
disebut diskriminan persamaan kuadrat.

6. *Grafik
akar-akar nyata atau penyelesaian dari 𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 0
adalah harga-harga 𝑥 yang bersesuaian dengan 𝑦 = 0
pada grafik parabola 𝑦 = 𝑎𝑥2
+ 𝑏𝑥 + 𝑐. Jadi penyelesaian
adalah titik potong dengan sumbu absis 𝑥. Apabila grafik
tidak memotong sumbu 𝑥 maka akar-akarnya adalah
khayal.
Sifat-sifat Akar Persamaan Kuadrat
1. Jumlah dan hasil akar-akar
𝑥1 + 𝑥2 =
−𝑏
𝑎
dan 𝑥1. 𝑥2 =
𝑐
𝑎

7. 2. Syarat- syarat utuk kedua akar persamaan kuadrat:
a. Real, jika D ≥ 0 maka:
1) Real berlainan , jika D > 0 maka
• real berlainan tanda: D > 0 dan 𝑥1. 𝑥2 < 0
• real berlawanan: D > 0 dan 𝑥1 + 𝑥2 = 0
2) Real sama, jika D = 0
3) Real positif, jika D ≥ 0, 𝑥1 + 𝑥2 ≥ 0 dan 𝑥1. 𝑥2>0
4) Real negatif, jika D ≥ 0, 𝑥1 + 𝑥2 < 0 dan 𝑥1. 𝑥2 <0
5) Real berkebalikan, jika D ≥ 0 dan 𝑥1. 𝑥2 = 1
b. Imajiner, jika D < 0
c. Jika 𝑥1 = 0 𝑑𝑎𝑛 𝑥2 ≠ 0 maka D >0 dan 𝑥1. 𝑥2 = 0
d. Rasional, jika 𝑎, 𝑏, 𝑐 ∈ 𝑅 serta D merupakan kuadrat
bilangan rasional.

8. *Rumus-rumus lain, sebagai berikut:
a. 𝑥1
2 + 𝑥2
2 = 𝑥1 + 𝑥2
2 − 2𝑥1. 𝑥2
b. 𝑥1 − 𝑥2
2 =
𝑏2−4𝑎𝑐
𝑎2
c. 𝑥1
3
+ 𝑥2
3
= 𝑥1 + 𝑥2
3
− 3𝑥1. 𝑥2 𝑥1 + 𝑥2

9. *
*Fungsi yang berbentuk 𝑥, 𝑦 |𝑦 = 𝑎𝑥2
+ 𝑏𝑥 + 𝑐
dimana 𝑎 ≠ 0 dan 𝑎, 𝑏, 𝑐 ∈ 𝑅
*Harga 𝑥 yang menjadikan 𝑦 = 0 disebut harga
nol dari fungsi tersebut.
*Jadi harga nol dari suatu fungsi adalah akar-
akar persamaan kuadrat 𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 0.
* 𝑥, 𝑦 |𝑦 = 𝑎𝑥2 + 𝑏𝑥 + 𝑐 dapat ditulis dalam
bentuk faktor sebagai berikut:

10. 𝑥, 𝑦 |𝑦 = 𝑎𝑥2 + 𝑏𝑥 + 𝑐
↔ 𝑥, 𝑦 |𝑦 = 𝑎𝑥2 − 𝑎
−𝑏
𝑎
𝑥 +
𝑐
𝑎
𝑎
↔ 𝑥, 𝑦 |𝑦 = 𝑎 𝑥2 − 𝑥1 + 𝑥2 𝑥 + 𝑥1. 𝑥2
↔ 𝑥, 𝑦 |𝑦 = 𝑎 𝑥 − 𝑥1 𝑥 − 𝑥2
*Harga Ekstrim Fungsi Kuadrat
untuk a > 0
jika 𝑥 =
−𝑏
𝑎
, maka y mencapai harga ekstrim minimum
−𝐷
4𝑎
.
jika D > 0, maka
−𝐷
4𝑎
minimum negatif.
jika D = 0, maka
−𝐷
4𝑎
minimum nol.
jika D < 0, maka
−𝐷
4𝑎
minimum positif.

11. untuk a < 0
jika 𝑥 =
−𝑏
𝑎
, maka y mencapai harga ekstrim maksimum
−𝐷
4𝑎
.
jika D > 0, maka
−𝐷
4𝑎
maksimum positif.
jika D = 0, maka
−𝐷
4𝑎
maksimum nol.
jika D < 0, maka
−𝐷
4𝑎
maksimum negatif.

12. *Grafik fungsi 𝑥, 𝑦 |𝑦 = 𝑎𝑥2
+ 𝑏𝑥 + 𝑐 terhadap sumbu x
sebagai berikut:
a. Jika a > 0 dan D > 0,
maka grafiknya:
b. Jika a > 0 dan D = 0,
maka grafiknya:
c. Jika a > 0 dan D < 0,
maka grafiknya:

13. d. Jika a < 0 dan D > 0,
maka grafiknya:
e. Jika a < 0 dan D = 0,
maka grafiknya:
f. Jika a < 0 dan D < 0,
maka grafiknya:

14. *TUGAS 2 (KELOMPOK):
Buku paket “PENGENALAN ALJABAR”
Halaman 97 – 105 no. 1-30

15. *
*PENGERTIAN SUKU BANYAK
suatu bentuk yang memuat variabel berpangkat.
suku banyak dalam x berderajat n dinyatakan
dengan:
𝑎𝑛𝑥𝑛 + 𝑎𝑛−1𝑥𝑛−1 + 𝑎𝑛−2𝑥𝑛−2 + ⋯ + 𝑎1𝑥1 + 𝑎0

16. Dengan syarat :
n ∈ bilangan cacah dan 𝑎𝑛, 𝑎𝑛−1, ..., 𝑎0 disebut koefisien-
koefisien suku banyak, 𝑎0 disebut suku tetap dan 𝑎𝑛 ≠ 0.
*NILAI SUKU BANYAK
Menentukan nilai suku banyak dapat dilakukan dua cara,
yaitu:
1. Cara Substitusi
2. Cara Horner

17. Teorema Sisa untuk Pembagian Bentuk Linear
Teorema Sisa :
TEOREMA SISA dan TEOREMA FAKTOR
1.Jika suatu suku banyak f(x) dibagi oleh
pembagi linear berbentuk (x – k), maka
sisanya adalah s = f(k).
2.Jika suatu suku banyak f(x) dibagi oleh
pembagi linear berbentuk (ax + b), maka
sisanya adalah s =  
a
b
f 
Bukti : f(x) = (x – k).H(x) + s
Jika x = k, maka f(k) = (k – k).H(k) + s
f(k) = 0.H(k) + s
f(k) = 0 + s  Sisa s = f(k) (terbukti)

18. Contoh soal :
1. Tentukan sisa pembagian suku banyak (3x4+4x3–x2+5x– 7)
oleh (x – 2)
Jawab :
S = f(2) = 3.24 + 4.23 – 22 + 5.2 – 7
= 3.16 + 4.8 – 4 + 10 – 7
= 3.16 + 4.8 – 4 + 10 – 7
= 48 + 32 – 1 = 79
Jadi sisa suku banyak di atas adalah 79
2. Suku banyak (2x3 + ax2 + bx – 2) memberikan sisa 7 jika
dibagi (2x – 3) dan habis dibagi oleh (x + 2). Tentukan nilai
a + b !
CARA SUBSTITUSI

19. Jawab :
f(x) = (2x3 + ax2 + bx – 2)
s = 7 jika dibagi (2x – 3)
 s = = 7
 
2
3
f
s = = 2 + a + b – 2 = 7
 
2
3
f  3
2
3
 
2
3
 2
2
3
  7
2
f
s 2
3b
4
9a
4
27
2
3






x 4
27 + 9a + 6b = 36
9a + 6b = 9 : 3
3a + 2b = 3 ......(1)
f(x) habis dibagi (x + 2)
 s = f(– 2) = 0
s = f(– 2) = 2(– 2)3+ a(– 2)2+ b(– 2) – 2 = 0
s = f(– 2) = – 16 + 4a – 2b – 2 = 0
2. Suku banyak (2x3 + ax2 + bx – 2) memberikan sisa 7 jika dibagi
(2x – 3) dan habis dibagi oleh (x + 2). Tentukan nilai a + b !

20. s = f(– 2) = – 16 + 4a – 2b – 2 = 0
4a – 2b = 18 : 2
2a – b = 9….......(2)
Dari persamaan (1) dan (2), kita cari nilai a dan b :
(1)….3a + 2b = 3
(2)….2a – b = 9
x 1
x 2
3a + 2b = 3
4a – 2b = 18 +
7a = 21
a = 3
Untuk menentukan nilai b, substitusikan a = 3 pada
persamaan (1) atau (2)  (2)…. 2 . 3 – b = 9  b = – 3
Jadi a + b = 3 + (– 3) = 0

21. Teorema Sisa untuk Pembagian Bentuk
Kuadrat yang dapat difaktorkan (x – a)(x – b)
Algoritma Pembagian Suku Banyak oleh (x – a)(x – b)
Jika fungsi suku banyak f(x) dibagi oleh (x–a)(x – b),
selalu dapat dituliskan :
f(x) = p(x) . H(x) + s
f(x) = (x–a)(x – b) . H(x) + s(x)
f(x) = (x–a)(x – b) . H(x) + (px+q)
P adalah koefisien x dan q adalah konstanta

22. Sehingga didapatkan :
b
a
a
f
b
b
f
a
q
dan
b
a
b
f
a
f
p






)
(
.
)
(
.
)
(
)
(
Jadi :
b
a
a
f
b
b
f
a
x
b
a
b
f
a
f
x
s






)
(
.
)
(
.
)
(
)
(
)
(
Contoh soal :
Tentukan sisa pembagian suku banyak (3x4+4x3–x2+5x– 7)
oleh x2 + x – 6 !
Jawab :
P(x) = x2 + x – 6 = (x – 2)(x + 3)
F(x) = (3x4+4x3–x2+5x– 7)
 a = 2 dan b = - 3

23. P(x) = x2 + x – 6 = (x – 2)(x + 3)
F(x) = (3x4+4x3–x2+5x– 7)
 a = 2 dan b = - 3
Jawab :
f(a) = f(2) = 3.24 + 4.23 – 22 + 5.2 – 7
= 48 + 32 – 4 + 10 – 7
= 79
f(b) = f(- 3) = 3.(- 3)4 + 4. (- 3)3 – (- 3)2 + 5. (- 3) – 7
= 243 – 108 – 9 – 15 – 7
= 104
b
a
a
f
b
b
f
a
x
b
a
b
f
a
f
x
s






)
(
.
)
(
.
)
(
)
(
)
(
Jadi :

24. )
3
(
2
79
).
3
(
104
.
2
)
3
(
2
104
79
)
(








 x
x
s
Jadi :
b
a
a
f
b
b
f
a
x
b
a
b
f
a
f
x
s






)
(
.
)
(
.
)
(
)
(
)
(
5
237
208
5
25 


 x
89
5 

 x

25. Teorema Faktor
1.Suatu fungsi suku banyak f(x) memiliki
faktor (x – k) jika dan hanya jika f(k) = 0.
2.Suatu fungsi suku banyak f(x) memiliki
faktor (ax + b) jika dan hanya jika = 0
 
a
b
f 
Contoh soal :
Buktikan bahwa (x – 2) dan (x + 3) adalah faktor-faktor dari
suku banyak (2x4 + 7x3 – 4x2 – 27x – 18) !
Bukti :
f(x) = (2x4 + 7x3 – 4x2 – 27x – 18)
• (x – 2) faktor dari (2x4 + 7x3 – 4x2 – 27x – 18)
maka f(2) = (2.24 + 7.23 – 4.22 – 27.2 – 18)

26. Bukti :
f(x) = (2x4 + 7x3 – 4x2 – 27x – 18)
• (x – 2) faktor dari (2x4 + 7x3 – 4x2 – 27x – 18)
maka f(2) = (2.24 + 7.23 – 4.22 – 27.2 – 18)
= (32 + 56 – 16 – 54 – 18) = 0
Karena f(2) = 0, maka (x – 2) adalah faktor dari f(x)
Terbukti
• (x + 3) faktor dari (2x4 + 7x3 – 4x2 – 27x – 18)
maka f(-3) = (2.(-3)4 + 7.(-3)3 – 4.(-3)2 – 27.(-3) – 18)
= (162 – 189 – 36 + 81 – 18) = 0
Karena f(-3) = 0, maka (x + 3) adalah faktor dari f(x)
Terbukti

27. Menyelesaikan Persamaan Suku Banyak
Menentukan Faktor Linear dari Suku Banyak
Jika f(x) = a0xn + a1xn-1 + … + an-1x + an dan
(x – a) merupakan faktor dari f(x), maka nilai
a yang mungkin adalah faktor-faktor bulat
dari an
Contoh soal :
Tentukan faktor-faktor dari suku banyak (2x3 – 5x2 – 14x + 8)
Jawab :
Nilai a yang mungkin adalah ±8, ±4, ±2, ±1
Dengan cara trial and error, tentukan nilai a yang mungkin
dengan mensubstitusikan ke dalan f(x) sehingga f(a) = 0
f(x) = 2x3 – 5x2 – 14x + 8

28. Untuk a = -2  f(- 2) = 0, sehingga (x + 2) merupakan faktor
dari f(x)
Untuk menentukan faktor-faktor yang lain dapat dilakukan
dengan cara HORNER sebagai berikut :
2 – 14
– 5 8
x = – 2
2
– 4 +
– 9
18
4
– 8
0  f(-2)
Sehingga :
f(x) = (x – k).H(x) + s
2x3 – 5x2 – 14x + 8 =
2x3 – 5x2 – 14x + 8 =
Jadi faktor dari 2x3 – 5x2 – 14x + 8 adalah (x + 2), (2x – 1)
dan (x – 4)
(x + 2).(2x2 – 9x + 4) + 0
(x + 2).(2x – 1)(x – 4)

29. Pembagian Suku Banyak
Hitunglah 1.256 dibagi 3 dengan cara bersusun !
Algoritma Pembagian Suku Banyak oleh (x – k)
1. Cara bersusun
Contoh soal :
Tentukan pembagian suku banyak f(x) = 3x4 + 4x3 – x2 + 5x – 7
dibagi (x – 2) !
Jawab :
3x4 + 4x3 – x2 + 5x – 7
(x – 2)
3x3
3x4 – 6x3
-
10x3 – x2 + 5x – 7
+ 10x2
10x3 – 20x2
-
19x2 + 5x – 7
+ 19x
19x2 – 38x -

30. 3x4 + 4x3 – x2 + 5x – 7
(x – 2)
3x3
3x4 – 6x3
-
10x3 – x2 + 5x – 7
+ 10x2
10x3 – 20x2
-
19x2 + 5x – 7
+ 19x
19x2 – 38x -
43x – 7
+ 43
43x – 86 -
79  sisa
 Hasil bagi
pembagi
Jadi hasil baginya = 3x3 + 10x2 + 19x + 43
dan sisanya adalah 79

31. +
2. Cara Bagan/Horner/Sintetis :
Contoh soal :
Jawab :
3 - 1
4 - 7
5
x = 2
3
6
10
20
19
38
43 79
86
 Sisa
Tentukan pembagian suku banyak f(x) = 3x4 + 4x3 – x2 + 5x –
7 dibagi (x – 2) !
Koefisien Hasil Bagi
Jadi hasil baginya = 3x3 + 10x2 + 19x + 43 dan sisanya
adalah 79

32. Pembagian Suku Banyak
Algoritma Pembagian Suku Banyak oleh (ax+b)
1. Cara bersusun
Contoh soal :
Tentukan pembagian suku banyak f(x) = 6x4 – 4x2 + 2x – 1
dibagi (2x + 4) !
Jawab :
6x4 + 0x3 – 4x2 + 2x – 1
(2x + 4)
3x3
6x4 + 12x3
-
– 12x3 – 4x2 + 2x – 1
– 6x2
– 12x3 – 24x2
-
20x2 + 2x – 1
+ 10x
20x2 + 40x -

33. 6x4 + 0x3 – 4x2 + 2x – 1
(2x + 4)
3x3
6x4 + 12x3
-
– 12x3 – 4x2 + 2x – 1
– 6x2
– 12x3 – 24x2
-
20x2 + 2x – 1
+ 10x
20x2 + 40x -
– 38x – 1
– 19
– 38x – 76 -
75  sisa
Jadi hasil baginya = 3x3 - 6x2 + 10x -19 dan
sisanya adalah 75
 Hasil bagi
pembagi
6x4 – 4x2 + 2x – 1= (2x + 4)(3x3 - 6x2 + 10x -19) + 75

34. 2. Cara Bagan/Horner/Sintetis :
Contoh soal :
Jawab :
6 – 4
0 – 1
2
x = – 2
6
– 12 +
– 12
24
20
– 40
– 38 75
76
 Sisa
Tentukan pembagian suku banyak f(x) = 6x4 – 4x2 + 2x – 1
dibagi (2x + 4) !
Jadi hasil baginya : H(x) = 3x3 – 6x2 + 10x – 19 dan
sisanya adalah f(– 2) = 75
H(x) = 



a
38
20x
12x
6x 2
3
= 3x3 – 6x2 + 10x – 19
2
38
20x
12x
6x 2
3




35. Pembagian Suku Banyak
Algoritma Pembagian Suku Banyak oleh (ax2+ bx + c)
1. Cara bersusun
Contoh soal :
Tentukan pembagian suku banyak f(x) = 4x4 – 5x2 + 3x – 1
dibagi (2x2 + x – 1) !
Jawab :
4x4 + 0x3 – 5x2 + 3x – 1
(2x2 + x – 1)
4x4 + 2x3 – 2x2
-
– 2x3 – 3x2 + 3x – 1
2x2
– 2x3 – x2 + x -
– 2x2 + 2x – 1
– x
-
– 1
– 2x2 – x + 1
3x – 2  sisa
 Hasil bagi
pembagi

36. 2. Cara Bagan/Horner/Sintetis
Contoh soal :
1. Tentukan pembagian suku banyak f(x) = 4x4 – 5x2 + 3x – 1
dibagi (2x2 + x – 1) !
*SOAL-SOAL LATIHAN
TUGAS 3 (INDIVIDU):

37. *SOAL-SOAL LATIHAN
37
.
adalah....
sisanya
)
3
(2x
dibagi
f(x)
banyak
suku
5.Jika
3)sisanya
-
(2x
dibagi
jika
dan
10
sisanya
1)
(x
dibagi
f(x)
banyak
Suku
2.
2



x

38. *SOAL-SOAL LATIHAN
38
.
adalah....
)
2
3
(x
oleh
P(x)
pembagian
sisa
1.
2)sisanya
-
(x
oleh
dibagi
jika
23)dan
-
(12x
sisanya
)
1
(x
oleh
dibagi
P(x)
banyak
suku
Suatu
3.
2
2



x

39. *SOAL-SOAL LATIHAN
39
adalah....
2
2
oleh x
P(x)
pembagian
sisa
berapa
2)
-
(x
dibagi
habis
6
4
3x
P(x)
banyak
Suku
4.
2
2
3






x
k
x
x

40. *SOAL-SOAL LATIHAN
40
.
adalah....
)
3
2
(x
oleh
h(x)
pembagian
sisa
maka
f(x).g(x)
h(x)
Jika
15.
bersisa
3)
-
(x
dibagi
jika
dan
9
-
bersisa
1)
(x
dibagi
jika
g(x)
banyak
suku
4.
bersisa
3)
-
(x
dibagi
jika
dan
8
bersisa
1)
(x
dibagi
jika
f(x)
banyak
suku
Diketahui
5.
2





x