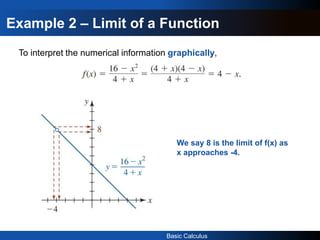
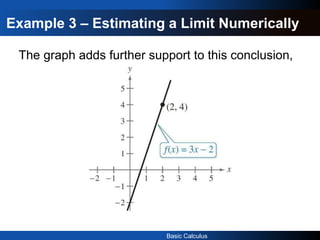
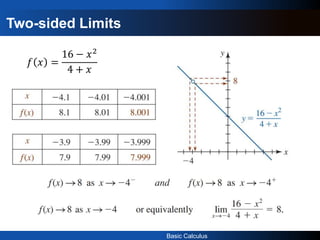
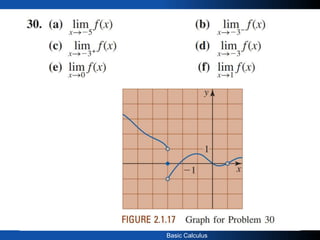
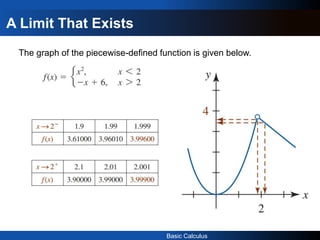
1) The document provides an introduction to the concept of limits in calculus through examples. It explains that a limit allows us to look at what happens to a function in a very small region near a point. 2) It gives examples of calculating limits numerically using tables and graphically. The limit of a function as x approaches a value a is the value that the function can be made arbitrarily close to by taking x sufficiently close to but not equal to a. 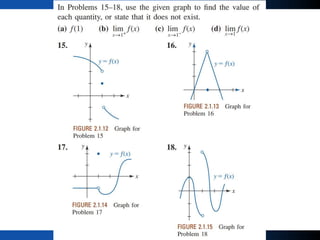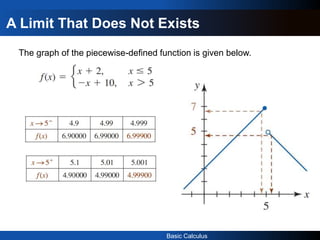3) For a limit to exist, the left-hand and right-hand limits must exist and be equal. A limit may fail to exist if the left and right-hand behavior does not agree as x approaches the value.

1. Basic Calculus
Introduction to Limits
An Informal Approach

2. Basic Calculus
Example 1 – Finding a rectangle of Maximum Area
You are given 24 inches of wire and are asked to
form a rectangle whose area is as large as
possible. What dimensions should the rectangle
have?

3. Basic Calculus
Example 1 – Solution
Let w represent the width of the rectangle, and let l
represent the length of the rectangle.
Because 2w + 2l = 24, it follows that l = 12 – w
So, the area of the rectangle is
A = lw
A = (12 – w)w
A = 12w – w2.
Using this model for area, you can
experiment with different values of w to
see how to obtain the maximum area.

4. Basic Calculus
Example 1 – Solution
After trying several values, it appears that the maximum
area occurs when w = 6 as shown in the table.
In limit terminology, you can say that “the limit of A as w
approaches 6 is 36.” This is written as
.
36
)
12
(
lim
lim 2
6
6





w
w
A
w
w

5. Basic Calculus
What is a limit?
What are some examples of limits?

6. Basic Calculus
Limits – An Informal Approach
• Up to now you have used algebra and geometry
to solve problems where things are basically
staying the same or changing at the same rate.
• Calculus is a branch of mathematics that deals
with things that are changing.
Volume of an
expanding balloon
Acceleration of rocket
ship that is changing
every part of a second
The rate of change at
any point on a curve

7. Basic Calculus
Limits – An Informal Approach
• One of the most fundamental ideas of
calculus is limits.
• Limits allow us to look at what happens in a
very, very small region around a point.
• Two of the major formal definitions of
calculus depend on limits.
What is a limit?

8. Basic Calculus
Example 2 – Limit of a Function
Consider the function,
𝑓 𝑥 =
16 − 𝑥2
4 + 𝑥
whose domain is the set of all numbers except −4.
Although 𝑓 cannot be evaluated 𝑎𝑡 − 4 because
substituting −4 for x results in the undefined
quantity 0/0
But, f(x) can be calculated at any number x that is
very close to −4

9. Basic Calculus
Example 2 – Limit of a Function
𝑓 𝑥 =
16 − 𝑥2
4 + 𝑥
As x approaches −4 from either the left or right, the function
values f(x) appear to be approaching 8.
In other words, when x is near −𝟒, f(x) is near 8.

10. Basic Calculus
Example 2 – Limit of a Function
To interpret the numerical information graphically,
We say 8 is the limit of f(x) as
x approaches -4.

11. Basic Calculus
Limit of a Function – An Informal Approach
Suppose L denotes a finite number. The notation of f(x)
approaching L as x approaches a number a can be defined
informally in the following manner.
Informal Definition
If f(x) can be made arbitrarily close to the number L by
taking x sufficiently close to but different from the
number a, from both the left and right sides of a, then the
limit of f(x) as x approaches a is L.

12. Basic Calculus
Notation
The discussion of the limit concept is facilitated by
using a special notation. If we let the arrow symbol →
represent the word approach, then the symbolism
𝑥 → 𝑎−
indicates that x approaches a number a from the left,
that is, through numbers that are less than a, and
𝑥 → 𝑎+
signifies that x approaches a from the right,
that is, through numbers that are greater than a.
𝑥 → 𝑎 signifies that x approaches a from both sides,
in other words, from the left and the right sides of a on
a number line.

13. Basic Calculus
Example 3 – Estimating a Limit Numerically
Use a table to estimate

14. Basic Calculus
Example 3 – Estimating a Limit Numerically
USING A TABLE TO ESTIMATE A LIMIT.
Solution:
Let f (x) = 3x – 2.
Construct a table that shows values of f (x) for two sets
of x-values—one set that approaches 2 from the left
and one that approaches 2 from the right.
From the table, it appears that the closer x gets to 2,
the closer f(x) gets to 4. So, you can estimate the limit
to be 4.

15. Basic Calculus
Example 3 – Estimating a Limit Numerically
The graph adds further support to this conclusion,

16. Basic Calculus
Example 4 – Estimating a Limit Graphically
Use a graph to estimate
1
1
lim
0 

 x
x
x

17. Basic Calculus
Example 4 – Estimating a Limit Numerically
Reinforce with the graph.
f(x) has a limit as x  0
even though the function
is not defined at x = 0.
.
1
1
lim
0 

 x
x
x

18. Basic Calculus
One-sided Limits
In general, if a function f(x) can be made arbitrarily close to a number L1
by taking x sufficiently close to, but not equal to, a number a from the
left, then we write
The number L1 is said to be the left-hand limit of f(x) as x approaches
a.
Similarly, if f(x) can be made arbitrarily close to a number L2 by taking x
sufficiently close to, but not equal to, a number a from the right, then L2
is the right-hand limit of f(x) as x approaches a, and we write

19. Basic Calculus
Two-sided Limits
If both the left-hand limit and the right hand limit exists and
have a common value L,
Then we say that L is the limit of f(x) as x approaches a
and write
This limit is said to be a two-sided limit.

20. Basic Calculus
Two-sided Limits
𝑓 𝑥 =
16 − 𝑥2
4 + 𝑥

21. Basic Calculus
Existence and Nonexistence
The existence of a limit of a function f as x approaches a
(from one side or both sides) does NOT depend on whether
f is defined at a but ONLY on whether f is defined for x near
the number a.

22. Basic Calculus
Existence and Nonexistence
For example, if the previous function is modified in the
following manner
Then, f(-4) is defined, and f(-4)= 5, but still, the limit is equal
to 8.

23. Basic Calculus
Existence and Nonexistence

24. Basic Calculus

25. Basic Calculus
Limits that Fails to Exist
Limits that Exist

26. Basic Calculus
Limits that Fails to Exist

27. Basic Calculus
Example 5 – Comparing Left and Right Behavior
Show that the limit does not exist by analyzing the graph.
1.)
2.)
3.)
2
0
1
lim
x
x
x
x
x 0
lim

x
x
1
sin
lim
0


28. Basic Calculus

29. Basic Calculus

30. Basic Calculus
Introduction to Limits – Extended
Still THE informal approach...

31. Basic Calculus
Based on the graph above, tell whether the limit is true or false.

32. Basic Calculus
A Limit That Exists
The graph of the function 𝑓 𝑥 = −𝑥2 + 2𝑥 + 2 is shown. As seen from
the graph and the accompanying tables, it seems plausible that
And consequently,

33. Basic Calculus
A Limit That Exists
The graph of the piecewise-defined function is given below.

34. Basic Calculus
A Limit That Does Not Exists
The graph of the piecewise-defined function is given below.

35. Basic Calculus
A Limit That Does Not Exists
The graph of the greatest integer function or floor function 𝑓(𝑥) 𝑥