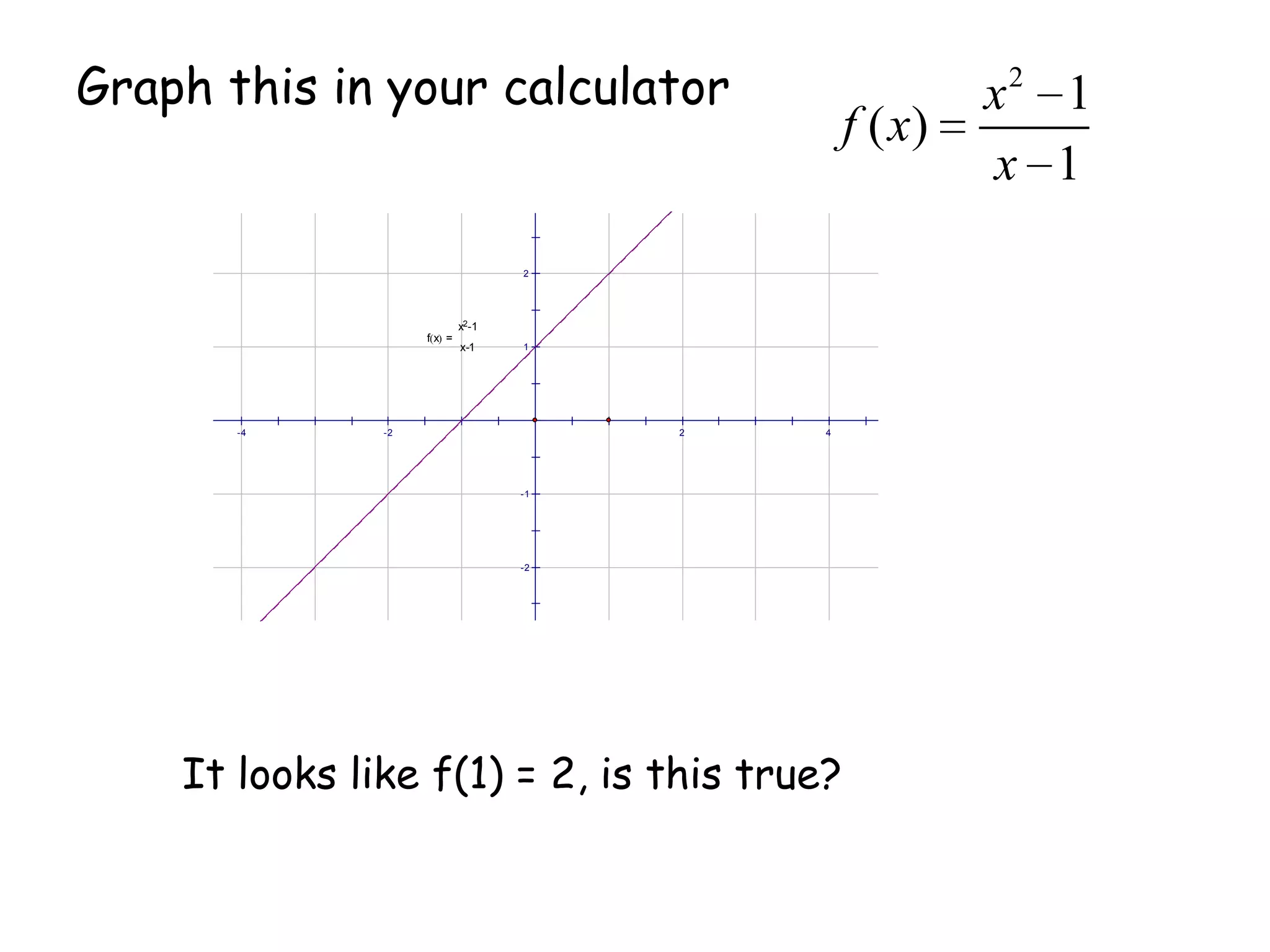
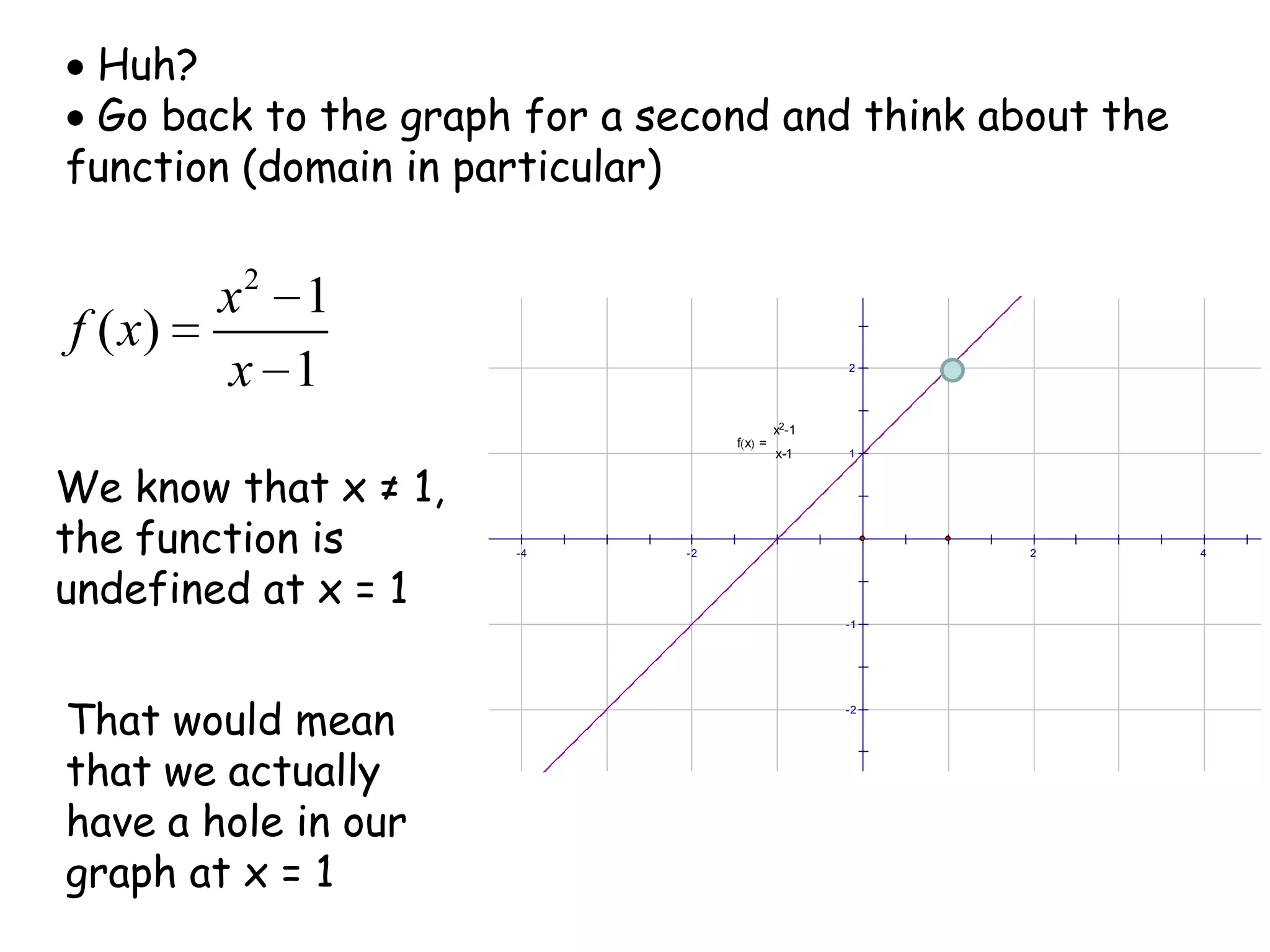
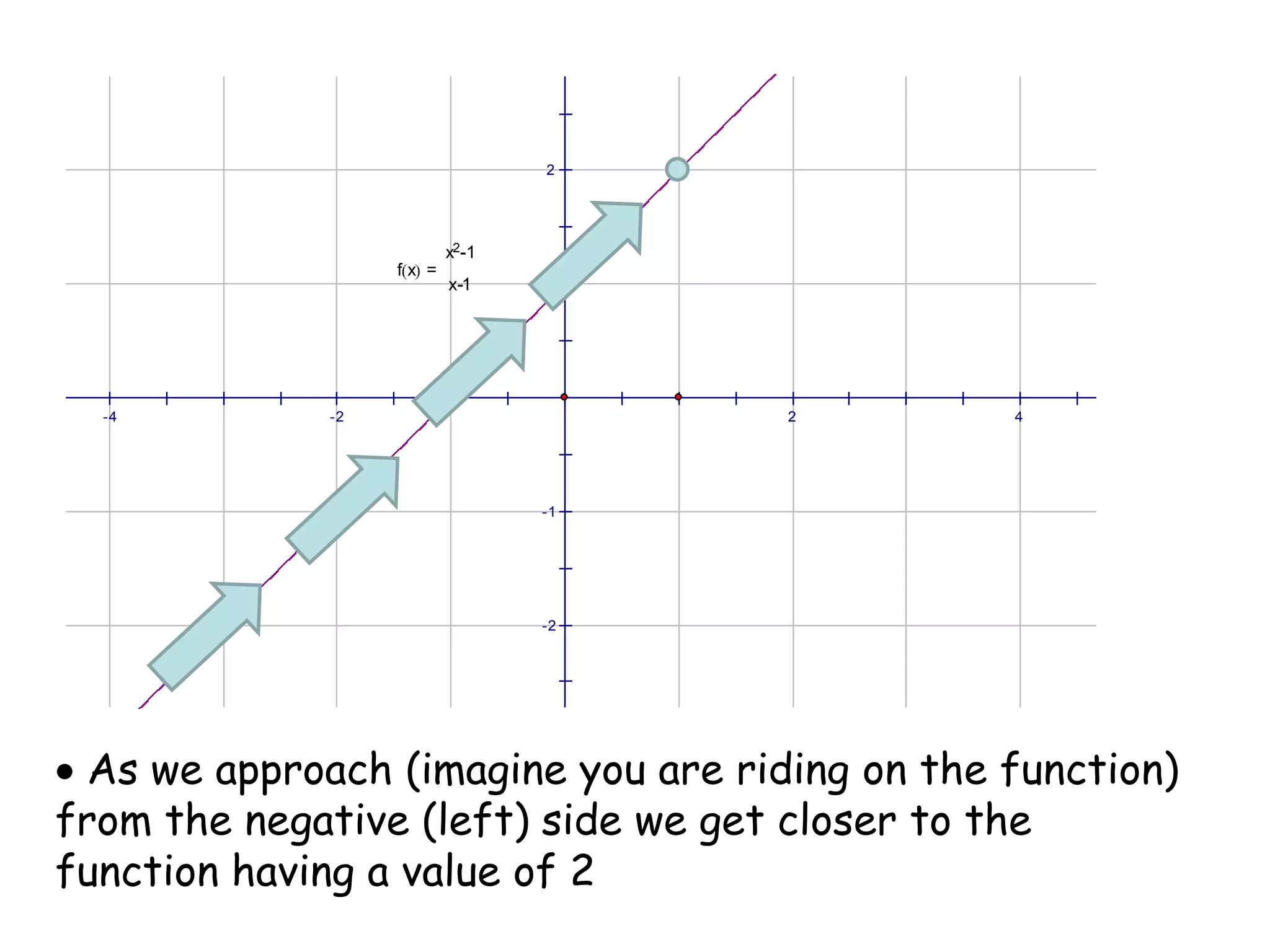
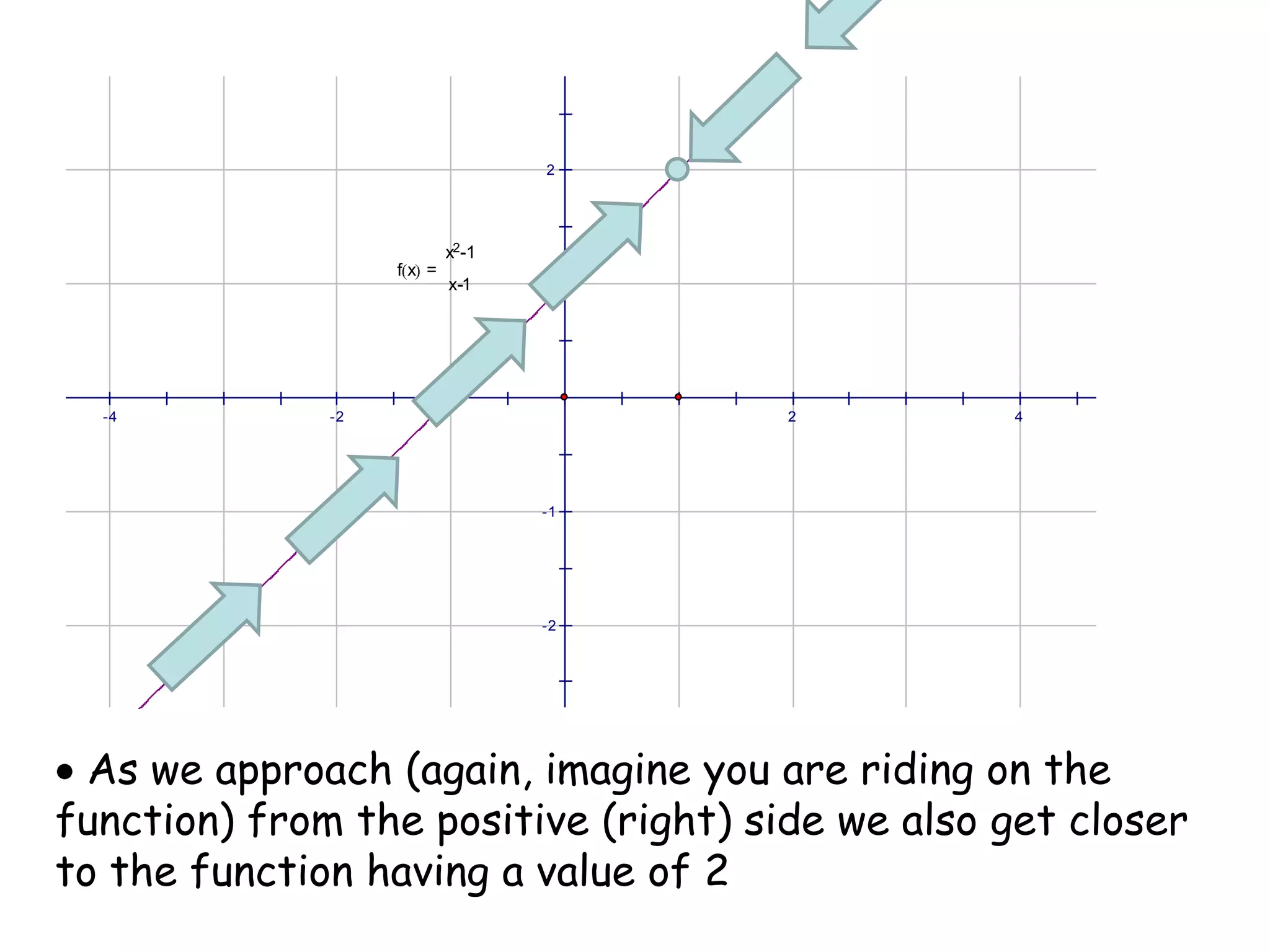
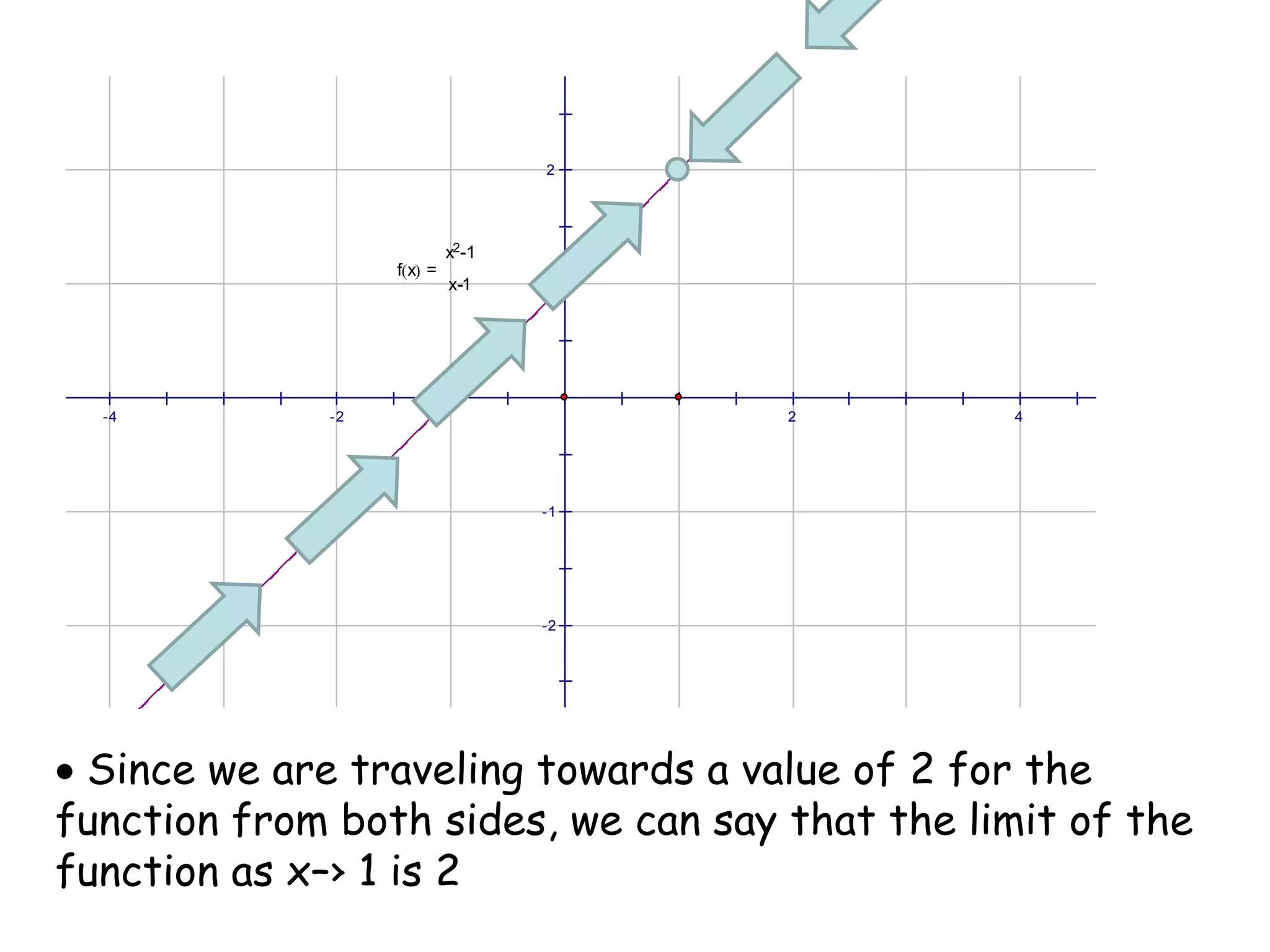
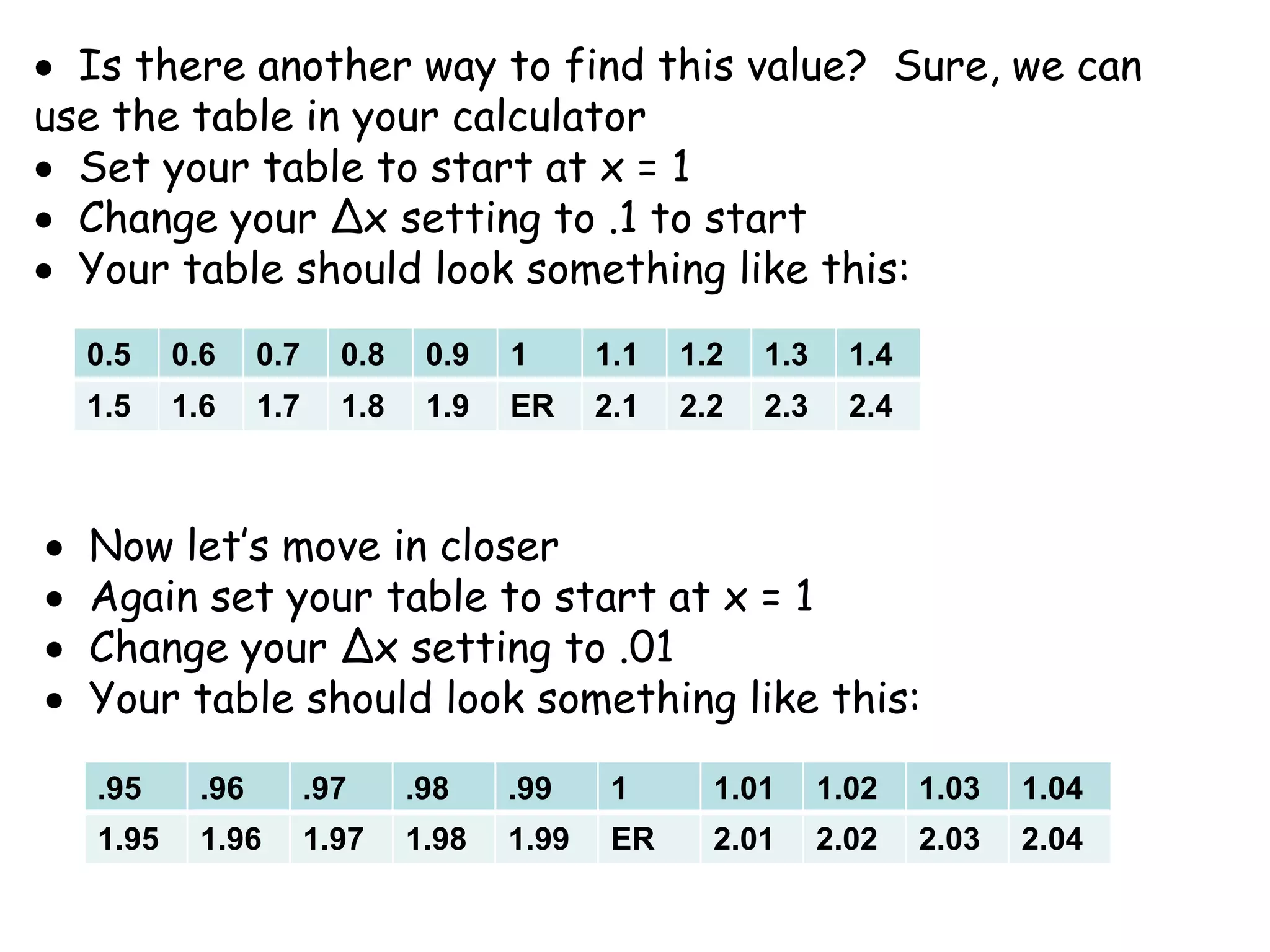
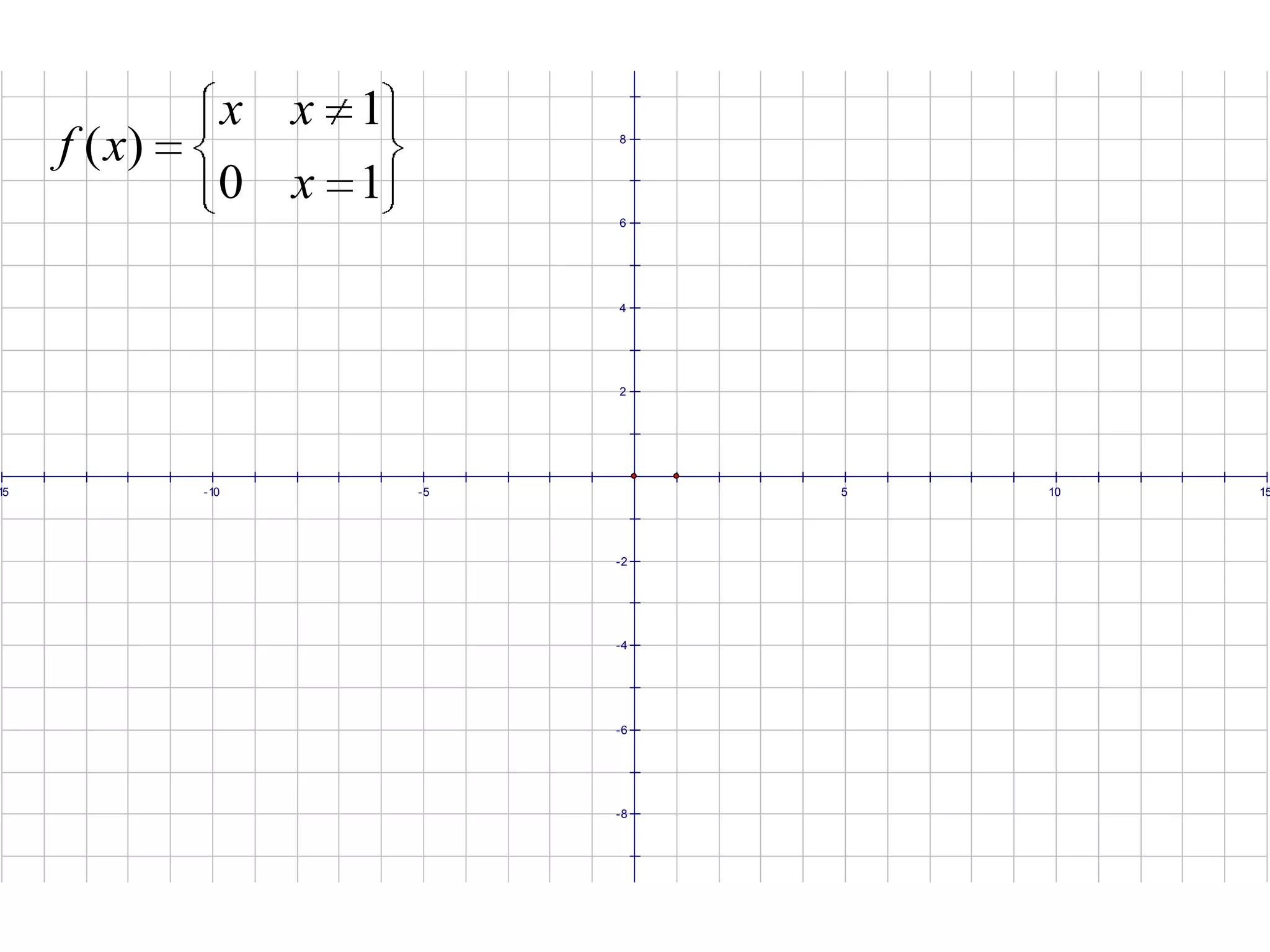
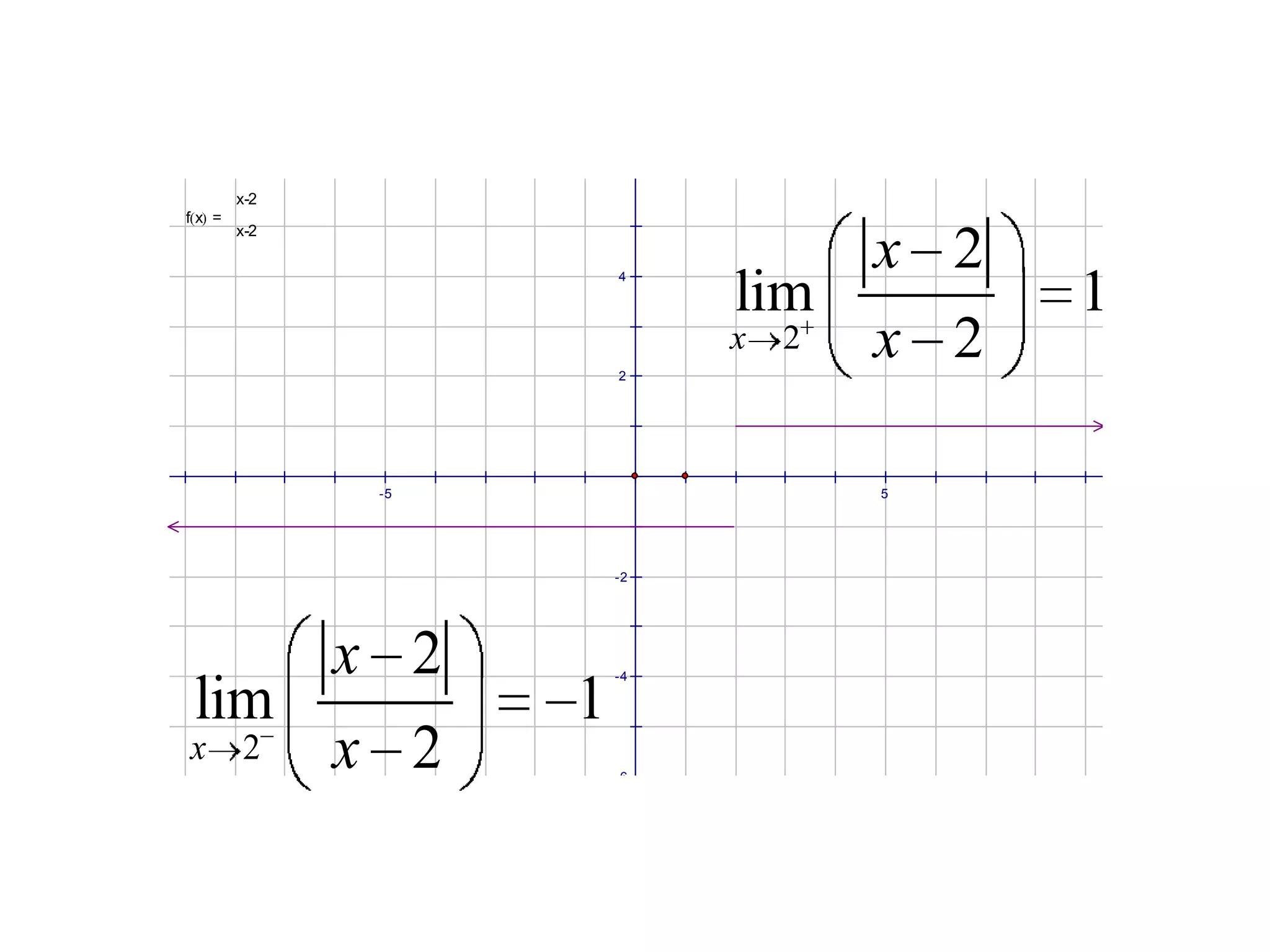
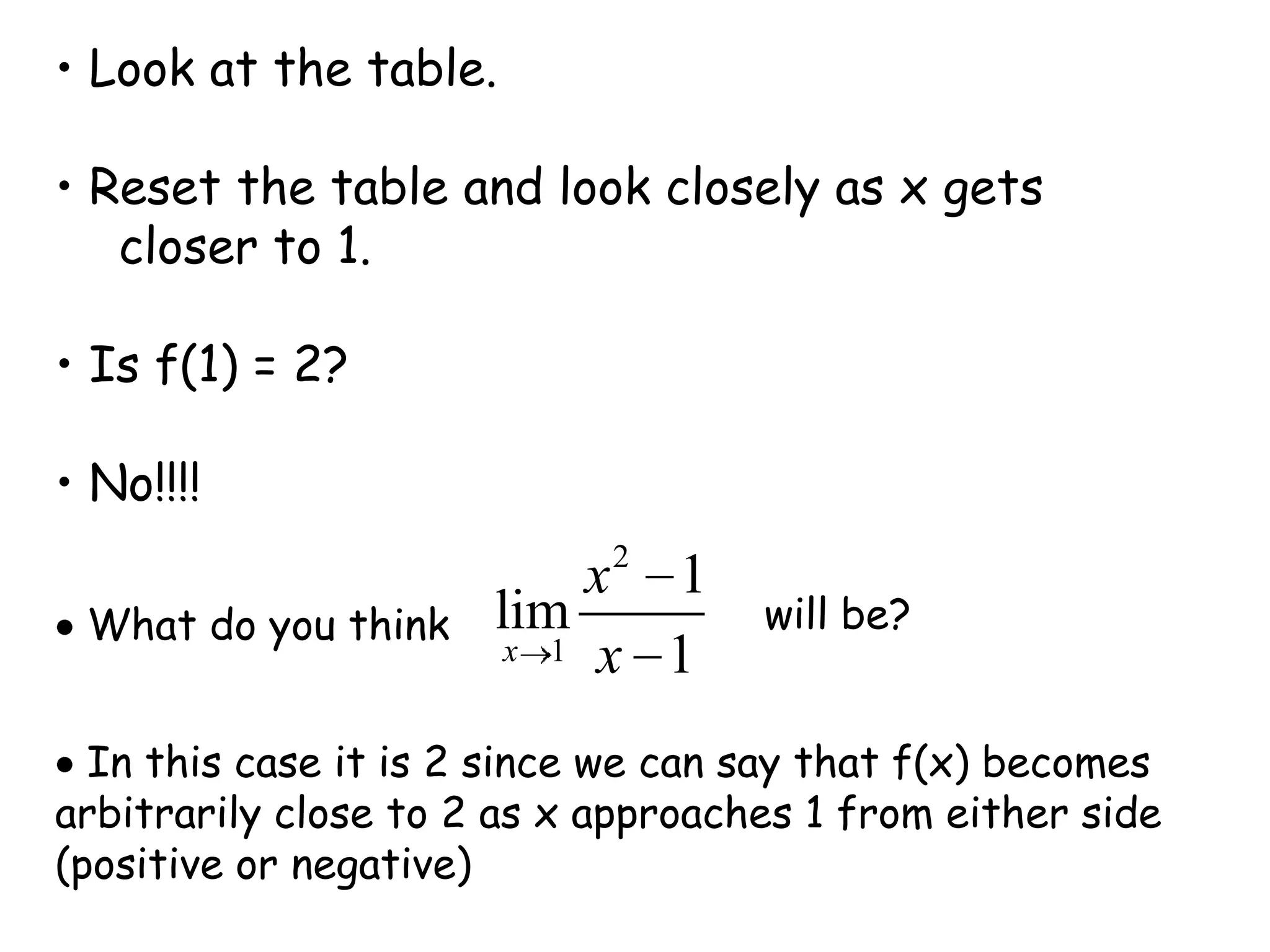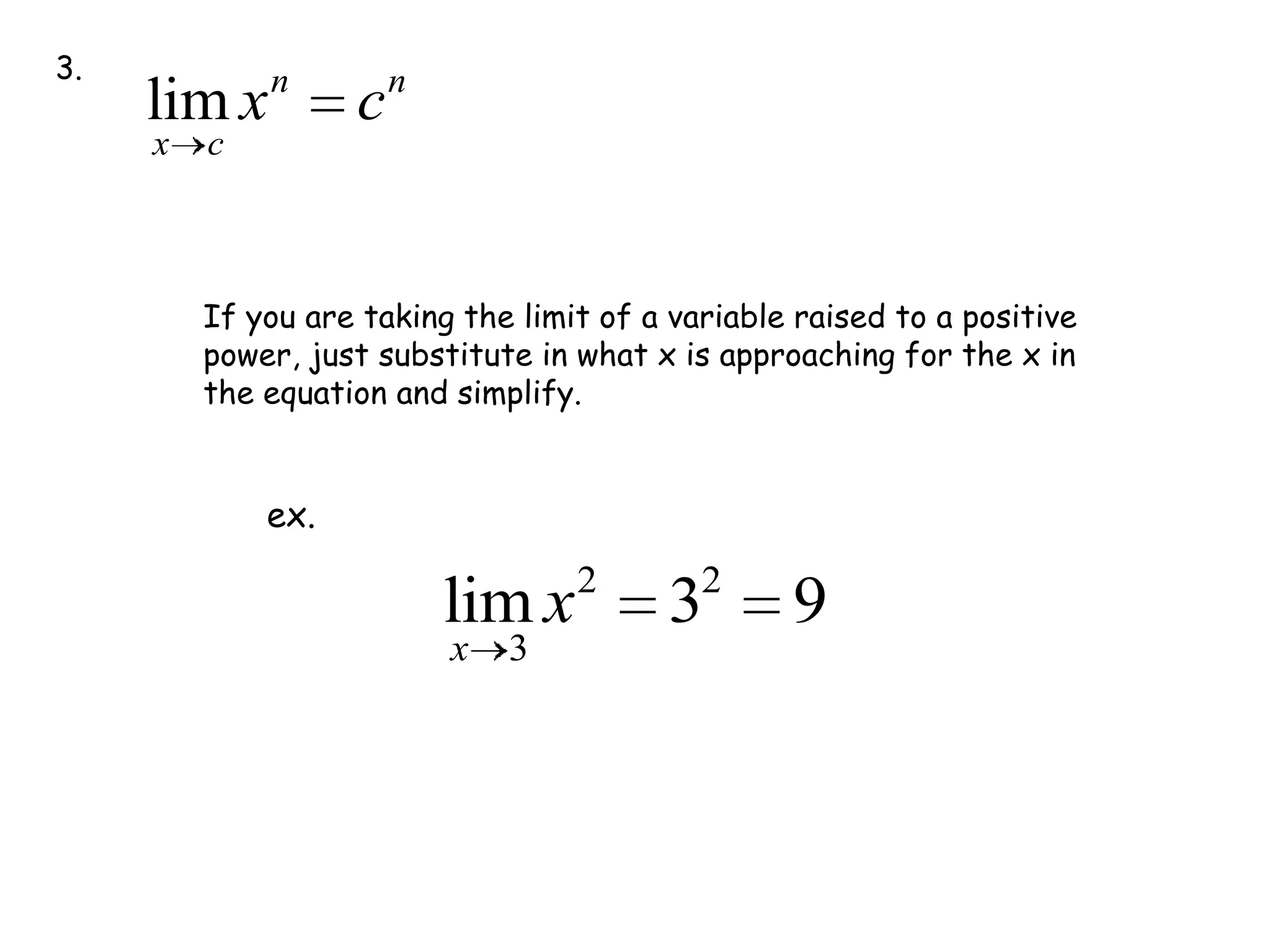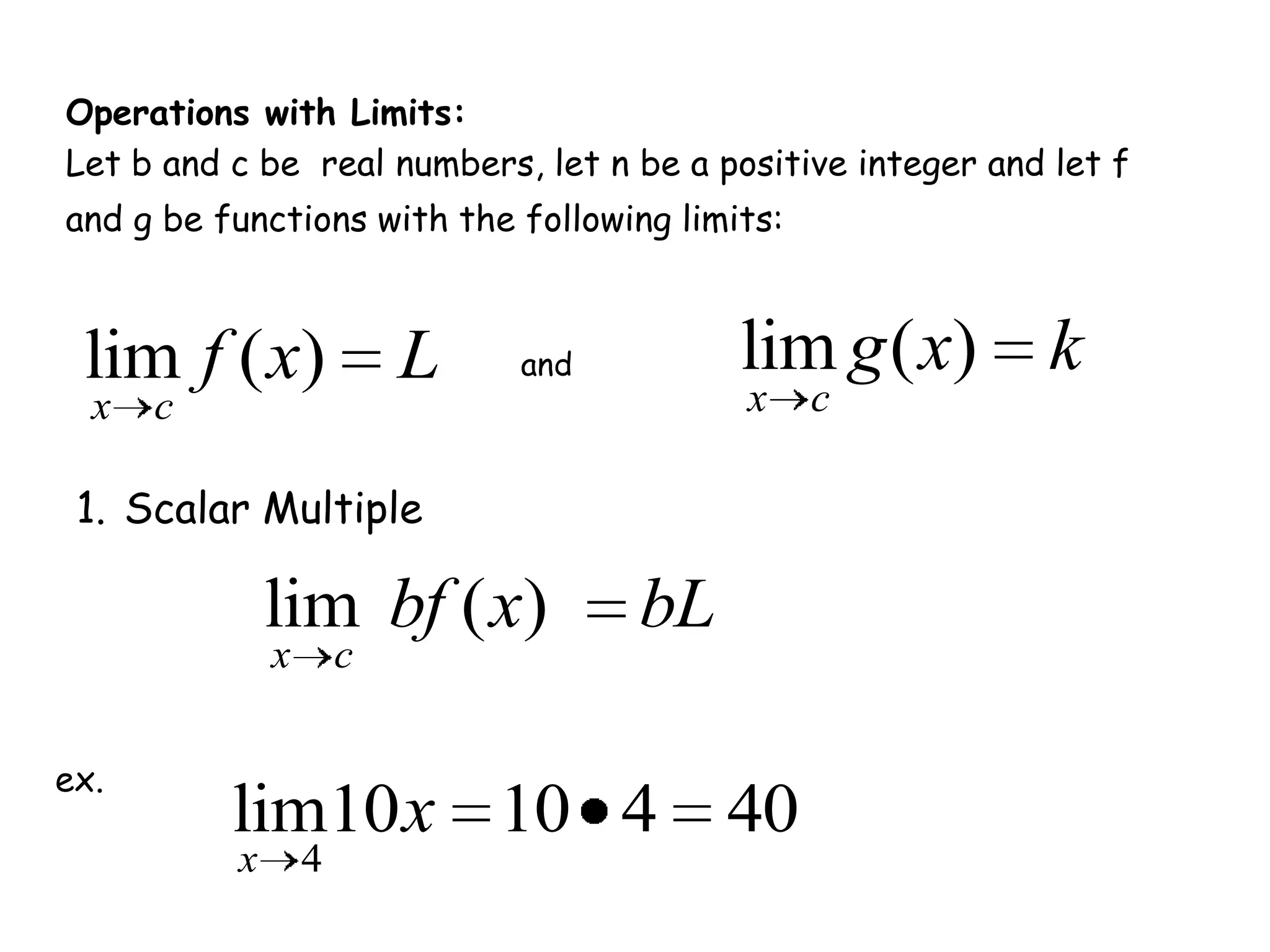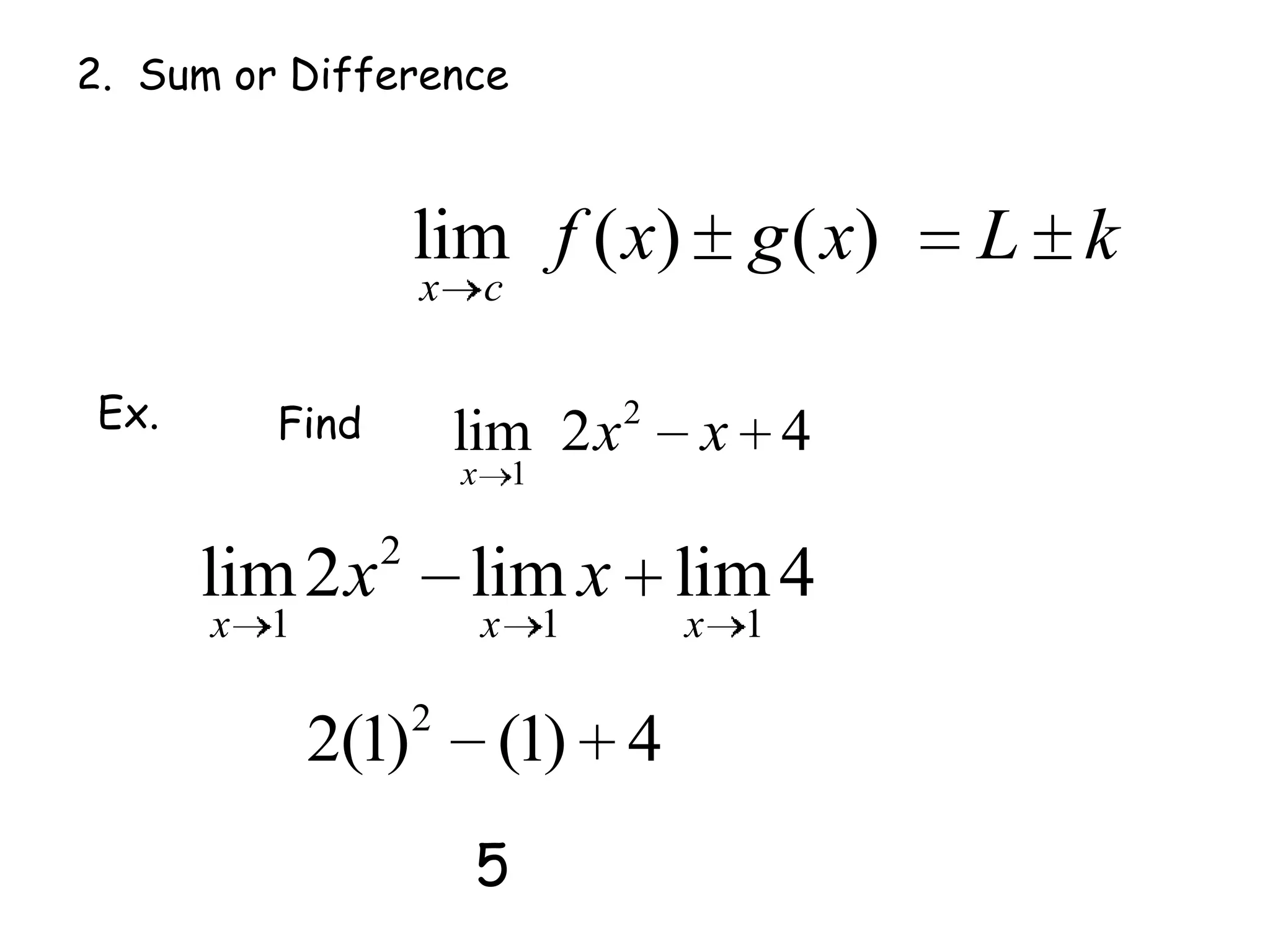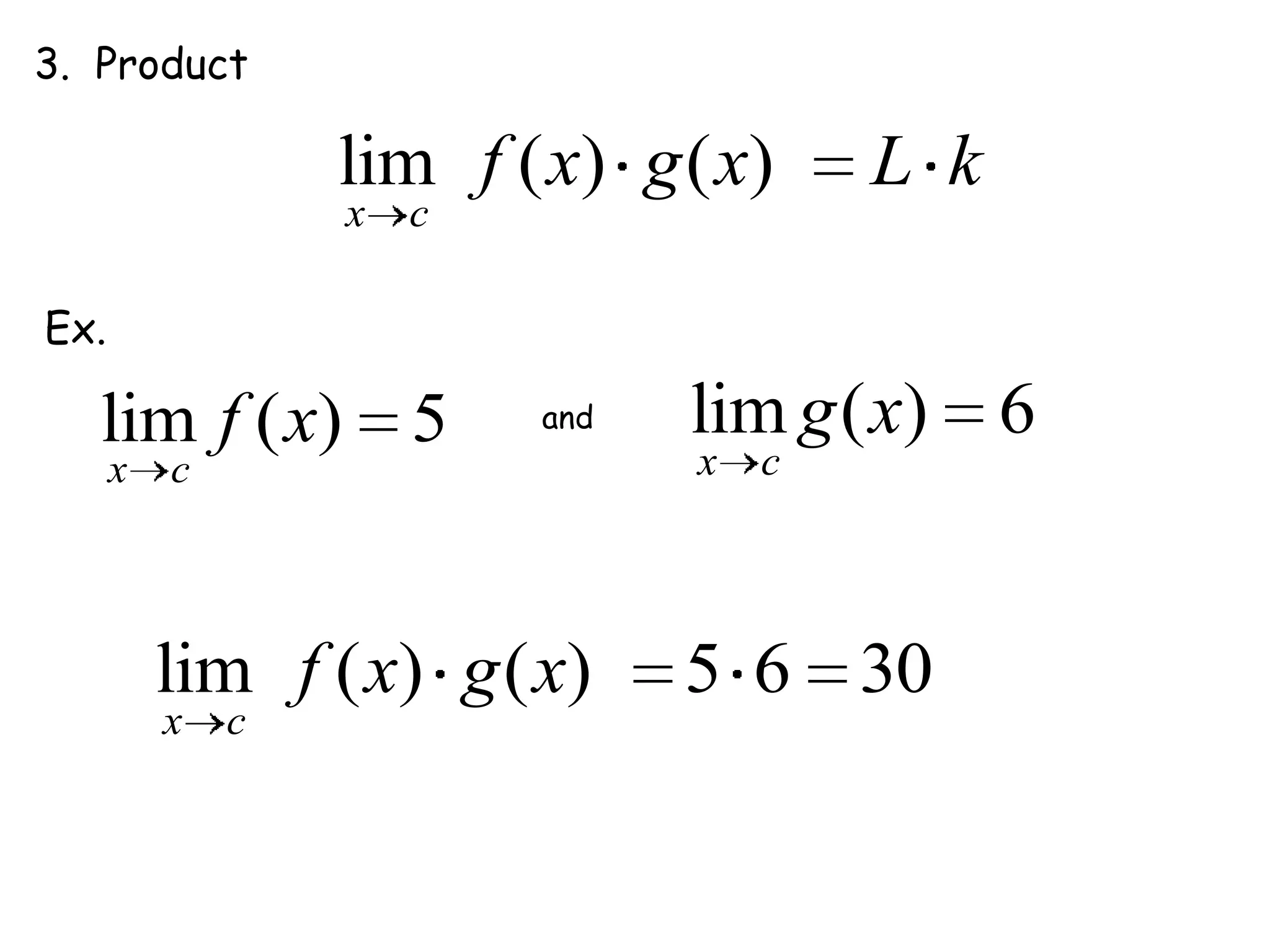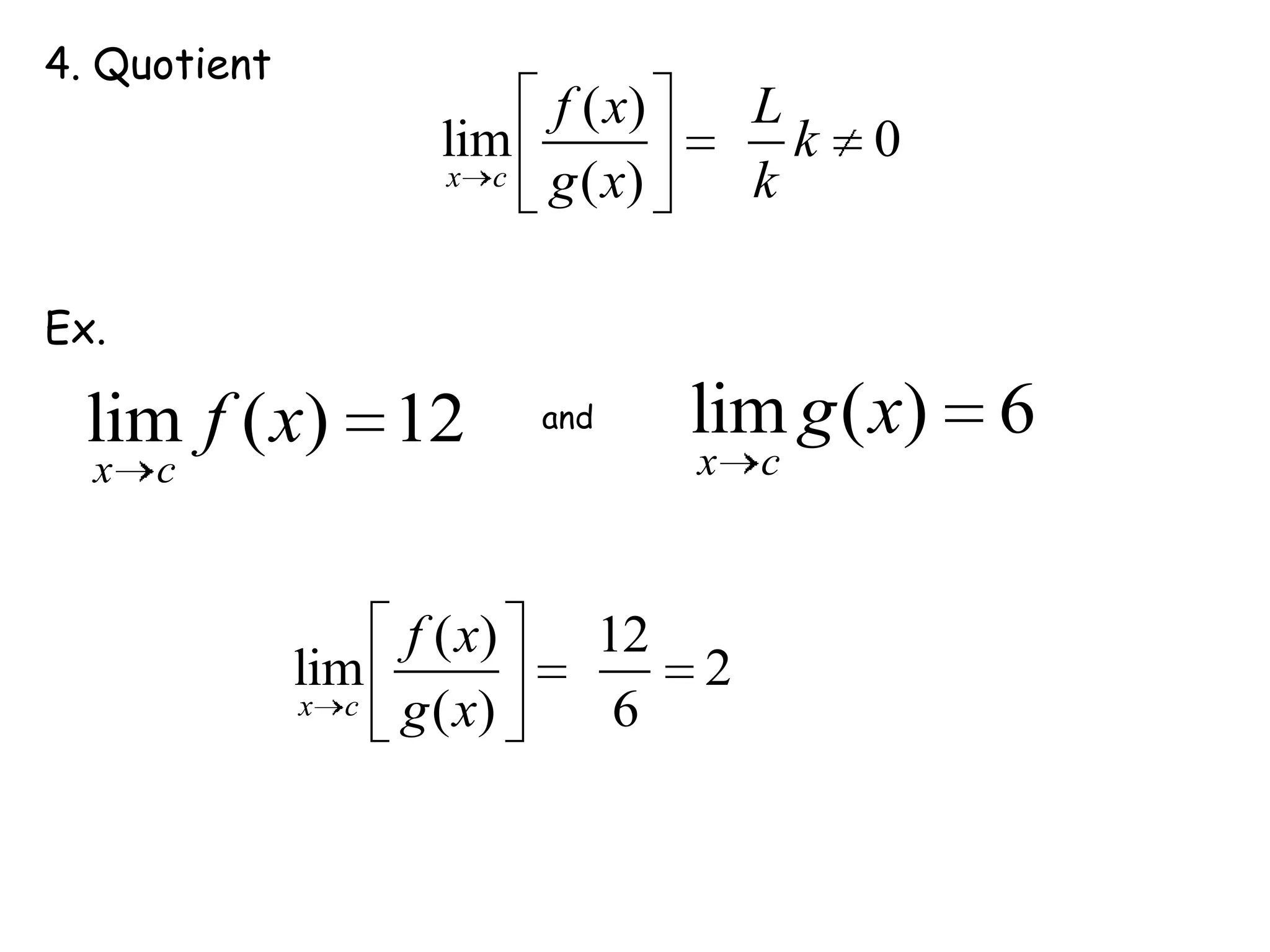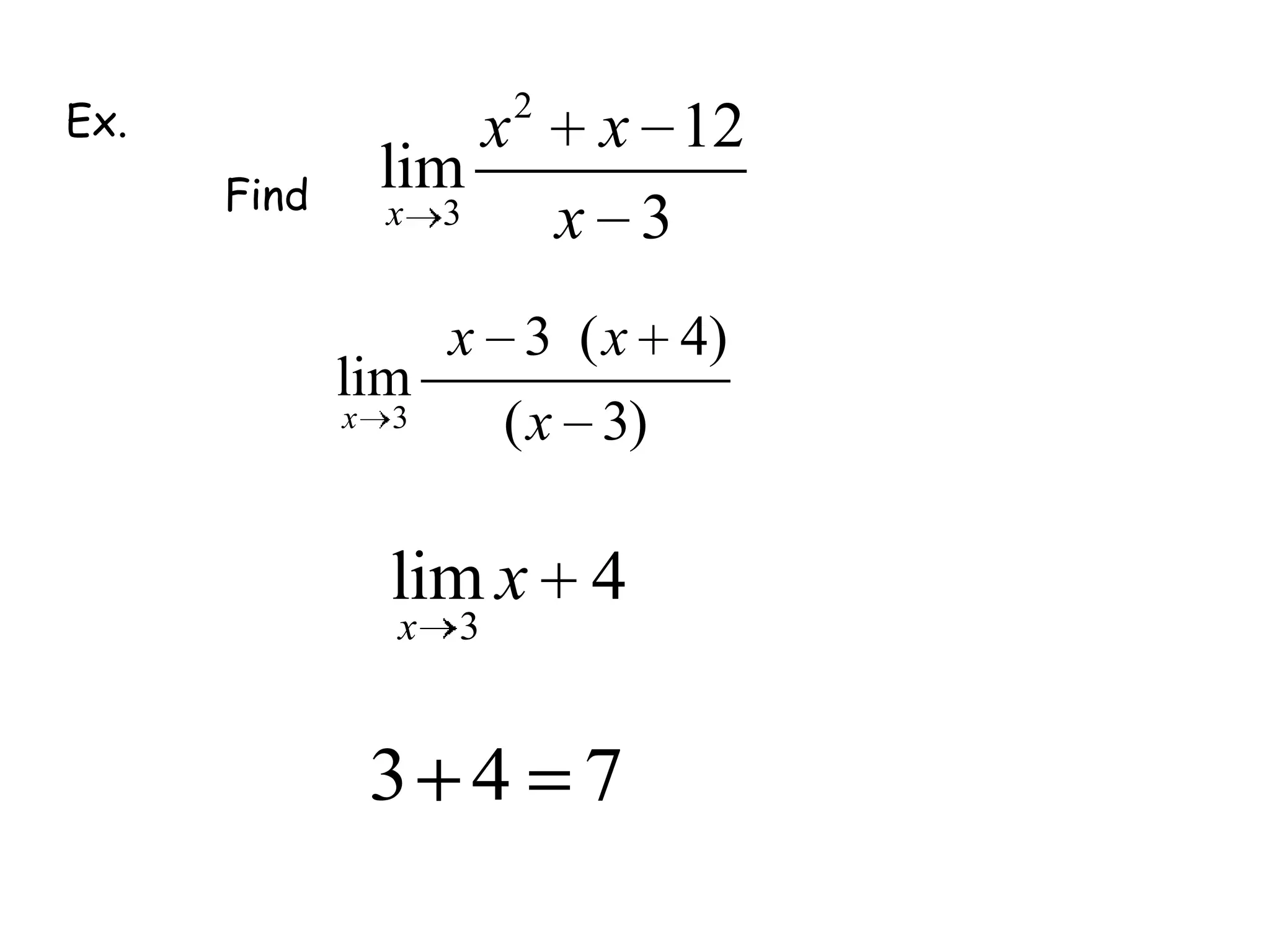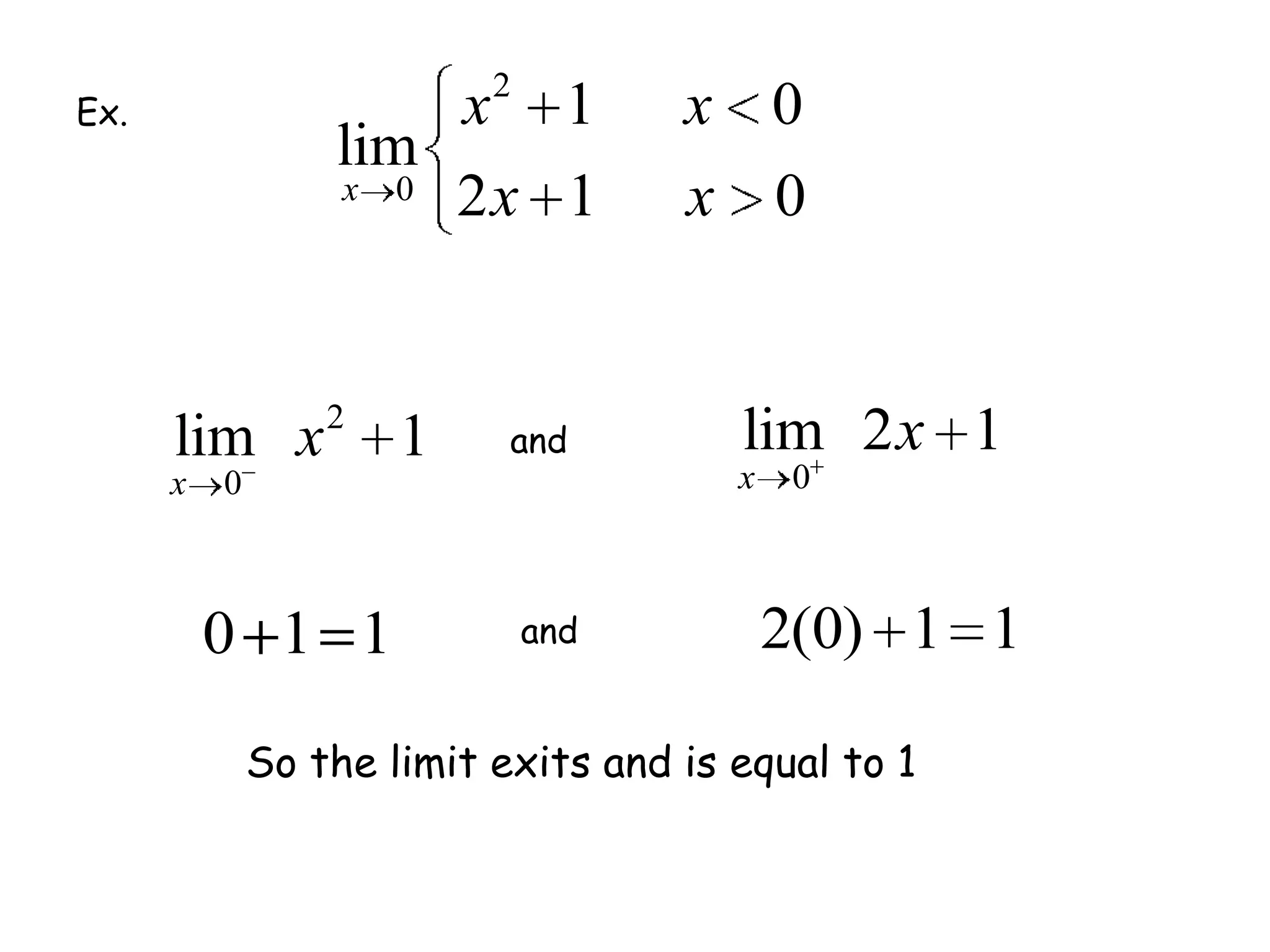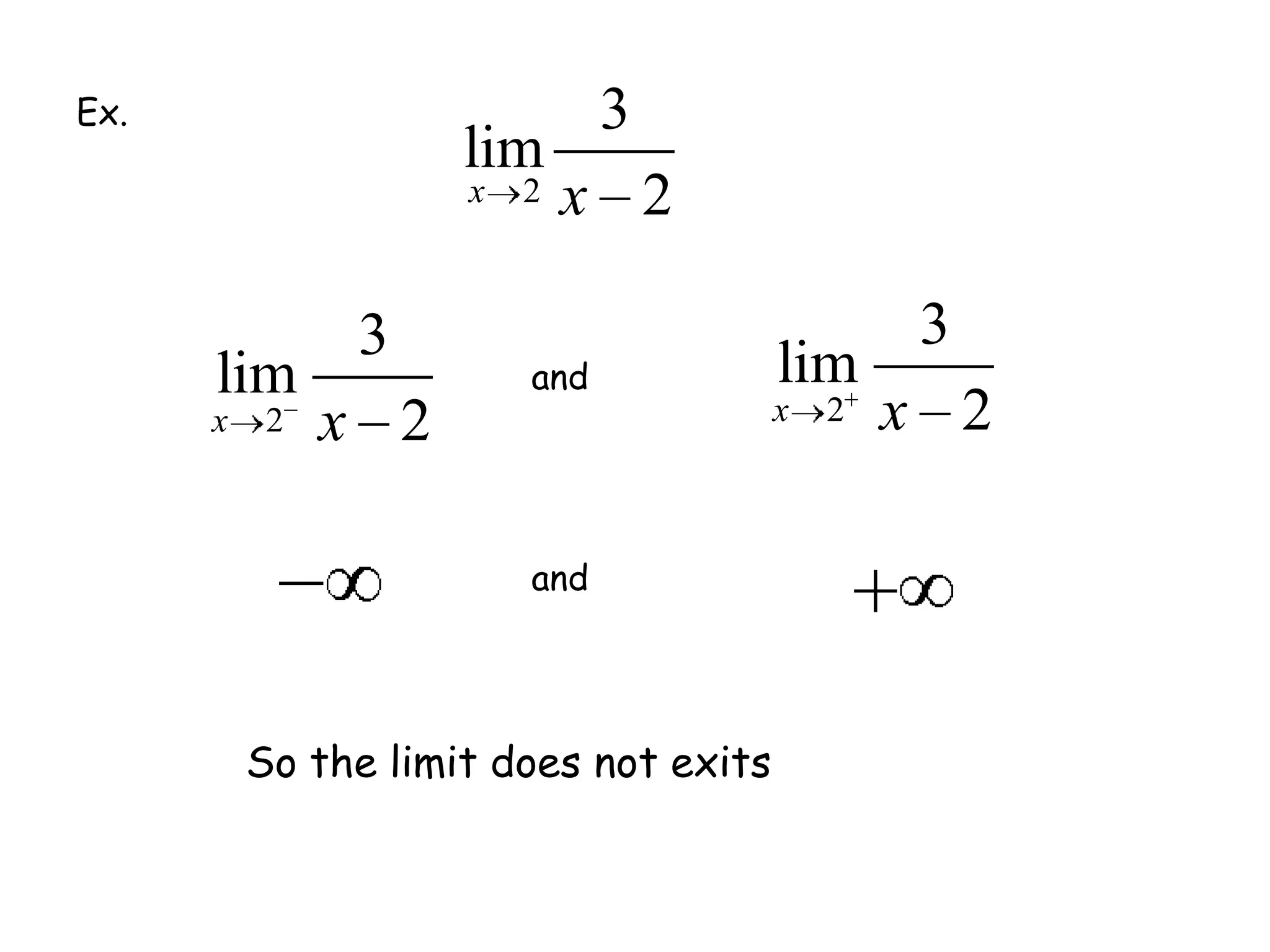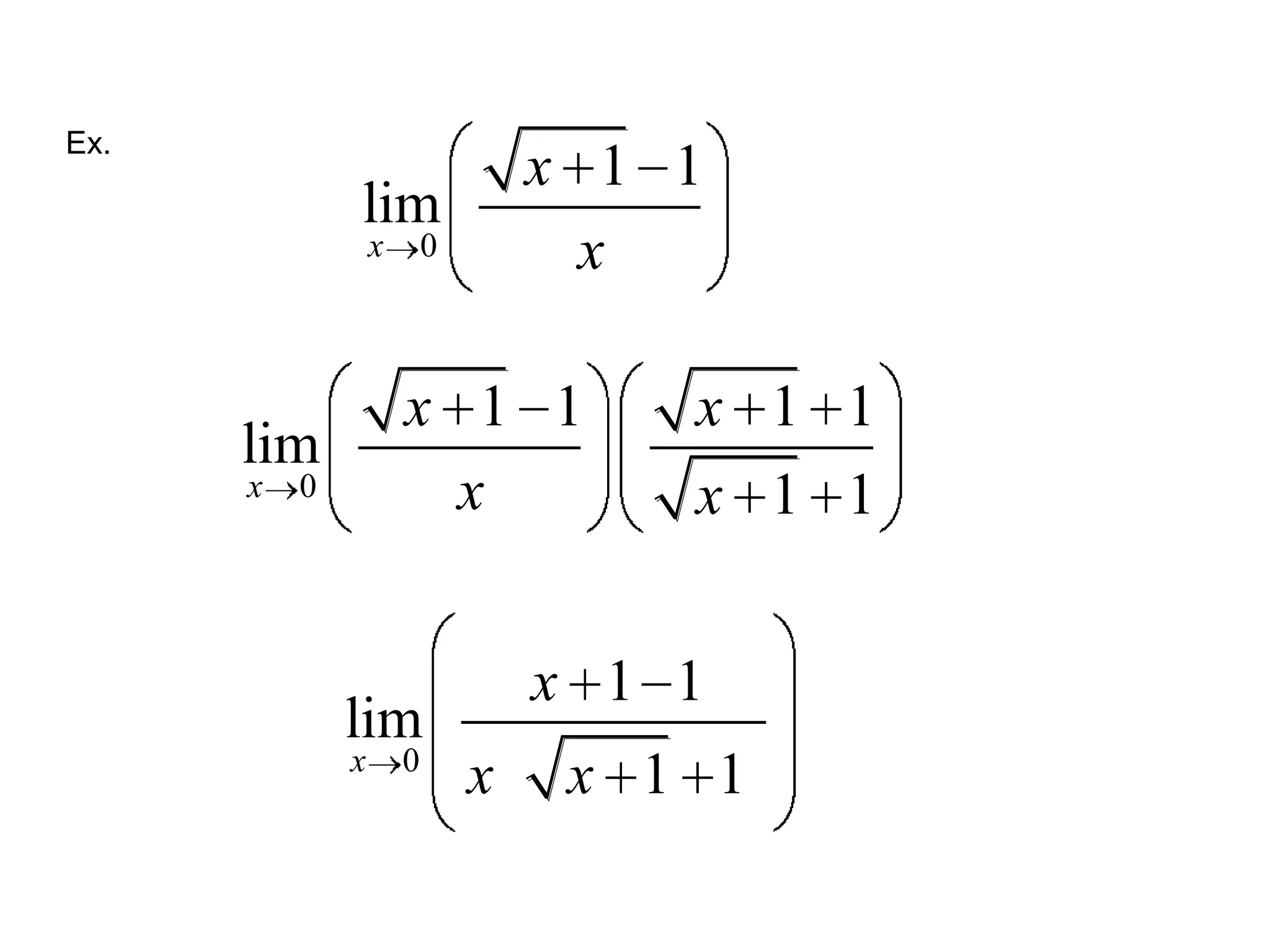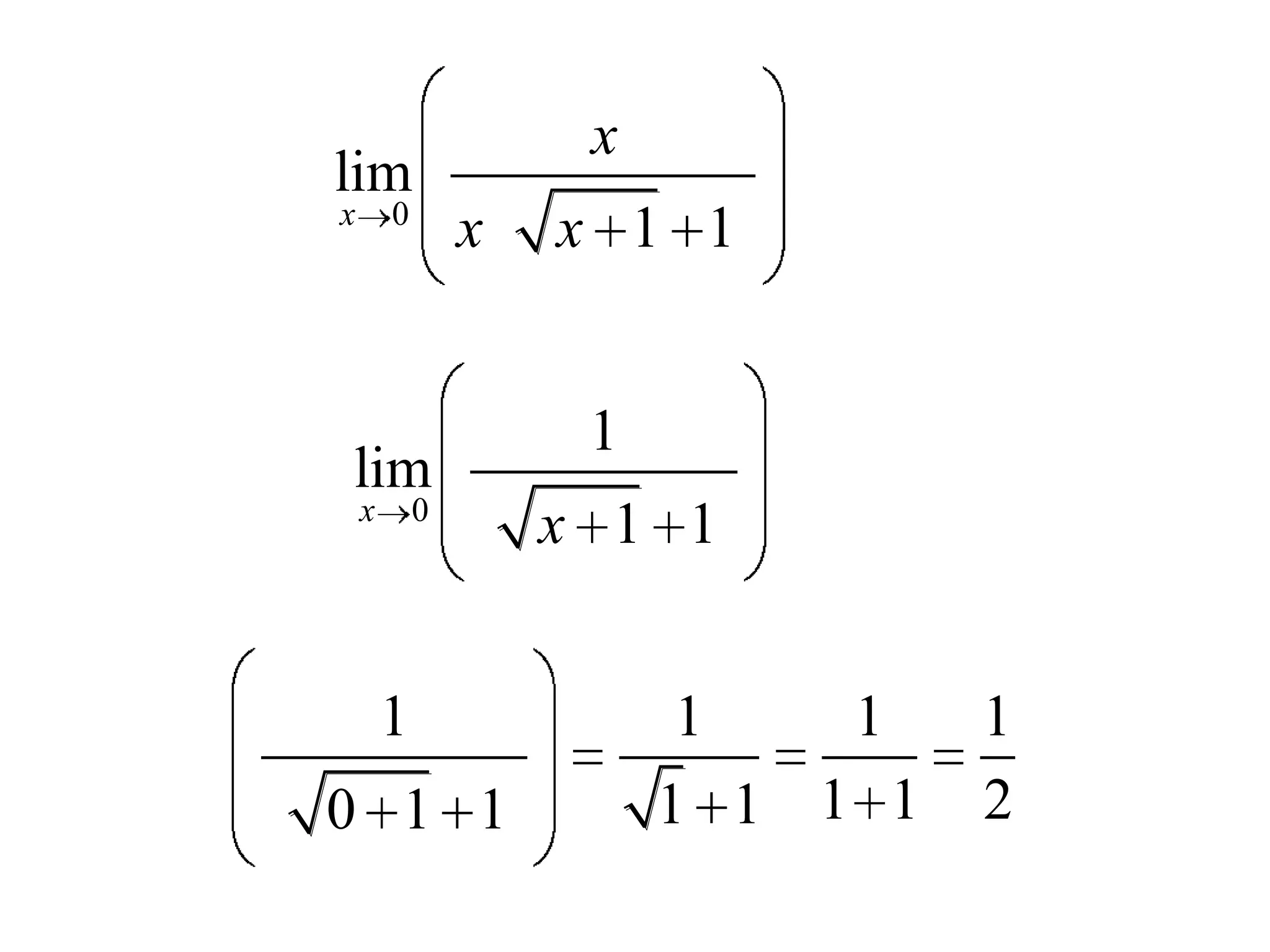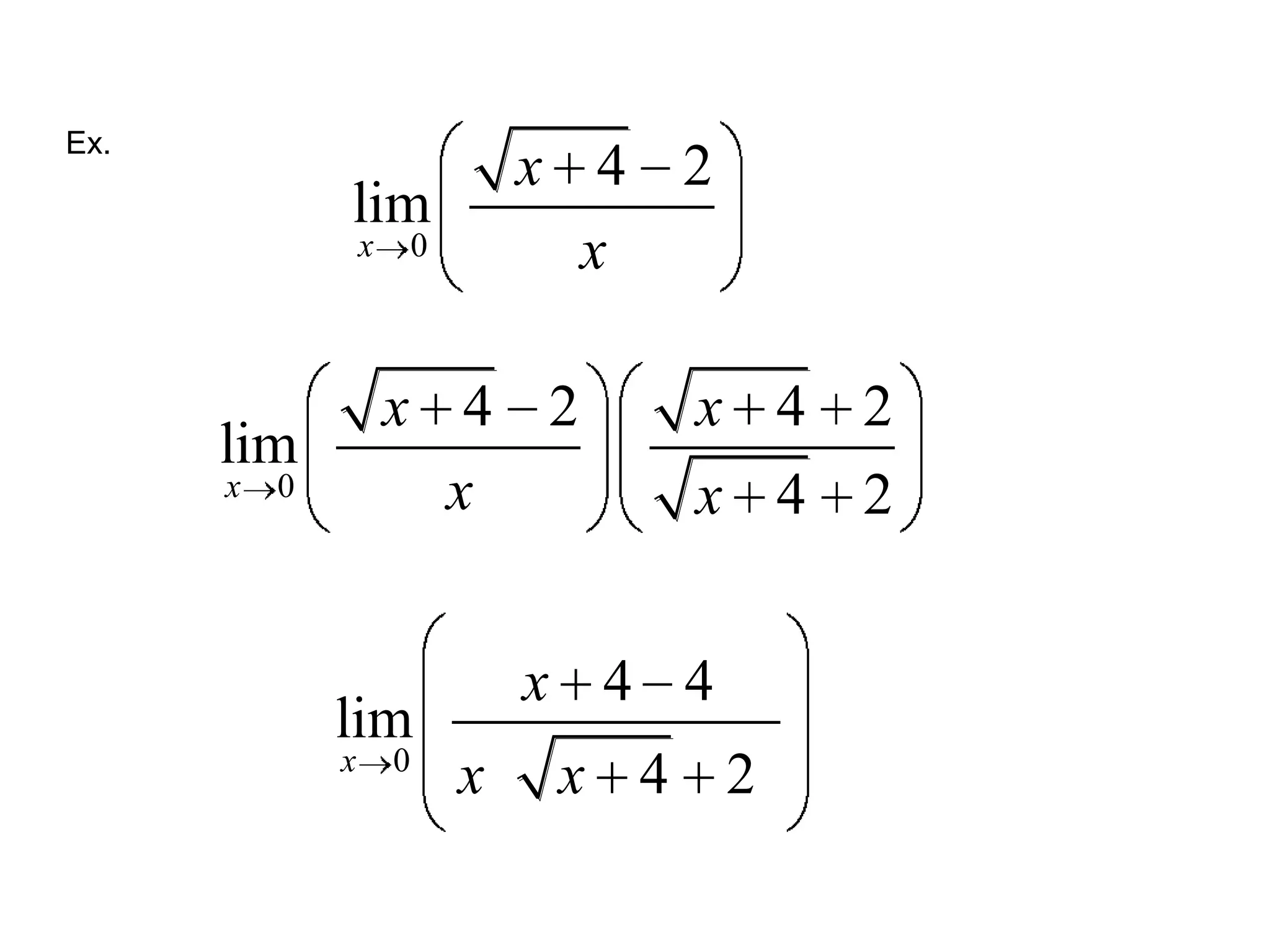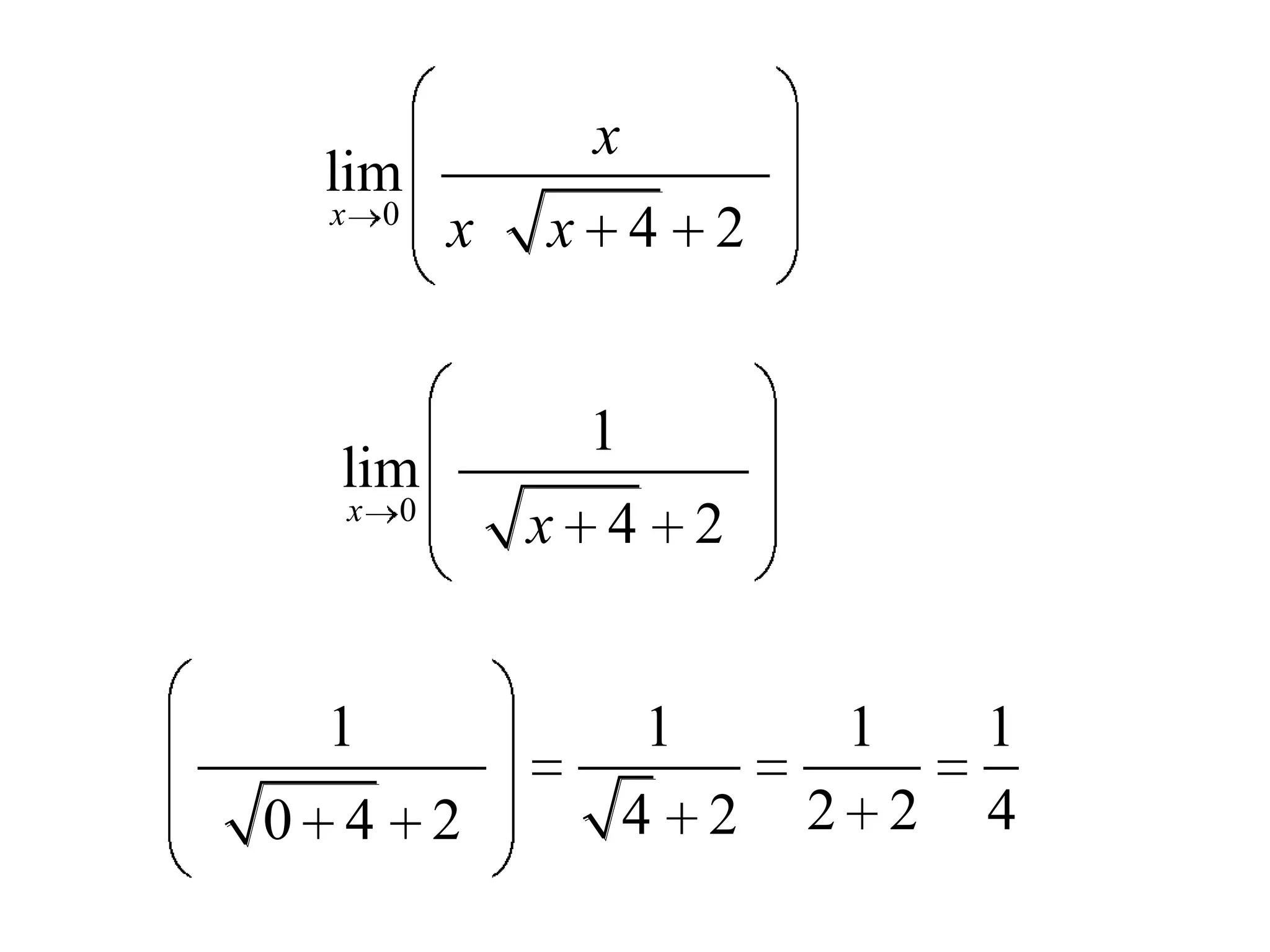This document discusses limits and how to calculate them. It defines a limit as a number a function approaches as the input value approaches a certain number. It provides examples of using graphs and tables on a calculator to find limits, and discusses direct substitution and the replacement theorem for evaluating limits. Special cases like one-sided limits, limits of polynomials, and limits involving radicals are also covered.

1. 1.5 LimitsGoal: to understand limits.def: If f(x) becomes arbitrarily close to a single number L as x approaches c from either side, then Ex.

2. Graph this in your calculatorIt looks like f(1) = 2, is this true?

3. Look at the table.

4. Reset the table and look closely as x gets closer to 1.

5. Is f(1) = 2?

6. No!!!!will be? What do you think

7. In this case it is 2 since we can say that f(x) becomes arbitrarily close to 2 as x approaches 1 from either side (positive or negative) Huh?

8. Go back to the graph for a second and think about the function (domain in particular)We know that x ≠ 1, the function is undefined at x = 1That would mean that we actually have a hole in our graph at x = 1

9. As we approach (imagine you are riding on the function) from the negative (left) side we get closer to the function having a value of 2 As we approach (again, imagine you are riding on the function) from the positive (right) side we also get closer to the function having a value of 2 Since we are traveling towards a value of 2 for the function from both sides, we can say that the limit of the function as x–› 1 is 2 Is there another way to find this value? Sure, we can use the table in your calculator

10. Set your table to start at x = 1

11. Change your ∆x setting to .1 to start

12. Your table should look something like this:

13. Now let’s move in closer

14. Again set your table to start at x = 1

15. Change your ∆x setting to .01

16. Your table should look something like this: One last time even closer

17. Again set your table to start at x = 1

18. Change your ∆x setting to .001

19. Your table should look something like this:

20. We can probably guess pretty accurately that the limit is equal to 2Limit rules:A limit only exists if both the left side and the right side approach the same value!!!! THIS is VERY IMPORTANT!!!!!Ex.does exist?Graph in your calculator. Look at the table as x gets closer to 1

21. What value is the function approaching from the left side?

22. -1

23. What is value is the function approaching from the right side?

24. 1Since the left side limit ≠ right side limit, we say that the limit does not exist.find Ex.Graph the function first, remember how to graph a piecewise function.

26. Ex.Find How can I figure this one out?

27. Graph?

28. Yes

29. Table?

30. Yes

31. What do you think the limit is?

32. 7

33. What if I forgot my calculator today? Or my batteries died? How did people do limits before there were calculators?Direct Substitution:When the domain does not create difficulty for us (undefined, etc.), we can substitute what x approaches directly into the function.

34. Go back to our first example. You must have figured by now that there was a reason we went back and reviewed all of our algebra skills. Simplify first!Now Direct Substitution works, we can substitute x = 1 into the function to find the value the function is approaching.Remember this is not necessarily solving for the actual value of the function, it is looking for what value the function is approaching as x -> that specific number. Often x is approaching a number that will make the function undefined!

35. Properties and Operations with Limits:Let b & c be real numbers and let n be a positive integer.If you are taking the limit of a constant the limit is just that constant.ex.

36. 2.If you are taking the limit of a lone variable just substitute in what x is approaching for the x in the equation.ex.

37. 3.If you are taking the limit of a variable raised to a positive power, just substitute in what x is approaching for the x in the equation and simplify.ex.

38. 4. If you are taking the limit of a variable under a radical, just substitute in what x is approaching for the x in the equation and simplify. Be careful that when your index is even then c must be positive!ex.

39. Operations with Limits:Let b and c be real numbers, let n be a positive integer and let f and g be functions with the following limits:andScalar Multipleex.

40. 2. Sum or DifferenceEx.Find 5

41. 3. ProductEx.and

42. 4. QuotientEx.and

43. The Limit of a Polynomial:If p is a polynomial function and c is any real number thenCan you think of a method that allows us to substitute values into polynomials very easily?Synthetic Substitution!

44. Ex.Find

45. The Replacement Theorem:Let a be a real number and let f(x)=g(x) for all x≠c. If the limit of g(x) exists as x->c then the limit of f(x) also exists andThis is just the theorem that actually allows us to simplify before we take limits.

46. Ex.Direct substitution won’t work here. We would be dividing by zero.Find Here is a place where it is very helpful to remember how to factor the difference of cube. Again, that is why we reviewed it:-)

47. Ex.Find

48. One Sided Limits: When the limit doesn’t exist (since the left and right side are approaching at very different values) we look at one sided limits.Graph:

49. Does the limit as x->2 exist?Left side (see the little negative sign)Right side (see the little positive sign)

51. Existence of a Limit: If f is a function and c and L are real numbers theni.f.f. both the left and right hand limits are equal to L.So:For the limit to exist

52. Ex.andandSo the limit exits and is equal to 1

53. Unbounded Behavior: When the function approaches +∞ or -∞ as x->c, we say the function is unbounded. The limit does not exist.Graph:

55. Ex.andandSo the limit does not exits

56. Unbounded Behavior: When the function approaches +∞ or -∞….Think about that statement for a minute.Remember,+∞ and -∞ are not numbers, when we say something is approaching +∞ or -∞, we are not giving an exact numerical answer.That is why the function is unbounded and the limit does not exist

57. Special Cases with RadicalsWhat about functions where direct substitution doesn’t work?If you can’t divide out factors, try to rationalize the numerator to get a larger expression in the denominator.To rationalize the numerator, you use the same strategies that you use to rationalize the denominator, but this time you are actually trying to put the radical into the denominator!

58. Ex.

60. Ex.

62. Homework Problems: 2.3. 4.