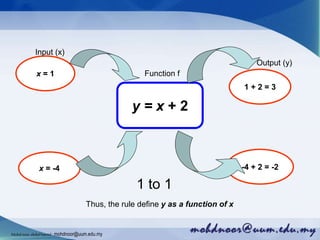
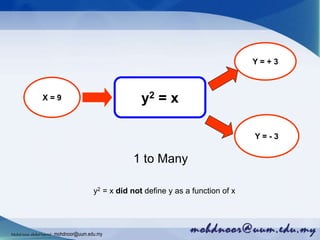
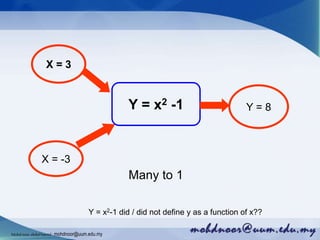
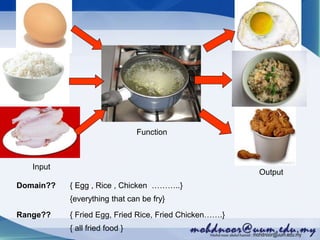
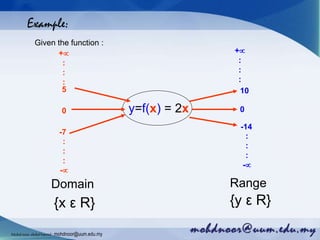
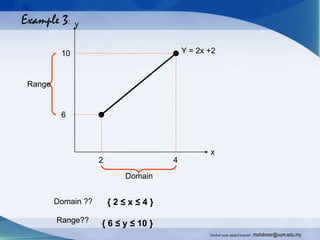
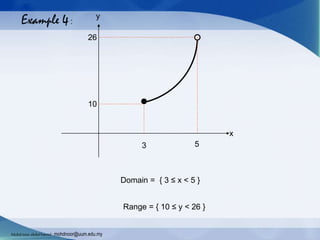
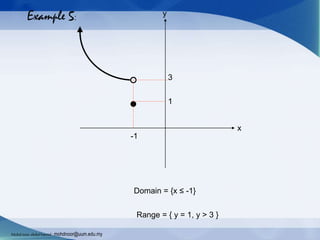
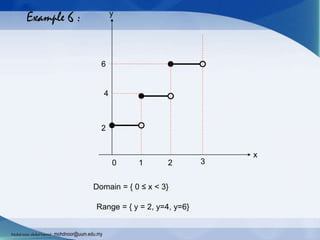
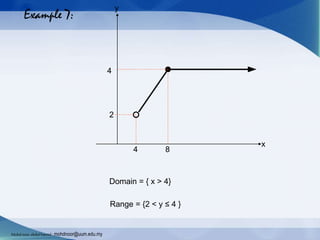
The document provides an introduction to functions and their notation, detailing concepts such as input/output relationships, domain, and range. It covers examples of calculating function values and determining whether a given relationship is a function. Additionally, it highlights different types of functions and outlines how to define their domains and ranges.