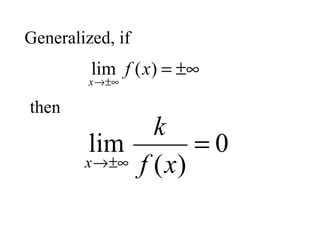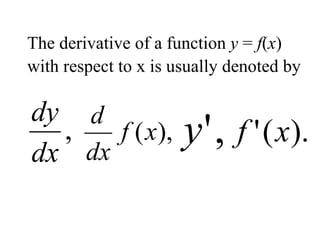The document discusses functions and their derivatives. It defines functions, different types of functions, and notation used for functions. It then covers the concept of limits, theorems on limits, and limits at infinity. The document defines the slope of a tangent line to a curve and increments. It provides definitions and rules for derivatives, including differentiation from first principles and various differentiation rules. It includes examples of finding derivatives using these rules and taking multiple derivatives.

1. Limits and Derivatives

2. Concept of a Function

3. FUNCTIONS “ FUNCTION” indicates a relationship among objects. A FUNCTION provides a model to describe a system. A FUNCTION expresses the relationship of one variable or a group of variables (called the domain) with another variables( called the range) by associating every member in the domain to a unique member in range.

4. TYPES OF FUNCTIONS LINEAR FUNCTIONS INVERSE FUNCTIONS EXPONENTIAL FUNCTIONS LOGARITHMIC FUNCTIONS

5. y is a function of x , and the relation y = x 2 describes a function. We notice that with such a relation, every value of x corresponds to one (and only one) value of y . y = x 2

6. Since the value of y depends on a given value of x , we call y the dependent variable and x the independent variable and of the function y = x 2 .

10. Notation for a Function : f ( x )

21. The Idea of Limits

22. Consider the function The Idea of Limits x 1.9 1.99 1.999 1.9999 2 2.0001 2.001 2.01 2.1 f ( x )

23. Consider the function The Idea of Limits x 1.9 1.99 1.999 1.9999 2 2.0001 2.001 2.01 2.1 f ( x ) 3.9 3.99 3.999 3.9999 un-defined 4.0001 4.001 4.01 4.1

24. Consider the function The Idea of Limits x 1.9 1.99 1.999 1.9999 2 2.0001 2.001 2.01 2.1 g ( x ) 3.9 3.99 3.999 3.9999 4 4.0001 4.001 4.01 4.1 x y O 2

25. If a function f ( x ) is a continuous at x 0 , then . approaches to, but not equal to

26. Consider the function The Idea of Limits x -4 -3 -2 -1 0 1 2 3 4 g ( x )

27. Consider the function The Idea of Limits x -4 -3 -2 -1 0 1 2 3 4 h ( x ) -1 -1 -1 -1 un-defined 1 2 3 4

28. does not exist.

29. A function f ( x ) has limit l at x 0 if f ( x ) can be made as close to l as we please by taking x sufficiently close to (but not equal to) x 0 . We write

30. Theorems On Limits

31. Theorems On Limits

32. Theorems On Limits

33. Theorems On Limits

34. Limits at Infinity

35. Limits at Infinity Consider

36. Generalized, if then

37. Theorems of Limits at Infinity

38. Theorems of Limits at Infinity

39. Theorems of Limits at Infinity

40. Theorems of Limits at Infinity

41. The Slope of the Tangent to a Curve

42. The Slope of the Tangent to a Curve The slope of the tangent to a curve y = f ( x ) with respect to x is defined as provided that the limit exists.

43. Increments The increment △ x of a variable is the change in x from a fixed value x = x 0 to another value x = x 1 .

44. For any function y = f ( x ), if the variable x is given an increment △ x from x = x 0 , then the value of y would change to f ( x 0 + △ x ) accordingly. Hence thee is a corresponding increment of y (△ y ) such that △ y = f ( x 0 + △ x ) – f ( x 0 ) .

45. Derivatives (A) Definition of Derivative. The derivative of a function y = f ( x ) with respect to x is defined as provided that the limit exists.

46. The derivative of a function y = f ( x ) with respect to x is usually denoted by

47. The process of finding the derivative of a function is called differentiation . A function y = f ( x ) is said to be differentiable with respect to x at x = x 0 if the derivative of the function with respect to x exists at x = x 0 .

48. The value of the derivative of y = f ( x ) with respect to x at x = x 0 is denoted by or .

49. To obtain the derivative of a function by its definition is called differentiation of the function from first principles .

50. Differentiation Rules 1.

51. Differentiation Rules 1.

52. Differentiation Rules 2.

53. Differentiation Rules 2.

54. Differentiation Rules 2.

55. Differentiation Rules 3.

56. Differentiation Rules 3.

57. Differentiation Rules 4. for any positive integer n

58. Differentiation Rules 4. for any positive integer n Binominal Theorem

59. Differentiation Rules 5. product rule

60. Differentiation Rules 5. product rule

62. Differentiation Rules 6. where v ≠ 0 quotient rule

63. Differentiation Rules 6. where v ≠ 0 quotient rule

65. Differentiation Rules 7. for any integer n

68. DIFFERENTIATION RULES y,u and v are functions of x. a,b,c, and n are constants (numbers). The derivative of a constant is zero. Duh! If everything is constant, that means its rate, its derivative, will be zero. The graph of a constant, a number is a horizontal line. y=c. The slope is zero. The derivative of x is 1. Yes. The graph of x is a line. The slope of y = x is 1. If the graph of y = cx, then the slope, the derivative is c.

69. MORE RULES When you take the derivative of x raised to a power (integer or fractional), you multiply expression by the exponent and subtract one from the exponent to form the new exponent. Example:

70. OPERATIONS OF DERIVATIVES The derivative of the sum or difference of the functions is merely the derivative of the first plus/minus the derivative of the second. The derivative of a product is simply the first times the derivative of the second plus second times the derivative of the first. The derivative of a quotient is the bottom times the derivative of the top, minus top times the derivative of the bottom….. All over bottom square.. TRICK: LO-DEHI – HI-DELO LO 2

71. JUST GENERAL RULES If you have constant multiplying a function, then the derivative is the constant times the derivative. See example below: The coefficient of the x 6 term is 5 (original constant) times 7 (power rule.)

72. SECOND DERIVATIVES You can take derivatives of the derivative. Given function f(x), the first derivative is f’(x). The second derivative is f’’(x), and so on and so forth. Using Leibniz notation of dy/dx For math ponders , if you are interesting in the Leibniz notation of derivatives further, please see my article on that. Thank you. Hare Krishna >=) –Krsna Dhenu

73. EXAMPLE 4: Find the derivative: Use the power rule and the rule of adding derivatives. Note 3/2 – 1 = ½. x ½ is the square root of x. Easy eh??

74. EXAMPLE 5 Find the equation of the line tangent to y = x 3 +5x 2 –x + 3 at x=0. First find the (x,y) coordinates when x = 0. When you plug 0 in for x, you will see that y = 3. (0,3) is the point at x=0. Now, get the derivative of the function. Notice how the power rule works. Notice the addition and subtraction of derivative. Notice that the derivative of x is 1, and the derivative of 3, a constant, is zero.

75. EX 5 (continued) Now find the slope at x=0, by plugging in 0 for the x in the derivative expression. The slope is -1 since f’(0) = -1. Now apply it to the equation of a line.

76. EX 5. (continued) Now, plug the x and y coordinate for x 0 and y 0 respectively. Plug the slope found in for m. And simplify On the AP, you can leave your answer as the first form. (point-slope form)

77. EXAMPLE 6 Find all the derivatives of y = 8x 5 . Just use the power rule over and over again until you get the derivative to be zero. See how the power rule and derivative notation works?