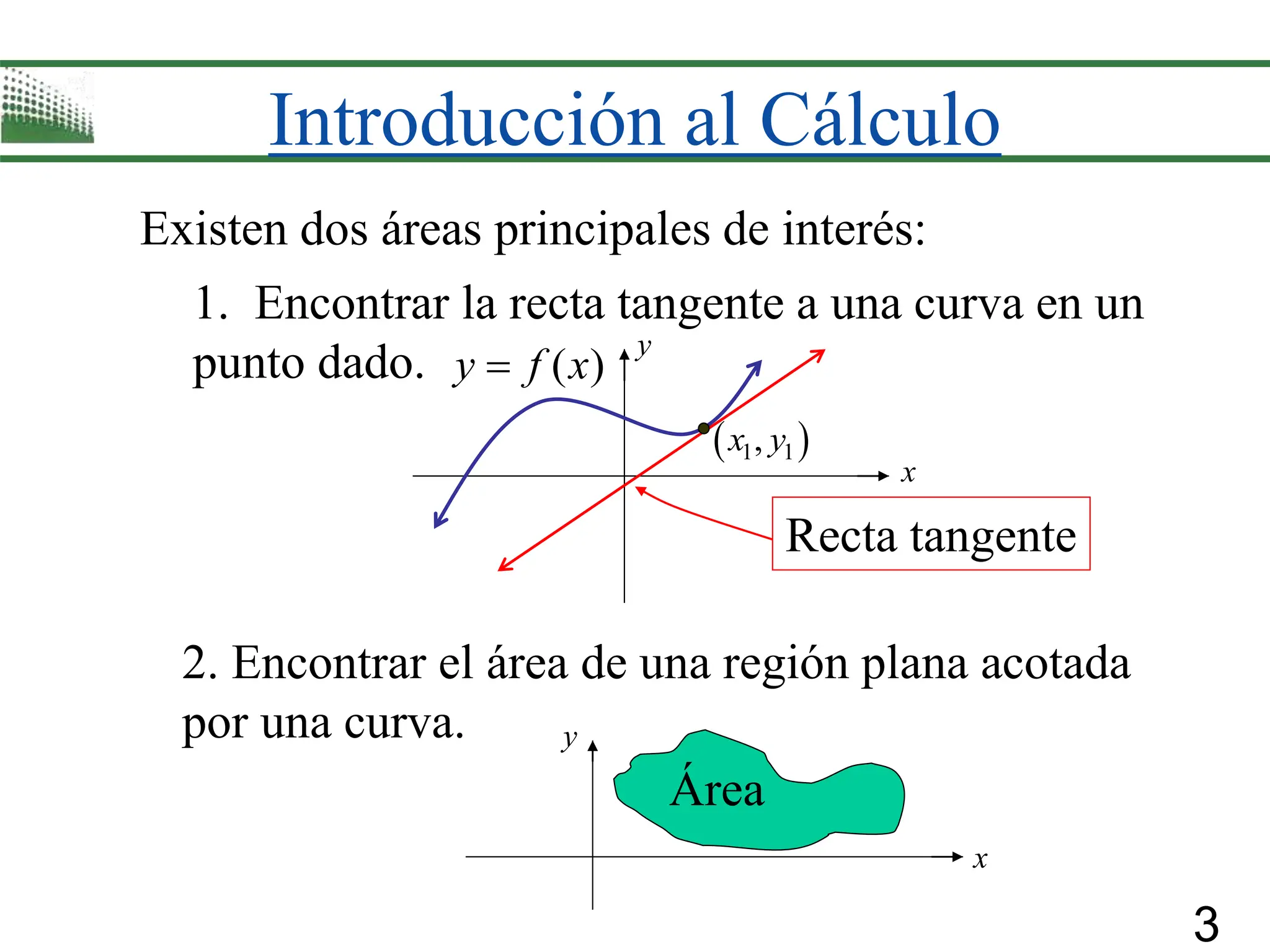
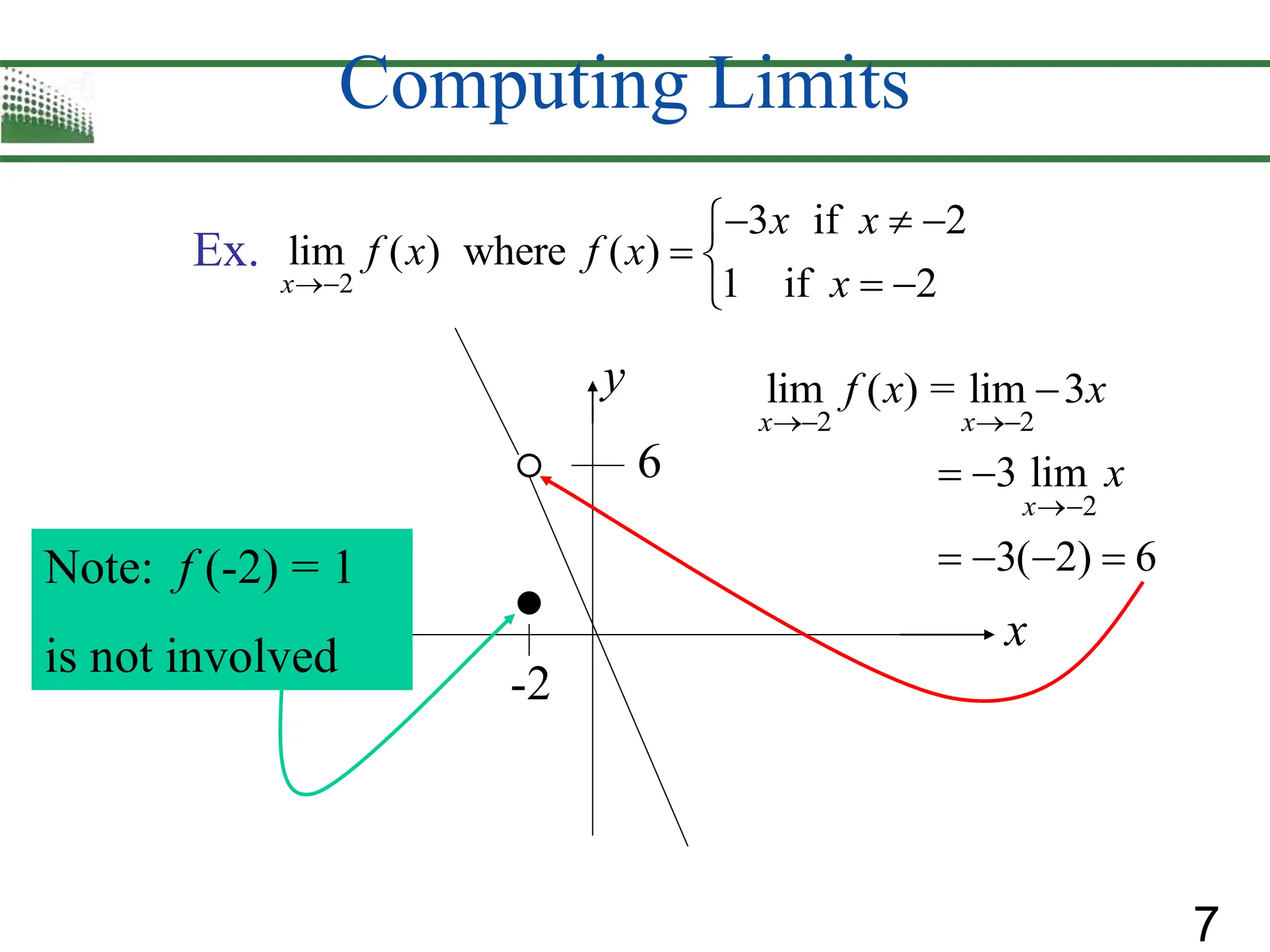
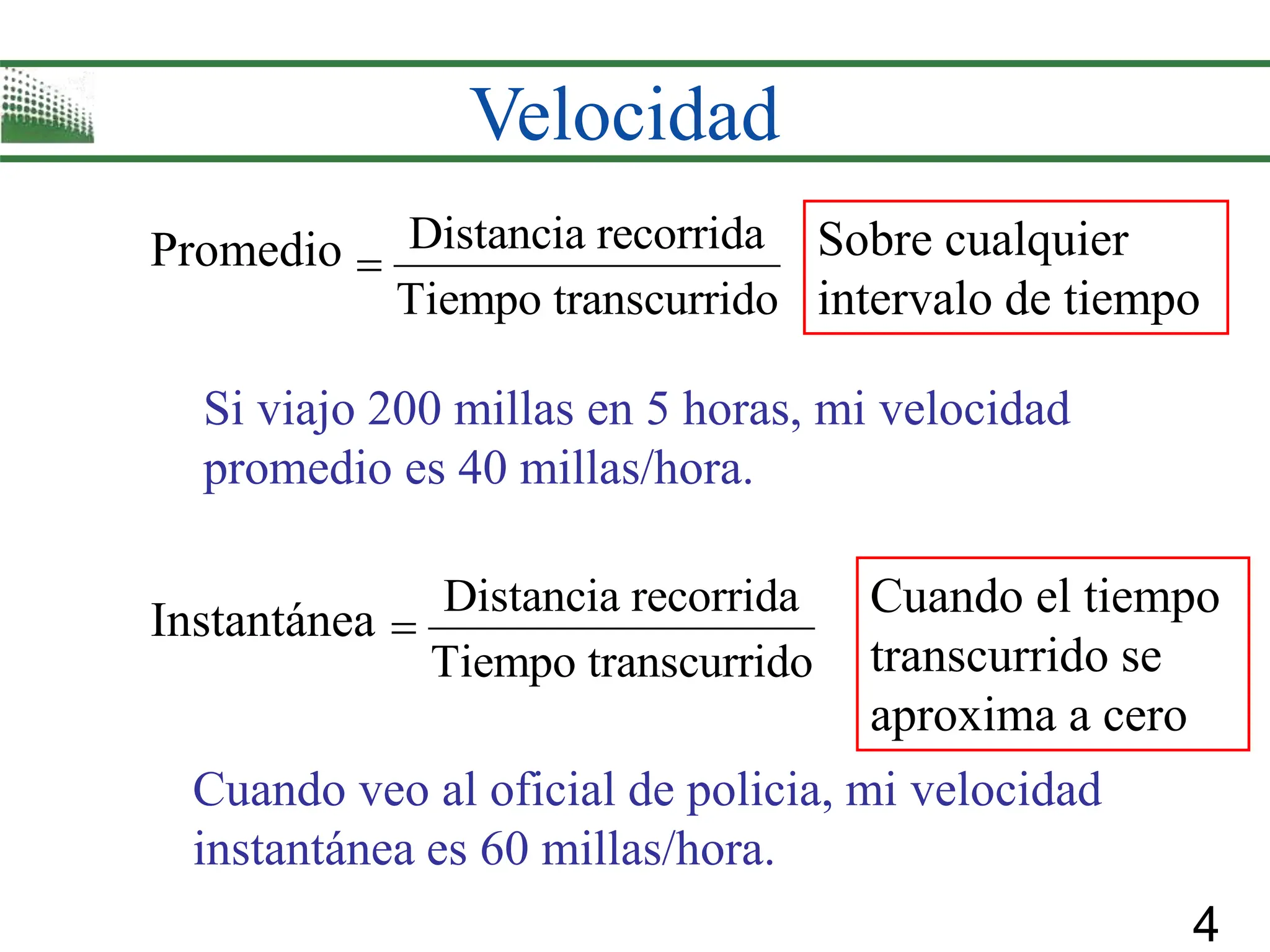
This document introduces key concepts in calculus including limits, derivatives, and rates of change. It discusses: 1) How limits describe the behavior of functions as inputs get closer to a target value. Limits are used to define continuity, derivatives, and tangent lines. 2) How derivatives measure the instantaneous rate of change of a function and are defined as the limit of the average rate of change over infinitesimally small intervals. 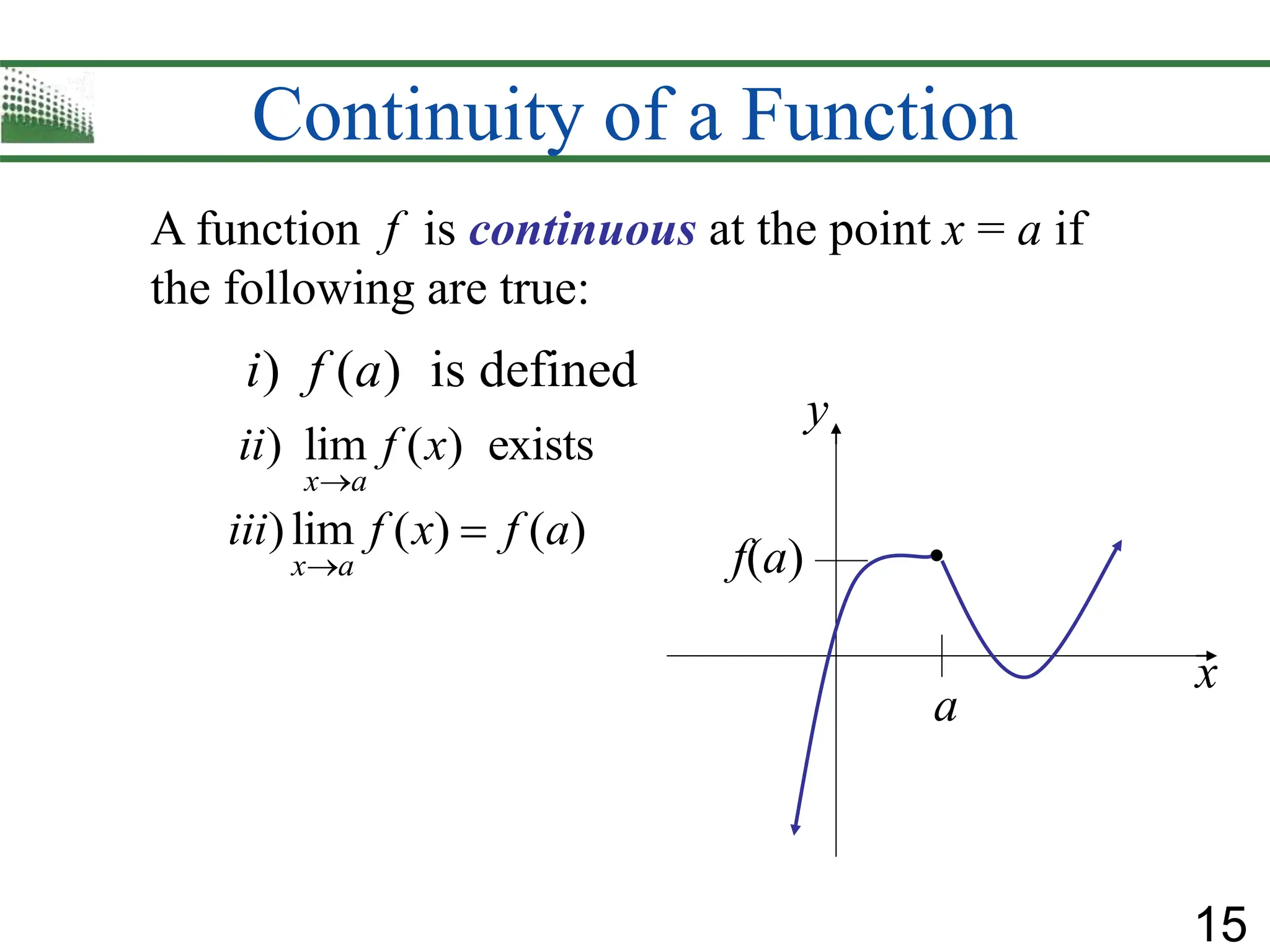3) Properties of continuous functions including that polynomials, rational functions, and basic operations preserve continuity. The intermediate value theorem and existence of zeros are introduced.

1. 1
4
Límites y
Derivadas

2. 2
Límites y la Derivada
• Límites
• Límites Laterales
• Continuidad
• La Derivada

3. 3
Introducción al Cálculo
Existen dos áreas principales de interés:
1. Encontrar la recta tangente a una curva en un
punto dado. ( )
y f x

Recta tangente
 
1 1
,
x y
2. Encontrar el área de una región plana acotada
por una curva.
Área
x
x
y
y

4. 4
Velocidad
Promedio Distancia recorrida
Tiempo transcurrido

Instantánea Cuando el tiempo
transcurrido se
aproxima a cero
Sobre cualquier
intervalo de tiempo
Si viajo 200 millas en 5 horas, mi velocidad
promedio es 40 millas/hora.
Cuando veo al oficial de policia, mi velocidad
instantánea es 60 millas/hora.
Distancia recorrida
Tiempo transcurrido


5. 5
Velocidad
Ej. Given the position function   2
10
s t t t
 
where t is in seconds and s(t) is measured in
feet, find:
a. The average velocity for t = 1 to t = 3.
b. The instantaneous velocity at t = 1.
ave
(3) (1) 39 11
Velocity 14 ft/sec
3 1 2
s s
 
  

Average velocity
t
( ) (1)
1
s t s
t


1.1 12.1
1.001 12.001
1.01 12.01
Answer: 12 ft/sec

Notice how
elapsed time
approaches zero

6. 6
Límite de una Funcción
The limit of f (x), as x approaches a, equals L
written:
if we can make the value f (x) arbitrarily close
to L by taking x to be sufficiently close to a.
lim ( )
x a
f x L


a
L
( )
y f x

x
y

7. 7
Computing Limits
Ex.
2
3 if 2
lim ( ) where ( )
1 if 2
x
x x
f x f x
x

  

 
 

6
-2
2 2
lim ( ) = lim 3
x x
f x x
 

2
3 lim
3( 2) 6
x
x

 
   
Note: f (-2) = 1
is not involved
x
y

8. 8
Properties of Limits
 
 
 
Suppose lim ( ) and lim ( )
Then,
1. lim ( ) , real number
2. lim ( ) lim ( ) , real number
3. lim ( ) ( )
4. lim ( ) ( )
lim ( )
( )
5. lim
( ) lim
x a x a
r r
x a
x a x a
x a
x a
x a
x a
f x L g x M
f x L r a
cf x c f x cL c a
f x g x L M
f x g x LM
f x
f x
g x
 

 




 

 
  

 Provided that 0
( )
x a
L
M
g x M

 

9. 9
Computing Limits
Ex.
Ex.
 
2
3
lim 1
x
x


2
3 3
lim lim1
x x
x
 
 
 
2
3 3
2
lim lim1
3 1 10
x x
x
 
 
  
1
2 1
lim
3 5
x
x
x



 
 
1
1
lim 2 1
lim 3 5
x
x
x
x





1 1
1 1
2lim lim1
3lim lim5
x x
x x
x
x
 
 



2 1 1
3 5 8

 


10. 10
Indeterminate Form:
0
0
2
5
5
lim
25
x
x
x



Ex. Notice form
0
0
  
5
5
lim
5 5
x
x
x x



 
 
5
1 1
lim
5 10
x x

 
 
Factor and cancel
common factors

11. 11
Limits at Infinity
For all n > 0,
1 1
lim lim 0
n n
x x
x x
 
 
provided that is defined.
1
n
x
Ex.
2
2
3 5 1
lim
2 4
x
x x
x

 

2
2
5 1
3
lim
2
4
x
x x
x

 


3 0 0 3
0 4 4
 
  

Divide
by 2
x
2
2
5 1
lim 3 lim lim
2
lim lim 4
x x x
x x
x x
x
  
 
   
 
   
   

 

 
 

12. 12
One-Sided Limit of a Function
The right-hand limit of f (x), as x approaches a,
equals L
written:
if we can make the value f (x) arbitrarily close
to L by taking x to be sufficiently close to the
right of a.
lim ( )
x a
f x L



a
L
( )
y f x


13. 13
One-Sided Limit of a Function
The left-hand limit of f (x), as x approaches a,
equals M
written:
if we can make the value f (x) arbitrarily close
to M by taking x to be sufficiently close to the
left of a.
lim ( )
x a
f x M



a
M
( )
y f x

x
y

14. 14
One-Sided Limit of a Function
2
if 3
( )
2 if 3
x x
f x
x x
 

 



Ex. Given
3
lim ( )
x
f x


3 3
lim ( ) lim 2 6
x x
f x x
 
 
 
2
3 3
lim ( ) lim 9
x x
f x x
 
 
 
Find
Find
3
lim ( )
x
f x



15. 15
Continuity of a Function
A function f is continuous at the point x = a if
the following are true:
) ( ) is defined
i f a
) lim ( ) exists
x a
ii f x

)lim ( ) ( )
x a
iii f x f a


a
f(a)
y
x

16. 16
Properties of Continuous Functions
The constant function f (x) is continuous everywhere.
Ex. f (x) = 10 is continuous everywhere.
The identity function f (x) = x is continuous
everywhere.

17. 17
Properties of Continuous Functions
A polynomial function y = P(x) is continuous at
everywhere.
A rational function is continuous
at all x values in its domain.
( )
( )
( )
p x
R x
q x

If f and g are continuous at x = a, then
 
, , and ( ) 0 are continuous
at .
f
f g fg g a
g
x a
 


18. 18
Intermediate Value Theorem
If f is a continuous function on a closed interval [a, b]
and L is any number between f (a) and f (b), then there
is at least one number c in [a, b] such that f(c) = L.
( )
y f x

a b
f (a)
f (b)
L
c
f (c) =
x
y

19. 19
Intermediate Value Theorem
 
2
Given ( ) 3 2 5. Show that ( ) 0
has at least one solution on 1, 2 .
f x x x f x
   
Ex.
(1) 4 0 and (2) 3 0
f f
    
f (x) is continuous for all values of x and since
f (1) < 0 and f (2) > 0, by the Intermediate Value
Theorem, there exists a c on (1, 2) such that
f (c) = 0.

20. 20
Existence of Zeros of a Continuous
Function
If f is a continuous function on a closed interval [a, b],
and f(a) and f(b) have opposite signs, then there is at least
one solution of the equation f(x) = 0 in the interval (a, b).
f(b)
f(a)
a
b
x
y

21. 21
Example
(Existence of zeros of a continuous function)
1. Show that f(x) is a continuous function everywhere.
The function is a polynomial function and is
therefore continuous everywhere.
2. Show that f(x) = 0 has at least one solution on the
interval (0, 2)
Since (0) 5 and (2) 5 have opposite signs,
there must be at least one number with
0 2 such that ( ) 0.
f f
x c
c f c
  

  
2
Let ( ) 3 5.
f x x x
  

22. 22
Rates of Change
Average rate of change of f over the interval
[x, x+h]
( ) ( )
f x h f x
h
 

Instantaneous rate of change of f at x
Slope of the
Tangent Line
Slope of Secant Line
0
( ) ( )
lim
h
f x h f x
h

 


23. 23
The Derivative
0
( ) ( )
( ) lim
h
f x h f x
f x
h

 
 
The derivative of a function f with respect to x is
the function ,
f  given by
It is read “f prime of x.”

24. 24
The Derivative
0
( ) ( )
( ) lim
h
f x h f x
f x
h

 
 
Four-step process for finding :
f 
( ) ( )
f x h f x
 
( ) ( )
f x h f x
h
 
( )
f x h

1. Compute
2. Find
3. Find
4. Compute

25. 25
The Derivative
 
2
0 0
0
( ) ( ) 4 2
lim lim
lim 4 2 4
h h
h
f x h f x xh h
h h
x h x
 

  

   
Given
2 2 2
( ) ( ) 2 4 2 1 (2 1)
f x h f x x xh h x
       
2
( ) ( ) 4 2
f x h f x xh h
h h
  

 2 2 2
( ) 2 1 2 4 2 1
f x h x h x xh h
       
1.
2.
3.
4.
2
( ) 2 1, find ( ).
f x x f x

 
2
4 2
xh h
 
( ) 4
f x x
 

26. 26
Example
Find the slope of the tangent line to the
graph of at any
point (x, f(x)).
Step 1.
Step 2.
Step 3.
Step 4.
( ) 2( ) 3 2 2 3
f x h x h x h
        
( ) ( ) 2
2
f x h f x h
h h
  
  
( ) 2 3
f x x
  
( ) ( ) ( 2 2 3) ( 2 3) 2
f x h f x x h x h
          
 
0 0
( ) ( )
( ) lim lim 2 2
h h
f x h f x
f x
h
 
 
     

27. 27
Differentiability and Continuity
If a function is differentiable at x = a, then it is
continuous at x = a.
Not
Differentiable
Not
Continuous
Still
Continuous
x
y

28. 28
Example
The function is not
differentiable at x = 0 but it is continuous
everywhere.
( )
f x x

x
y
O
( )
f x x


29. 29
Axiomas de Probabilidad
Dado un espacio muestral W , la probabilidad P de un
evento A es un número real no negativo P(A), que debe
satisfacer los tres axiomas siguientes:
• Límites
• Límites Laterales
• Continuidad
• La Derivada

30. 30