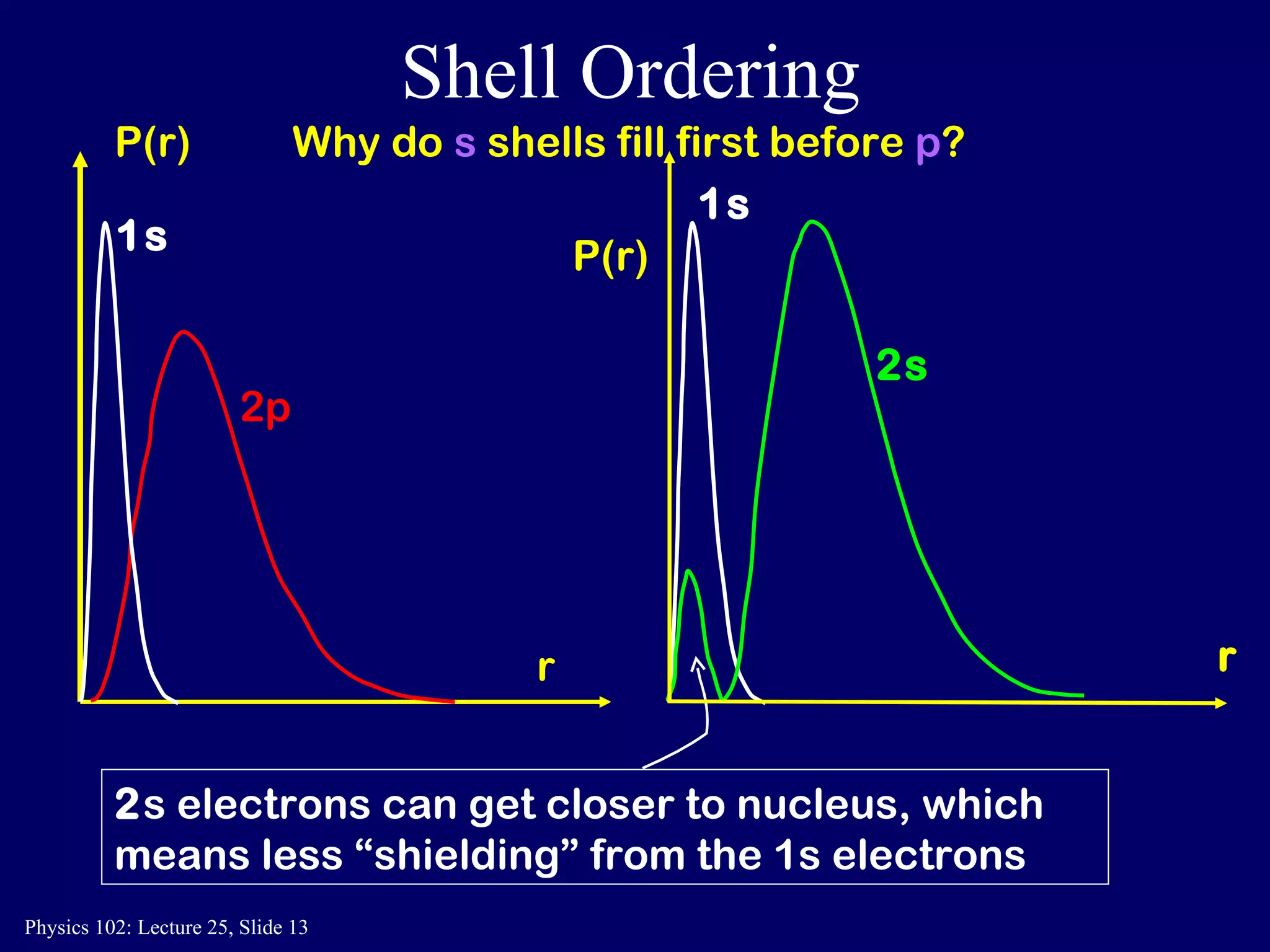
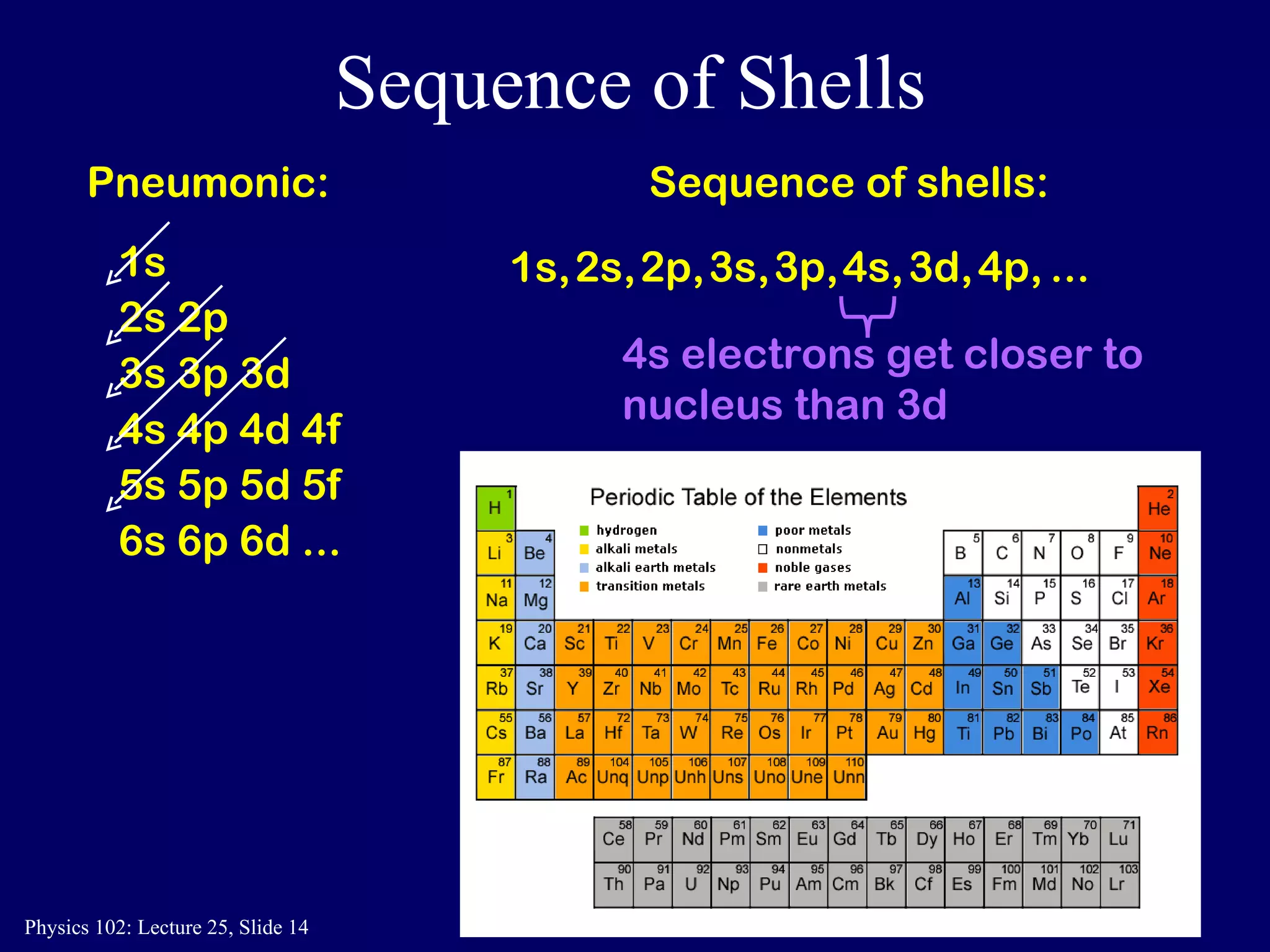
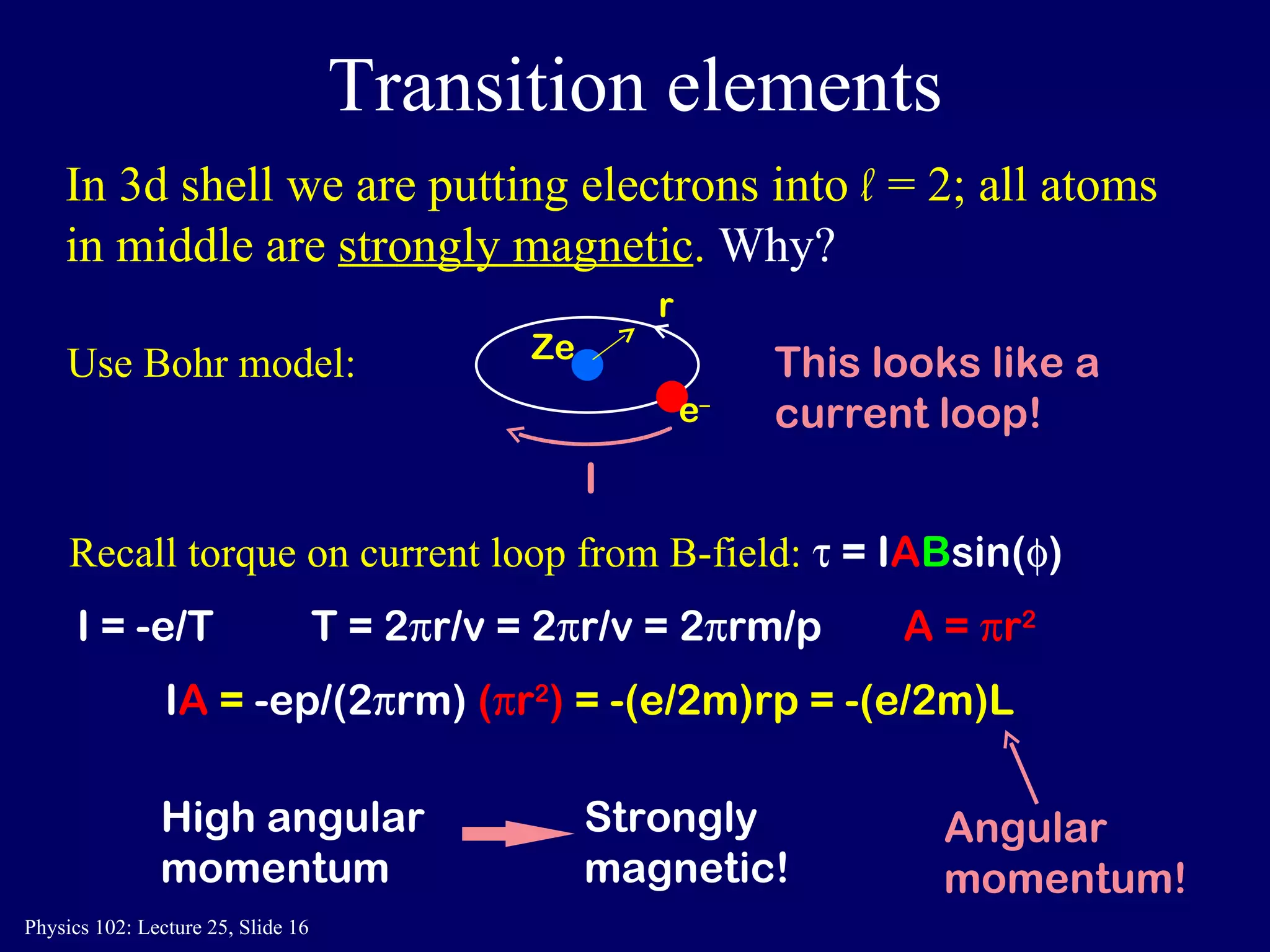
The document discusses the quantum numbers that describe the electron states in an atom. It explains that each electron is labeled by four quantum numbers: principal (n), angular momentum (l), magnetic (ml), and spin (ms). The Pauli Exclusion Principle states that each quantum state can contain only one electron, which explains the filling order and structure of the periodic table.

1. Periodic Table, Atomic Structure Physics 102: Lecture 25

2. From last lecture – Bohr model L n = nh /2 π Angular momentum is quantized Energy is quantized Radius is quantized n = 1, 2, 3 ... Linear momentum too Bohr model is incorrect!

3. Quantum Numbers Each electron in an atom is labeled by 4 #’s Note differences with Bohr model n = Principal Quantum Number (1, 2, 3, …) Determines energy (Bohr) m s = Spin Quantum Number (-½ , +½) “ Up Spin” or “Down Spin” l = Orbital Quantum Number (0, 1, 2, … n-1) Determines angular momentum l < n always true! m l = Magnetic Quantum Number (- l , … 0, … l ) Component of l | m l | <= l always true!

4. ACT: Quantum numbers For which state of hydrogen is the orbital angular momentum required to be zero? 1. n=1 2. n=2 3. n=3

5. Spectroscopic Nomenclature l =0 is “ s state ” l =1 is “ p state ” l =2 is “ d state ” l =3 is “ f state ” l =4 is “ g state ” 1 electron in ground state of Hydrogen: n=1, l =0 is denoted as: 1s 1 “ Subshells ” “ Shells ” n =1 is “ K shell ” n =2 is “ L shell ” n =3 is “ M shell ” n =4 is “ N shell ” n =5 is “ O shell ” Example n=1 l =0 1 electron

6. Electron orbitals In correct quantum mechanical description of atoms, positions of electrons not quantized, orbitals represent probabilities

7. Quantum Numbers How many unique electron states exist with n=2 ? l = 0 : m l = 0 : m s = ½ , -½ 2 states l = 1 : m l = +1: m s = ½ , -½ 2 states m l = 0: m s = ½ , -½ 2 states m l = -1: m s = ½ , -½ 2 states 2s 2 2p 6 There are a total of 8 states with n=2 Example

8. ACT: Quantum Numbers How many unique electron states exist with n=5 and m l = +3 ? A) 0 B) 4 C) 8 D) 16 E) 50

9. Preflight 25.2 What is the maximum number of electrons that can exist in the 5g (n=5, l =4) subshell of an atom?

10. Pauli Exclusion Principle In an atom with many electrons only one electron is allowed in each quantum state (n, l , m l , m s ). This explains the periodic table!

11. Electron Configurations Atom Configuration H 1s 1 He 1s 2 Li 1s 2 2s 1 Be 1s 2 2s 2 B 1s 2 2s 2 2p 1 Ne 1s 2 2s 2 2p 6 1s shell filled 2s shell filled 2p shell filled etc (n=1 shell filled - noble gas) (n=2 shell filled - noble gas) p shells hold up to 6 electrons s shells hold up to 2 electrons

12. The Periodic Table What determines the sequence? Pauli exclusion & energies s ( l =0) p ( l =1) d ( l =2) f ( l =3) n = 1, 2, 3, ... Also s

13. Shell Ordering Why do s shells fill first before p ? r 2p P(r) 2 s electrons can get closer to nucleus, which means less “shielding” from the 1s electrons r 2s P(r) 1s 1s

14. Sequence of Shells Sequence of shells: 1s 2s 2p 3s 3p 3d 4s 4p 4d 4f 5s 5p 5d 5f 6s 6p 6d ... 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, Pneumonic: ... 4s electrons get closer to nucleus than 3d

15. Properties of elements We can understand the different properties of elements from the periodic table Example Noble gases Filled outer p-shell (s for He) Hard to ionize Non-reactive Alkali metals Unpaired outer s-shell e – Easy to ionize Very reactive Transition metals Filling d-shell ( l = 2) Tend to be magnetic s 2 p 6 s 1 d 1 – d 10

16. Transition elements Recall torque on current loop from B-field:  = I A B sin(  ) I A = -ep/(2  rm) (  r 2 ) = -(e/2m)rp = -(e/2m)L T = 2  r/v = 2  r/v = 2  rm/p In 3d shell we are putting electrons into l = 2; all atoms in middle are strongly magnetic . Why? High angular momentum Strongly magnetic! Use Bohr model: Ze e – This looks like a current loop! I = -e/T A =  r 2 r I Angular momentum!

17. Sodium Na 1s 2 2s 2 2p 6 3s 1 Many spectral lines of Na are outer electron making transitions www.WebElements.com Example Yellow line of Na flame test is 3p 3s Neon - like core Single outer electron

18. Summary Each electron state labeled by 4 numbers: n = principal quantum number (1, 2, 3, …) l = angular momentum (0, 1, 2, … n-1) m l = component of l (- l < m l < l ) m s = spin (-½ , +½) Pauli Exclusion Principle explains periodic table Shells fill in order of lowest energy.