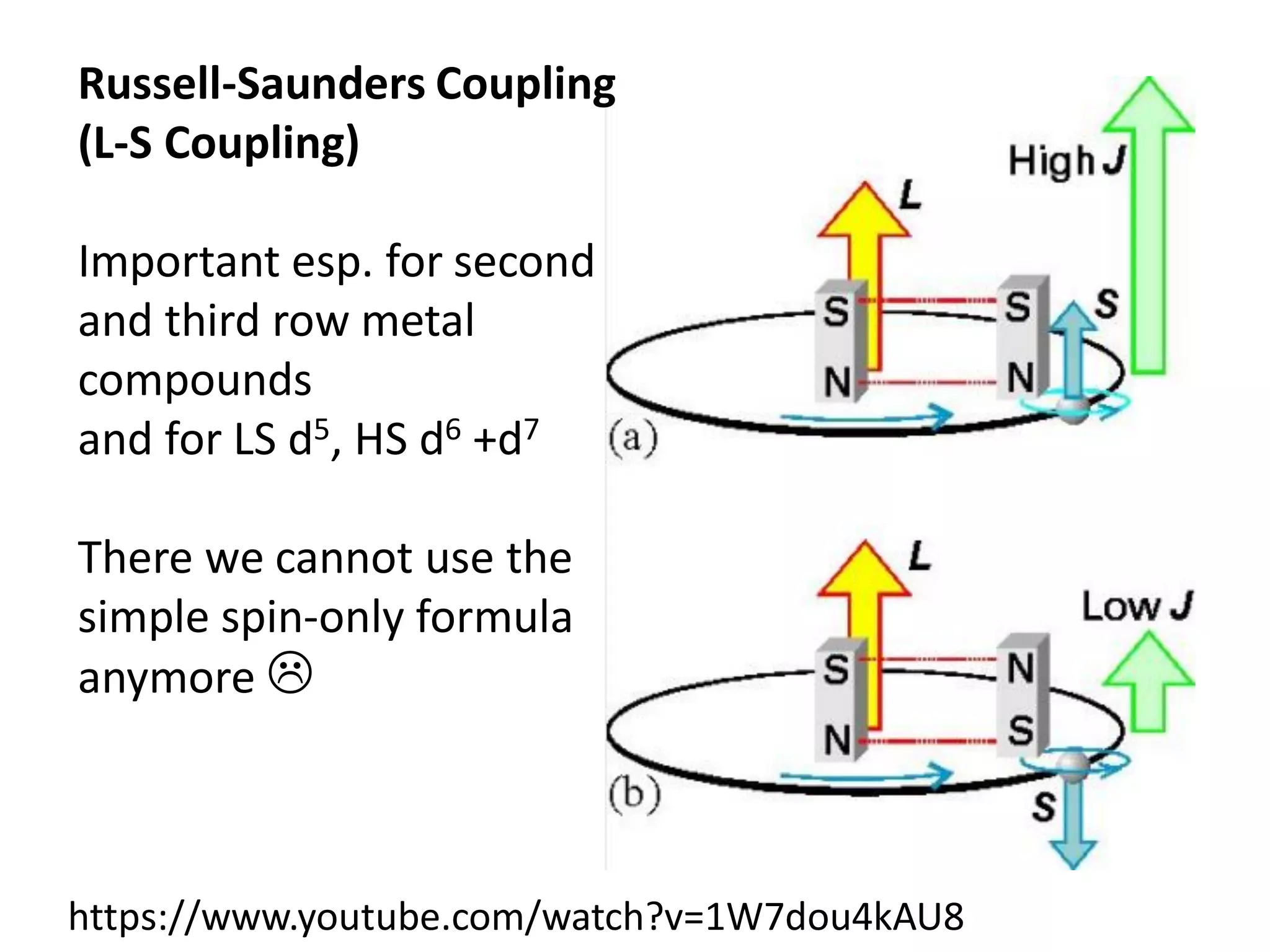
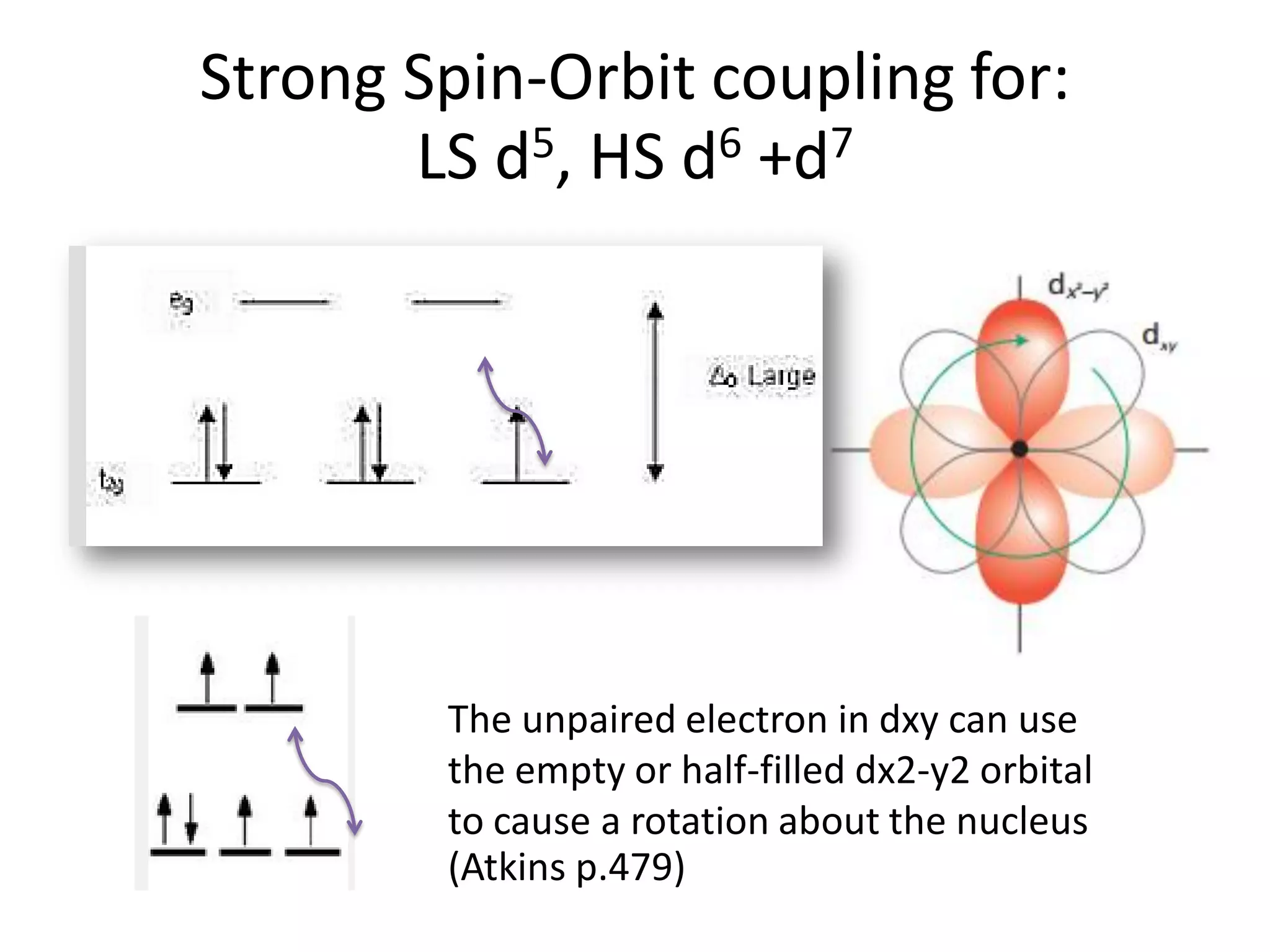
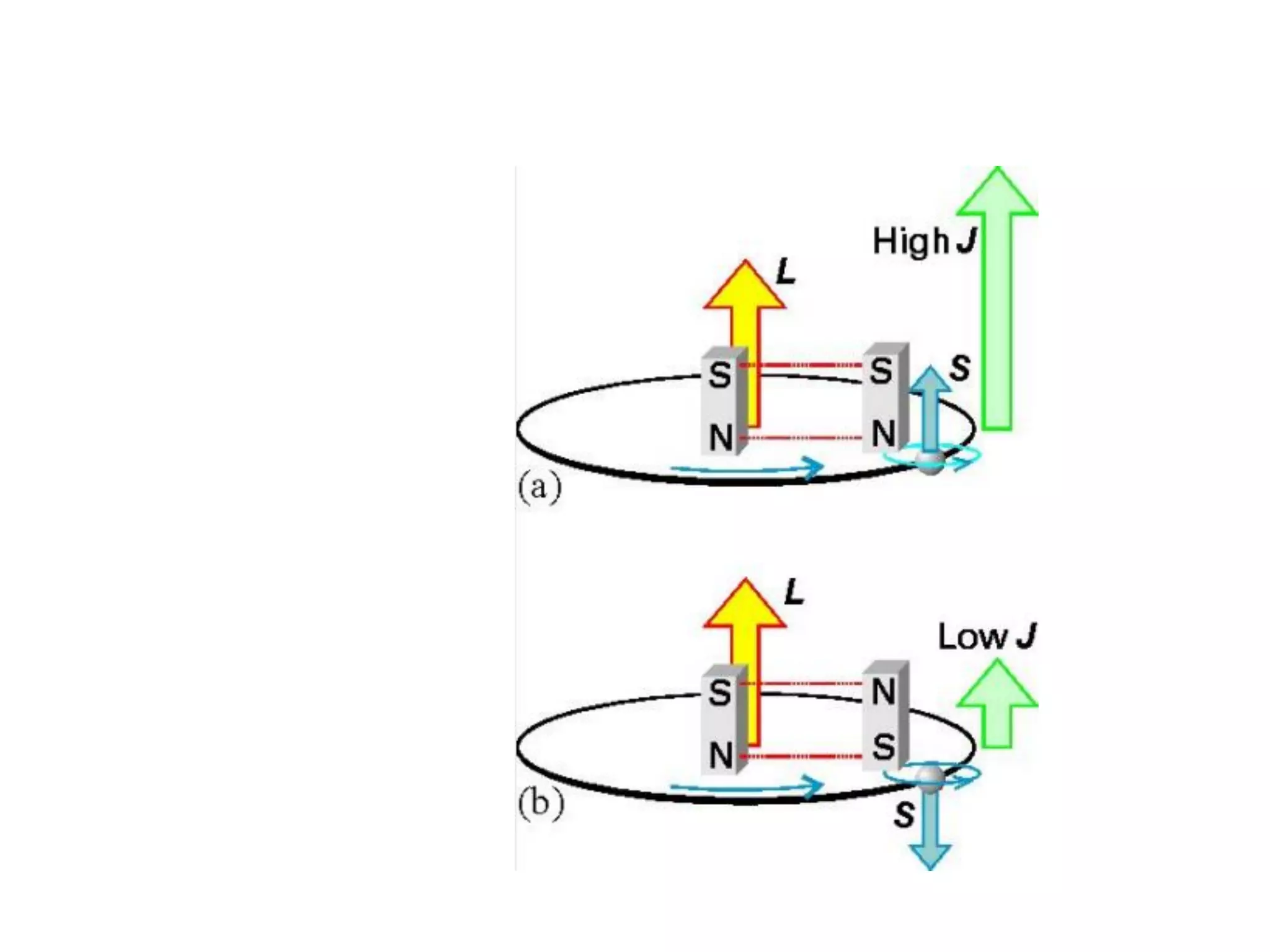
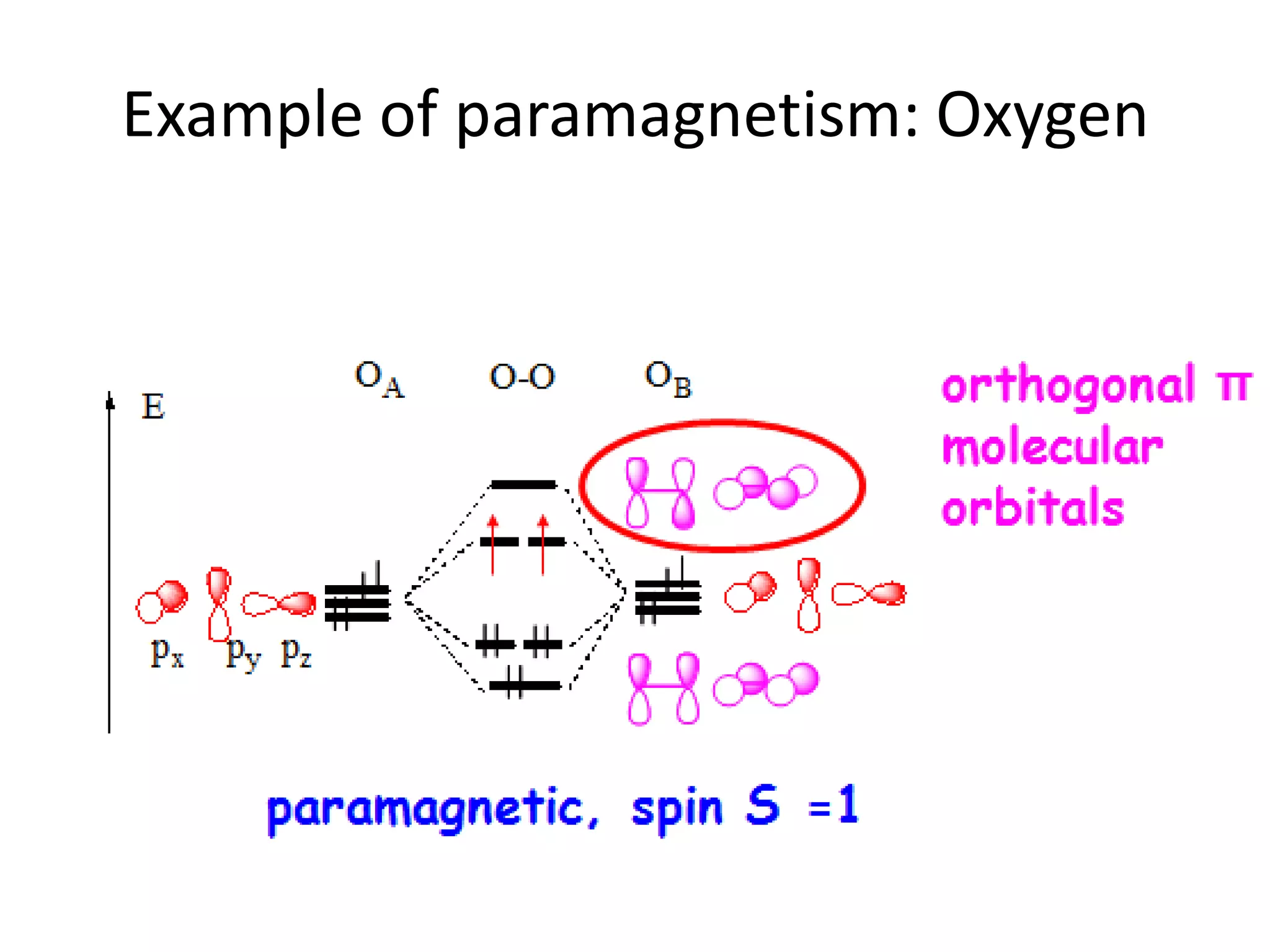
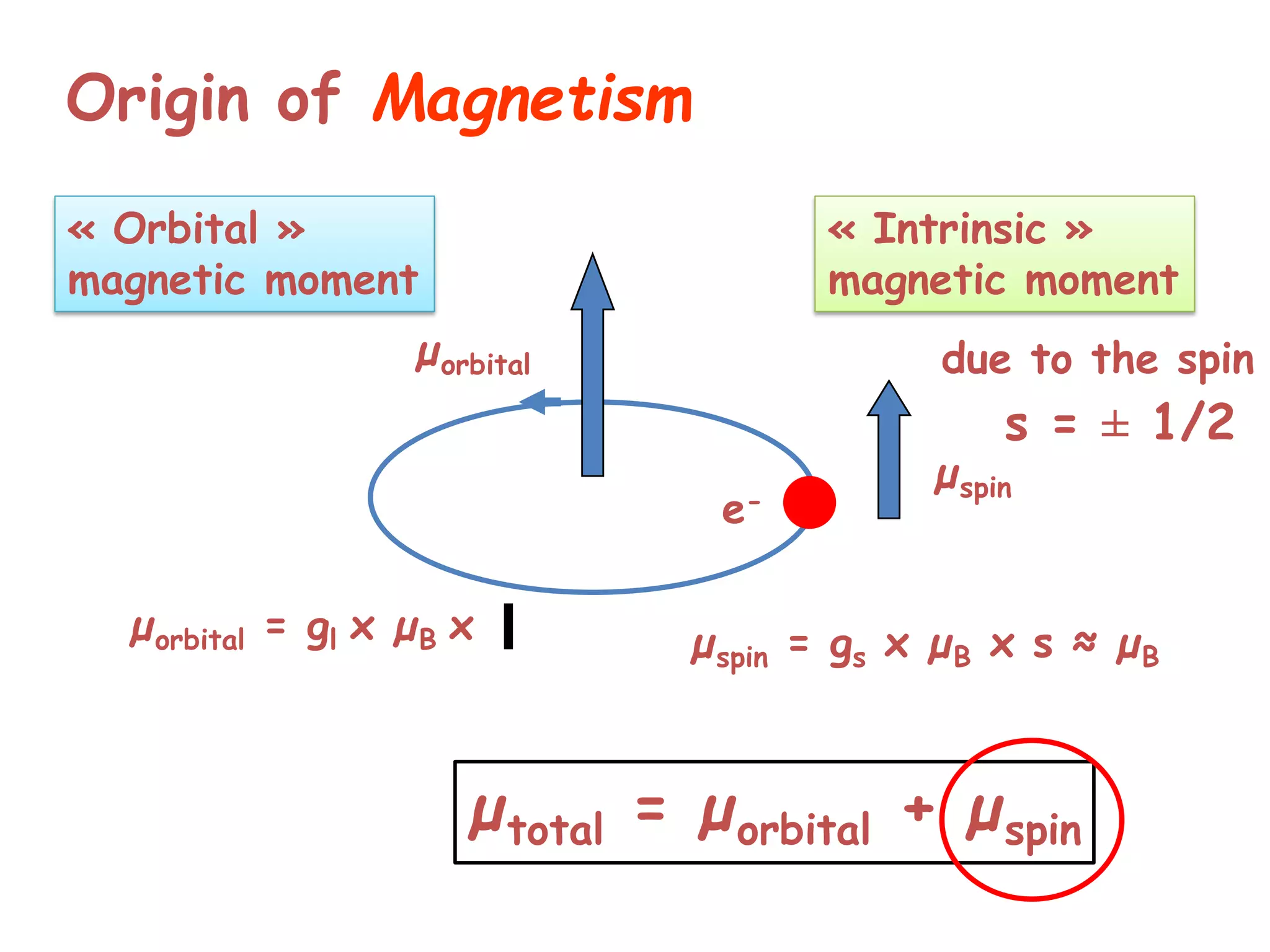
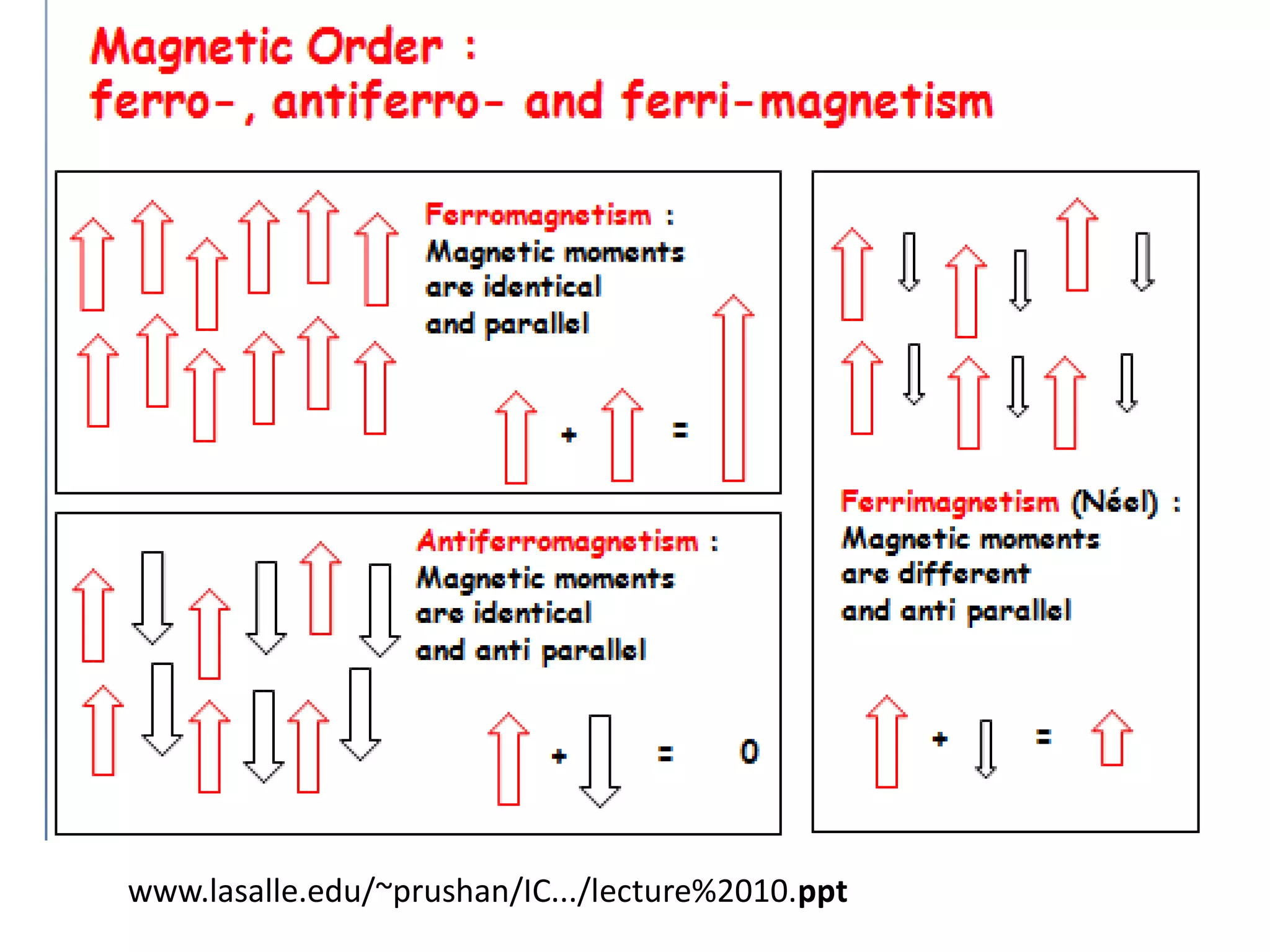
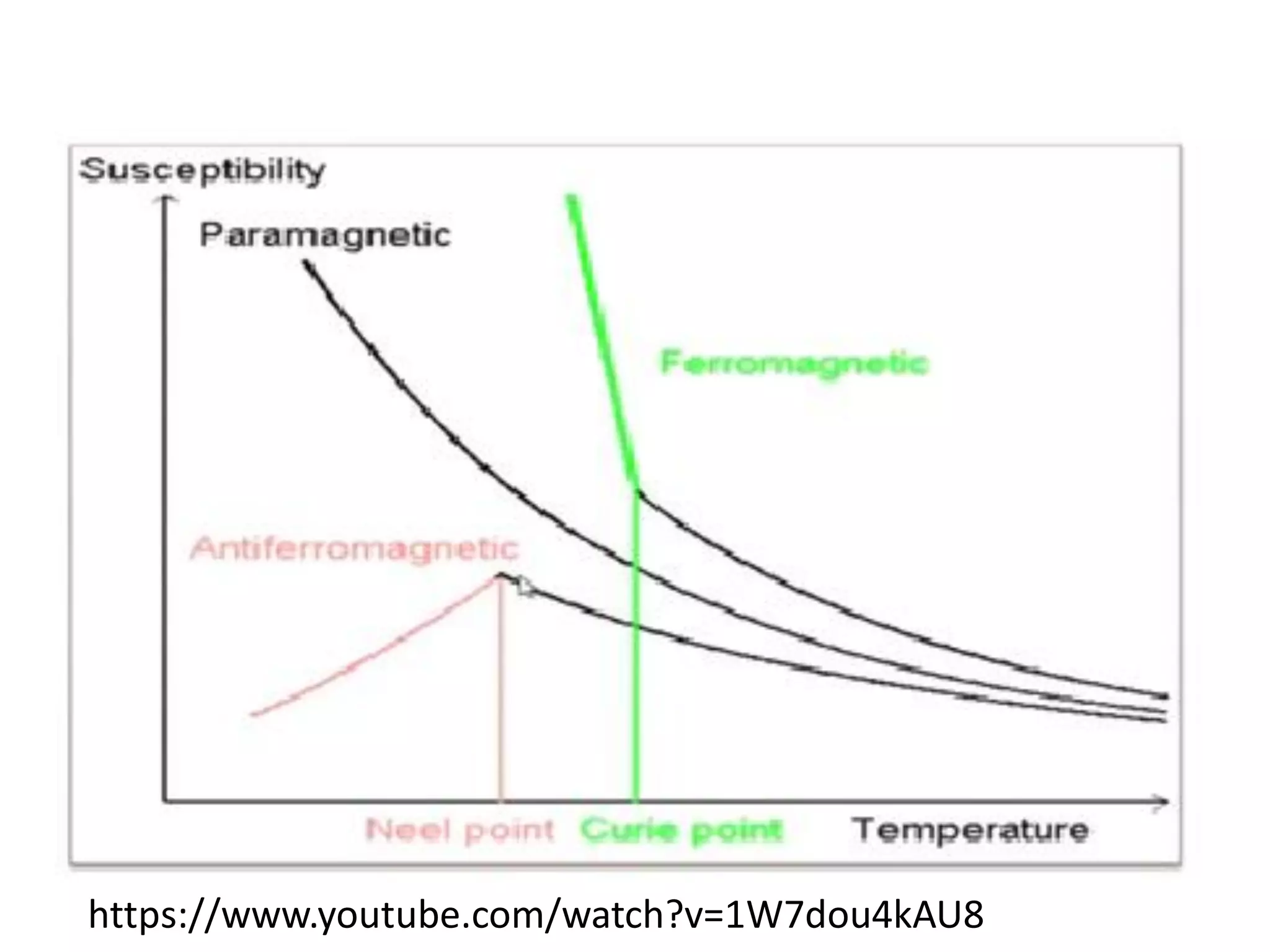
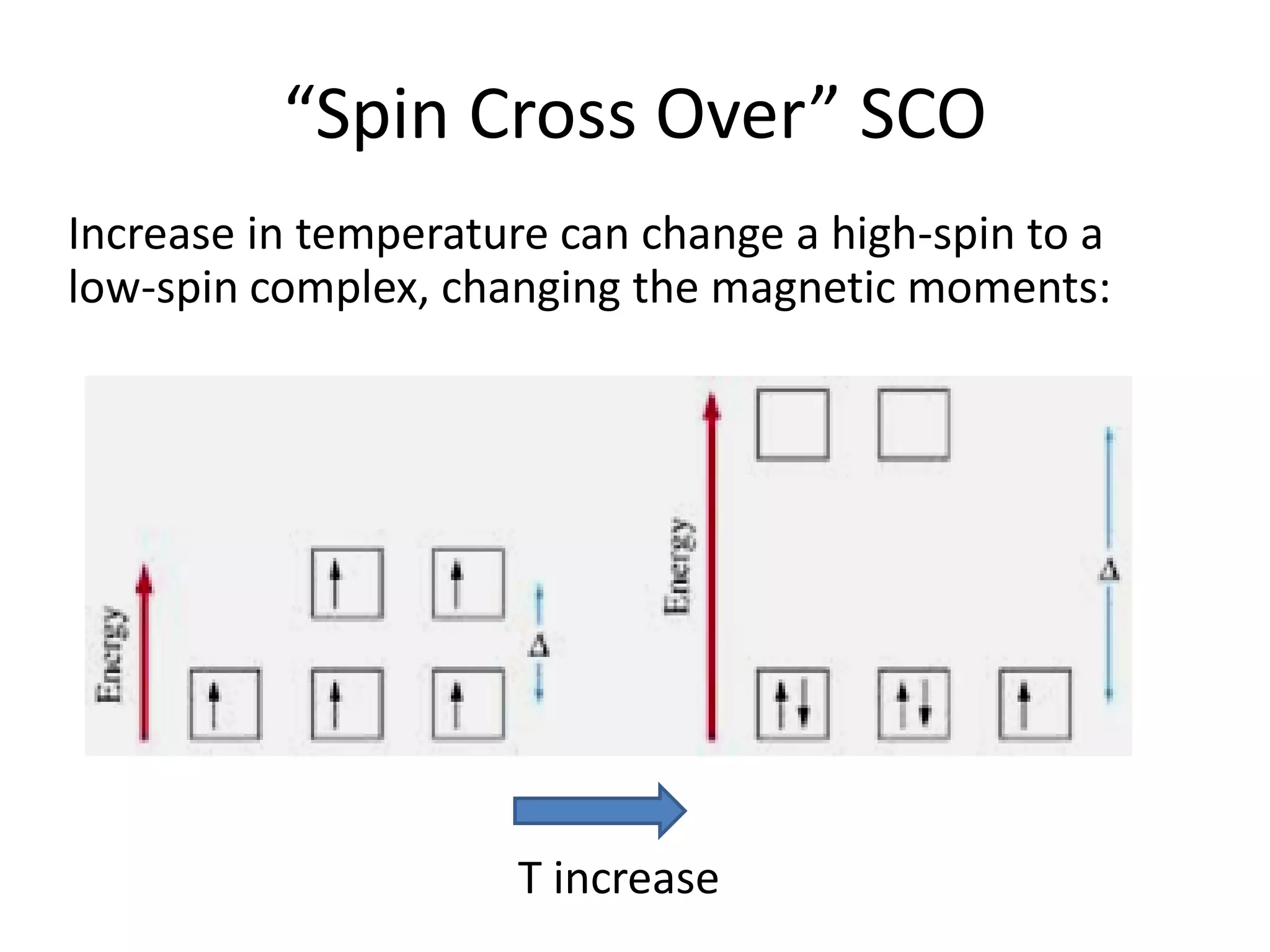
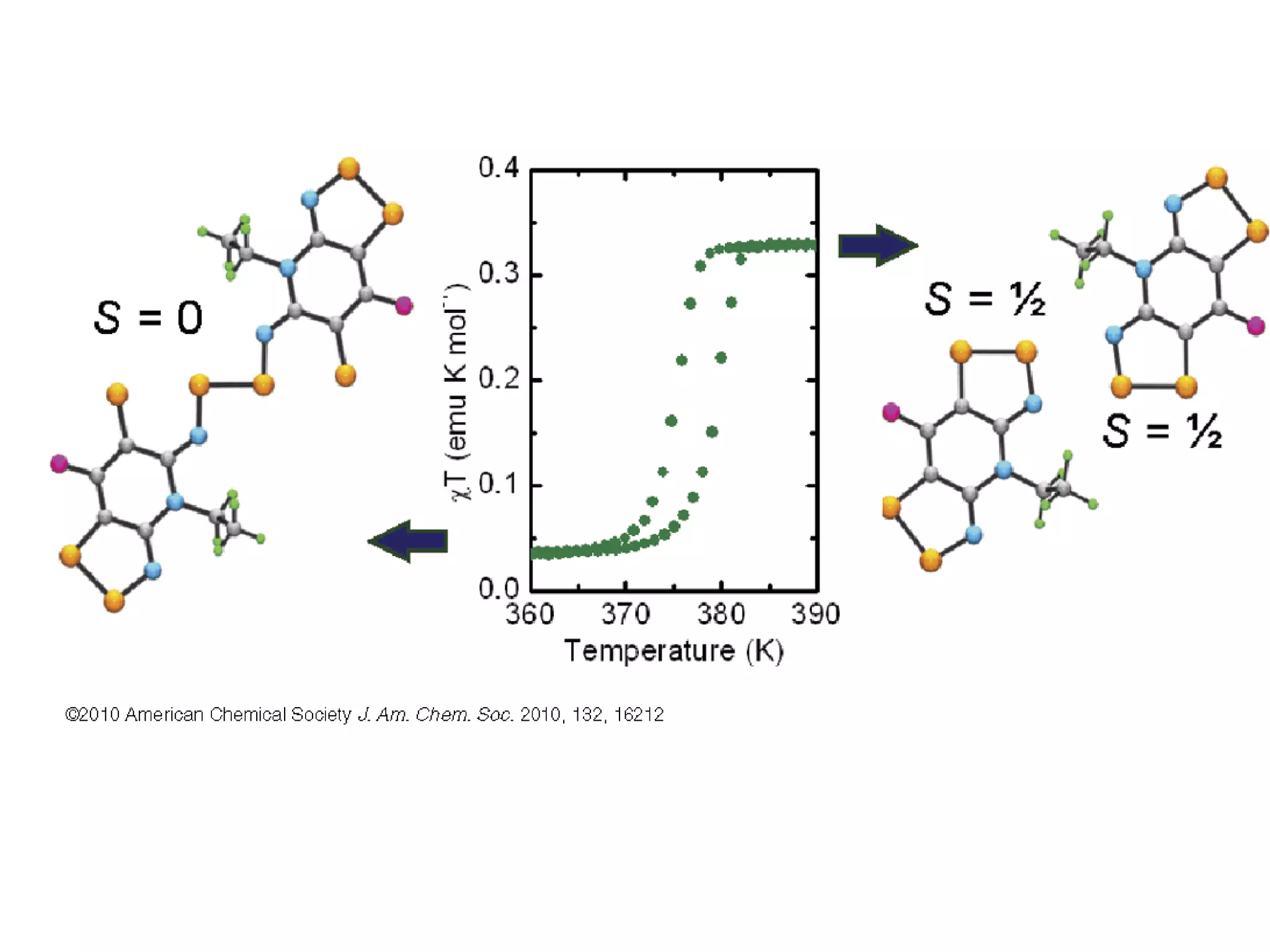
Paramagnetism arises from unpaired electrons in coordination compounds. Each unpaired electron contributes a magnetic moment due to both its spin and orbital angular momentum. When an external magnetic field is applied, the magnetic moments of paramagnetic compounds can align, causing the compound to become temporarily magnetic. The magnetic susceptibility and magnetization of paramagnetic compounds increases with applied field strength and decreases with increasing temperature according to Curie's law. Some transition metal complexes can switch between low-spin and high-spin electronic configurations in response to temperature changes, altering their magnetic properties.

1. Properties of coordination
compounds
Part 2 (2/3)
Magnetism
(extensive explanations:
http://nptel.ac.in/courses/104105033/30)
All Tables and Examples from:
Shriver & Atkins
Inorganic Chemistry, 5th Ed.

2. Review Spinels

3. “normal Spinel” vs. “inverse Spinel”
Ni(II) Mn(III)2O4 Mn(III) [Ni(II)Mn(III)] O4
2 Mn3+ in Oh:
= d4 HS
CFSE= 3*(-2/5o) + 3/5o
= -12.600 cm-1
For 2 Mn ->
-25.200 cm-1
(tetrahedral Ni(II):
E = 4*(-3/5 t) + 4*(2/5 t)
= -4/5 t = -4/5 * 0.44 * o
= -3000 cm-1 )
1 Mn3+ in Oh:
= d4 HS
CFSE= -12.600 cm-1
1 Ni2+ in Oh:
= d8 HS
CFSE= 6*(-2/5 o)+ 2*(3/5o)
= (-12/5 + 6/5)o (+ 3P)
= -6/5 o = -10.200 cm-1
-> total: 22.800 cm-1
(tetrahedral Mn(III):
E = 2*(-3/5t) + 2*(2/5t)
= = -2/5 t = -2/5 * 0.44 * o
= -3700 cm-1 )
=> We can look only on the
octahedral configurations
to decide !

4. http://www.youtube.com/watch?v=u36QpPvEh2c
Dia- and Para-Magnetism

5. Magnetic Properties
Paramagnetism arises from unpaired electrons.
Each electron has a magnetic moment with
one component associated with the spin
angular momentum of the electron and
(except when the quantum number l ¼0) a
second component associated with the orbital
angular momentum.
(p.579)

6. Where does magnetism come from ?
https://www.youtube.com/watch?v=qfooM_Gl69k

7. Effect of unpaired electrons
http://www.youtube.com/watch?v=qfooM_Gl69k

8. Example of paramagnetism: Oxygen

9. Gouy Balance

10. http://wwwchem.uwimona.edu.jm/utils/gouy.html

11. Origin of Magnetism
e-
« Orbital »
magnetic moment
« Intrinsic »
magnetic moment
due to the spin
µspin = gs x µB x s ≈ µB
s = ± 1/2
µorbital = gl x µB x l
µtotal = µorbital + µspin
µorbital
µspin

12. www.lasalle.edu/~prushan/IC.../lecture%2010.ppt

13. Para-magnetism
Atoms that have unpaired electrons (also metals) and
therefore a total electron-spin S.
These individual magnetic moments can be oriented by
an outer magnetic field to line up.
Paramagnetic substances are not magnetic by
themselves but can become magnetic when an outer
field is applied.
Every ferromagnetic material has a Curie-Temperature
Tc where it loses its permanent magnets and becomes
para-magnetic.

14. Curies Law
Describes the “magnetic susceptibility” of a
material dependent on the outer field B and
Temperature T
=> High magnetization M:
(a) High external field B
(b) Low temperature
Or: ‘chi”
= magn.
susceptibility

15. Curies Temperature Tc
Heating up a permanent magnet brings the spins to
become randomly oriented (at temperature Tc)
-> the material loses its magnetism but can still
become magnetic again in an external field

16. https://www.youtube.com/watch?v=1W7dou4kAU8

17. Spin-only formula

18. Examples

19. Conclusions from magn. susceptibility

20. Find the electron configuration from the following
observations:
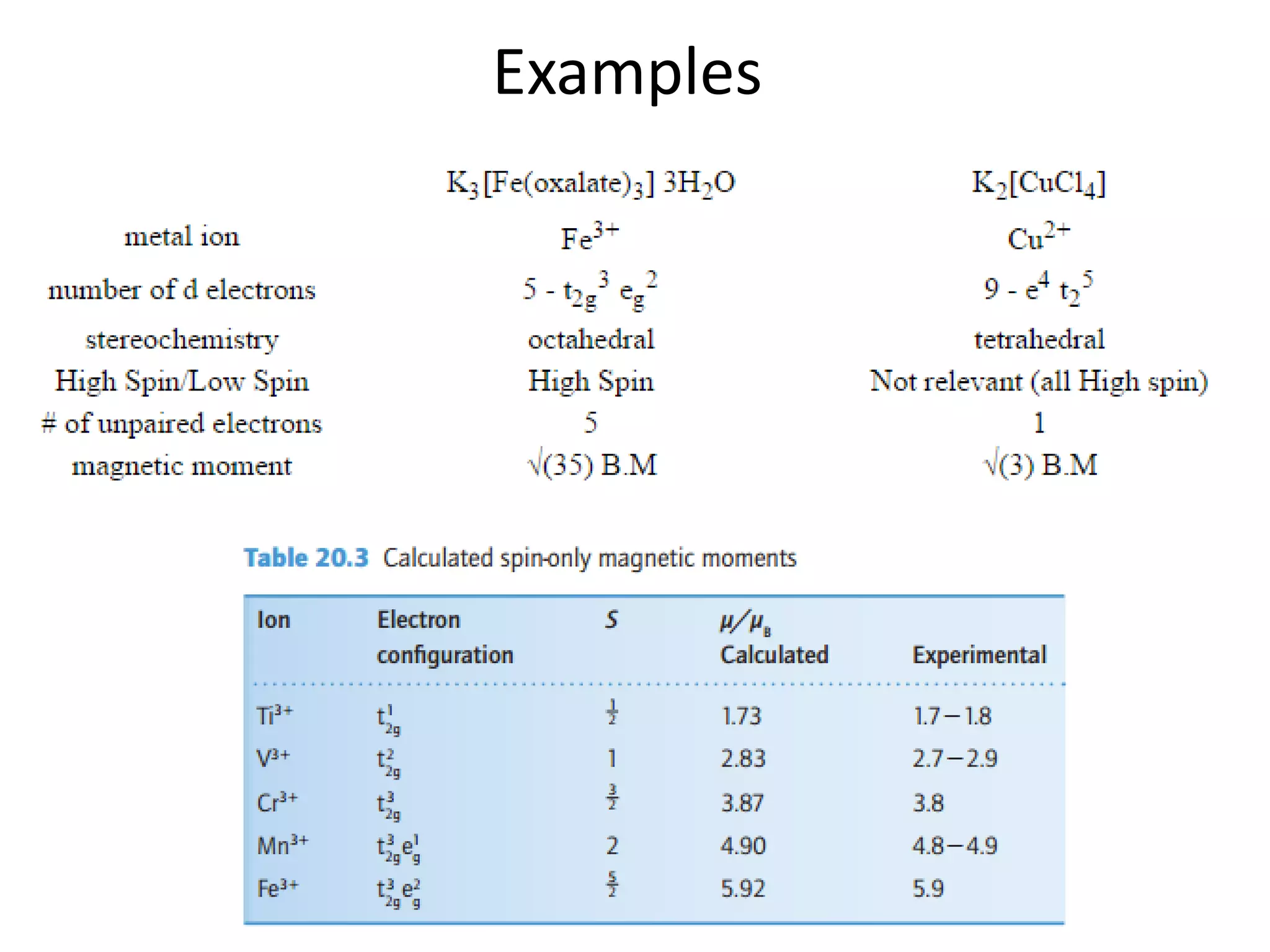
(a) μeff for [Cr(NH3)6]Cl2 is 4.85 μB.
(b) μeff for [V(NH3)6]Cl2 is 3.9 μB.
(c) μeff for a Co(II) complex is 4.0 μB.
(d) μeff for [Mn(NCS)6]4(-) is 6.06 μB.

22. Spin Cross Over SCO
Some complexes can change from low-spin to high-
spin at higher temperatures:
=> low magnetic moment -> high m.m.
=> M-L bonds short -> longer
(why ?)
This can happen quickly in a small T-range
http://www.youtube.com/watch?v=e9SMMA9Xe9c

23. “Spin Cross Over” SCO
Increase in temperature can change a high-spin to a
low-spin complex, changing the magnetic moments:
T increase

24. SCO applications

26. Spin and orbital contributions to the
magnetic moment
If S-L coupling is weak

27. Deviations from spin-only formula
Example:
[Fe(CN)6]3- has μ = 2.3μB
which is between low- and high-spin calculated
(check this out)

28. Russell-Saunders Coupling
(L-S Coupling)
Important esp. for second
and third row metal
compounds
and for LS d5, HS d6 +d7
There we cannot use the
simple spin-only formula
anymore 
https://www.youtube.com/watch?v=1W7dou4kAU8

29. Strong Spin-Orbit coupling for:
LS d5, HS d6 +d7
The unpaired electron in dxy can use
the empty or half-filled dx2-y2 orbital
to cause a rotation about the nucleus
(Atkins p.479)

30. Spin-orbitcoupling
Is higher than spin-only – typical for d-complexes
with more than half-filled d-shell

31. Info to solve problems:

32. Spin-Orbit coupling
Russell-Saunders Coupling

34. Electronic states review
Alternative to state the electron configuration of
an ion as 4s2 3d6, we can express this
configuration as “microstates”:
Ti(3+):
4s0 3d1
Microstates:
S = ½
L = 2 (“d”)
=> J = 5/2, 3/2 ( L+S),(L+S-1),…(L-S)
Ground State with lowest J: 2D3/2

37. Examples

39. Atkins p.505