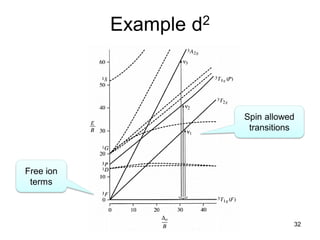
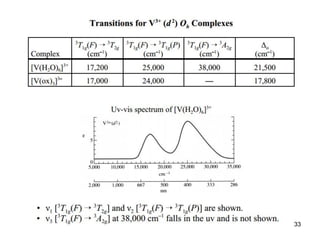
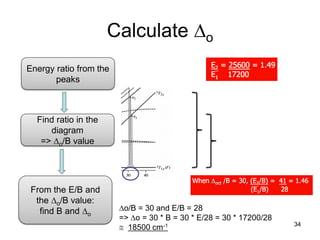
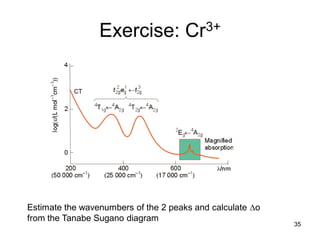
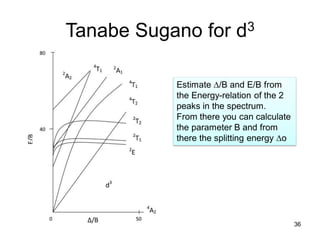
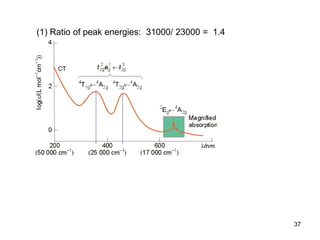
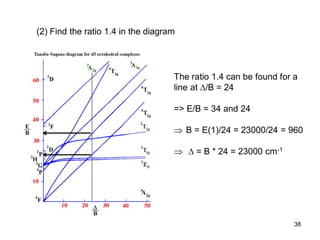
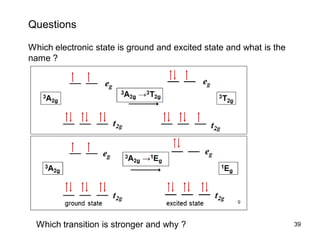
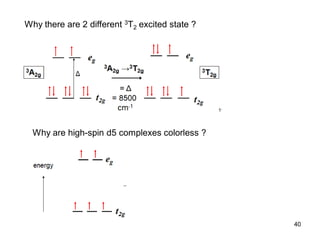
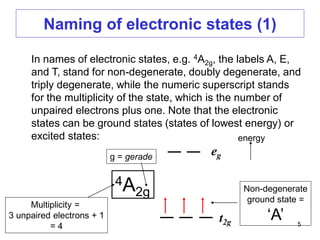
The document discusses UV-Vis spectroscopy of transition metal compounds, focusing on d-block metal ion complexes and their electronic spectra. It covers the nomenclature of electronic states, selection rules for electronic transitions, and the intensity of d-d transitions, emphasizing the differences between octahedral and tetrahedral complexes. Additionally, it introduces concepts such as vibronic coupling and Tanabe-Sugano diagrams for analyzing electronic transitions and calculating splitting energies.

1. UV-VIS Spectroscopy
Transition Metal
Compounds
Part 1 of
Spectroscopic Methods in Inorganic Chemistry
1

2. The electronic spectra of d-block complexes:
The features of electronic spectra that we need to be
able to master are:
1) naming of electronic states and d-d transitions,
e.g.3A2g, or 3A2g→1Eg
2) Explanation of relative intensities of bands in the
spectra of complexes of d-block metal ions.
(The Laporte and spin selection rules)
3) calculation of the crystal field splitting parameters
from energies of d-d bands
2

3. Introduction
d1 VIS Spectra
d1 Spectra 2
Composite Colors
3

4. d-d spectra and MO theory:
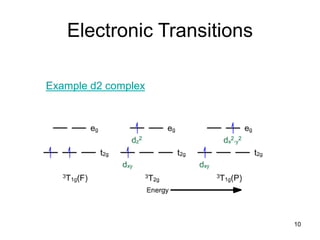
3A2g →3T2g
3A2g →1Eg
υ, cm-1
UV
[Ni(NH3)6]2+
visible infrared
4

5. Naming of electronic states (1)
In names of electronic states, e.g. 4A2g, the labels A, E,
and T, stand for non-degenerate, doubly degenerate, and
triply degenerate, while the numeric superscript stands
for the multiplicity of the state, which is the number of
unpaired electrons plus one. Note that the electronic
states can be ground states (states of lowest energy) or
excited states:
4A2g
t2g
eg
Multiplicity =
3 unpaired electrons + 1
= 4
Non-degenerate
ground state =
‘A’
g = gerade
energy
5

6. 6
Naming of electronic states (2)
The suffixes are products of symmetry elements:

7. Products
https://www.webqc.org/symmetrypointgroup-oh.html
7

8. eg
eg eg
t2g t2g
6A2g
3T2g
1A2g
Non-degenerate triply degenerate non-degenerate
Multiplicity
= 5 + 1
energy
t2g
Naming of electronic states (3)
NOTE: In determining degeneracy, one can re-arrange the electrons, but
the number of unpaired electrons must stay the same, and the number
of electrons in each of the eg and t2g levels must stay the same.
Multiplicity
= 2 + 1
Multiplicity
= 0 + 1 8

9. eg
eg eg
t2g t2g
5Eg
5T2g
2Eg
eg
eg eg
t2g t2g
3A2g
1Eg
3T2g
Naming of electronic states (contd.):
t2g
t2g
ground state excited state excited state
ground state excited state ground state
energy
9

10. Electronic Transitions
Example d2 complex
10

11. Electronic transitions for Ni2+
eg
eg
eg
eg
t2g t2g
t2g t2g
3A2g →3T2g
3A2g →1Eg
3A2g
3T2g
3A2g
1Eg
ground state excited state 11

12. visible infraredUV
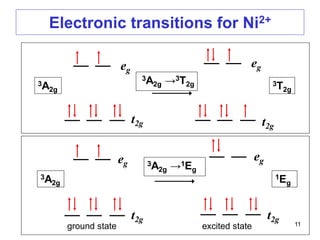
green
3A2g →3T2g
3A2g →1Eg
[Ni(H2O)6]2+
The electronic spectrum of [Ni(H2O)6]2+:
λ,
The complex looks green, because it absorbs only weakly at 500 nm,
the wavelength of green light.
12

13. On the previous slide we saw the two bands due to the
3A2g →3T2g and 3A2g →1Eg transitions. The band at λ =
1180 nm which is the 3A2g →3T2g transition shown below,
corresponds to Δ for the complex. This is usually
expressed as Δ in cm-1 = (1/λ(nm)) x 107 = 8500 cm-1.
The electronic spectrum of [Ni(H2O)6]2+:
eg
eg
t2g t2g
3A2g →3T2g3A2g
3T2gΔ
= Δ
= 8500
cm-1
13

14. Note the weak band at 620 nm that corresponds to the
3A2g →1Eg transition. The electron that is excited moves
within the eg level, so that the energy does not involve Δ,
but depends on the value of P, the spin-pairing energy.
The point of interest is why this band is so weak, as
discussed on the next slide.
The electronic spectrum of [Ni(H2O)6]2+:
eg
eg
t2g t2g
3A2g →1Eg3A2g
1EgΔ
= 16100
cm-1
14

15. The electronic spectrum of [Ni(H2O)6]2+:
The two peaks at higher energy resemble the 3A2g→3T2g transition, but
involve differences in magnetic quantum numbers of the d-orbitals,
and are labeled as 3A2g→3T1g(F) and 3A2g→3T1g(P) to reflect this:
3A2g →3T2g
3A2g →3T1g(F)
3A2g →3T1g(P)
3A2g →1Eg
λ,
[Ni(H2O)6]2+
15

16. Selection Rules
16
1

17. 17
All transitions within the d-shell, such as 3A2g→3T2g are Laporte
forbidden, because they are g→g. Thus, the intensity of the d-d
transitions that give d-block metal ions their colors are not very
intense.
Charge transfer bands frequently involve p→d or d→p
transitions, and so are Laporte-allowed and therefore very
intense.
2

18. 18

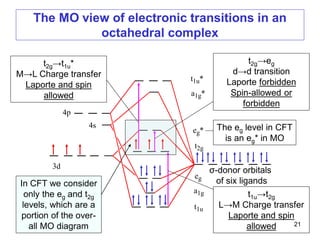
19. The Selection rules for electronic transitions
3A2g →3T2g
Charge-transfer band – Laporte and spin allowed – very intense
[Ni(H2O)6]2+
a
b c
3A2g →1Eg Laporte and spin forbidden – very weak
a, b, and c, Laporte
forbidden, spin
allowed, inter-
mediate intensity
19

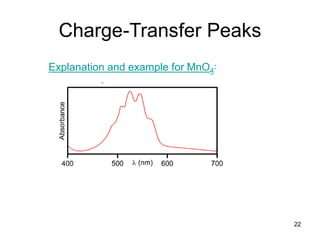
20. The three types of bands present in e.g. [Ni(H2O)6]2+ are:
1) Laporte-allowed plus spin allowed charge transfer
bands of very high intensity
2) Laporte-forbidden plus spin-allowed d→d transitions
(e.g. 3A2g→3T2g) of moderate intensity
3) Laporte forbidden plus spin-forbidden d→d transitions
(3A2g→1Eg) of very low intensity.
The Intensity of bands in complexes of d-block ions:
20

21. The MO view of electronic transitions in an
octahedral complex
t1u*
a1g*
eg*
t2g
t1u
eg
4p
4s
a1g
3d
t2g→t1u*
M→L Charge transfer
Laporte and spin
allowed
t1u→t2g
L→M Charge transfer
Laporte and spin
allowed
t2g→eg
d→d transition
Laporte forbidden
Spin-allowed or
forbidden
The eg level in CFT
is an eg* in MO
In CFT we consider
only the eg and t2g
levels, which are a
portion of the over-
all MO diagram
σ-donor orbitals
of six ligands
21

22. Charge-Transfer Peaks
Explanation and example for MnO4
-
22

23. There are two mechanisms that allow ‘forbidden’
electronic transitions to become somewhat ‘allowed’.
These are:
1) Mixing of states: The states in a complex are never
pure, and so some of the symmetry properties of
neighboring states become mixed into those of the
states involved in a ‘forbidden’ transition.
2) Vibronic Coupling: Electronic states are always
coupled to vibrational states. The vibrational states may
be of opposite parity to the electronic states, and so help
overcome the Laporte selection rule.
Why do we see ‘forbidden’ transitions at all?
23

24. Mixing of states: Comparison of [Ni(H2O)6]2+ and [Ni(en)3]2+:
[Ni(H2O)6]2+
[Ni(en)3]2+
3A2g →3T2g
3A2g →3T2g(F)
The spin-forbidden 3A2g →1Eg is close to the spin-allowed
3A2g →3T2g(F) and ‘borrows’ intensity by mixing of states
The spin-forbidden 3A2g →1Eg is not close
to any spin allowed band and is very weak
3A2g →1Eg
Note: The two spectra are
drawn on the same graph
for ease of comparison.
24

25. Electronic transitions are coupled to vibrations of various
symmetries, and the latter may impart opposite parity to
an electronic state and so help overcome the Laporte
selection rule:
Vibronic coupling:
electronic ground
state is ‘g’
electronic excited
state is ‘g’
g→g transition
is forbidden
g→(g+u) transition
is allowed
energy
coupled vibration
υ4’ is ‘u’
Electronic transitions, as seen
in the spectra of complexes of
Ni(II) shown above, are always
very broad because they are
coupled to vibrations. The
transitions are thus from ground
states plus several vibrational
states to excited states plus
several vibrational states (υ1, υ2, υ3),
so the ‘electronic’ band is actually
a composite of electronic plus
vibrational transitions.
υ5
υ3
υ1
υ5’
υ3’
υ1’
25

26. Symmetry of vibrational states, and their
coupling to electronic states:
T1u
symmetry
vibration
A1g
symmetry
vibration
(symbols have same meaning for
vibrations: A = non-degenerate,
T = triply degenerate, g = gerade,
u = ungerade, etc.)
The band one sees in the
UV-visible spectrum is the
sum of bands due to transitions
to coupled electronic (E) and
vibrational energy levels (υ1, υ2, υ3)
observed
spectrum
E E- υ1
E- υ2
E- υ3
E + υ1’
E + υ2’
E + υ3’
26

27. The spectra of high-spin d5 ions:
6A2g →4T2g
energy
For high-spin d5 ions all possible d-d transitions are spin-forbidden. As a
result, the bands in spectra of high-spin complexes of Mn(II) and Fe(III)
are very weak, and the compounds are nearly colorless. Below is shown
a d-d transition for a high-spin d5 ion, showing that it is spin-forbidden.
eg
eg
t2g t2g
Complexes of Gd(III) are colorless, while those of other lanthanide
M(III) ions are colored, except for La(III) and Lu(III). Why is this? 27

28. Square Planar Complexes
Orbitals and Transitions
28

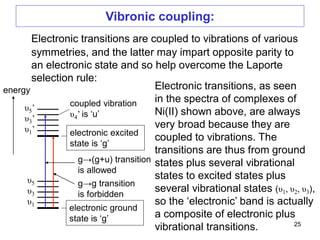
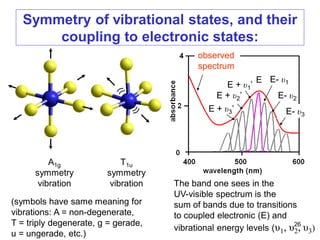
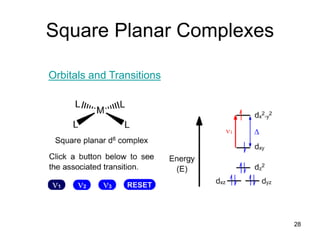
29. The spectra of complexes of tetrahedral
metal ions:
A tetrahedron has no center of symmetry, and so orbitals in
such symmetry cannot be gerade. Hence the d-levels in a
tetrahedral complex are e and t2, with no ‘g’ for gerade.
This largely overcomes the Laporte selection rules, so that
tetrahedral complexes tend to be very intense in color. Thus,
we see that dissolving CoCl2 in water produces a pale pink
solution of [Co(H2O)6]2+, but in alcohol tetrahedral
[CoCl2(CH3CH2OH)2] forms, which is a very intense blue
color. This remarkable difference in the spectra of
octahedral and tetrahedral complexes is seen on the next
slide:
29

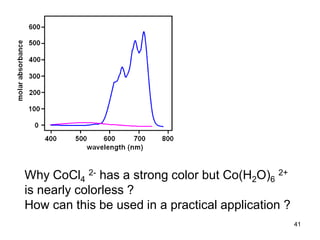
30. The spectra of octahedral [Co(H2O)6]2+ and
tetrahedral [CoCl4]2- ions:
[CoCl4]2-
[Co(H2O)6]2+
The spectra at left
show the very intense
d-d bands in the blue
tetrahedral complex
[CoCl4]2-, as compared
with the much weaker
band in the pink
octahedral complex
[Co(H2O)6]2+. This
difference arises
because the Td com-
plex has no center of
symmetry, helping to
overcome the g→g
Laporte selection rule.
30

31. Tanabe-Sugano Diagrams
31

32. Free ion
terms
Spin allowed
transitions
Example d2
32

33. 33

34. Calculate o
Energy ratio from the
peaks
Find ratio in the
diagram
=> o/B value
From the E/B and
the o/B value:
find B and o
o/B = 30 and E/B = 28
=> o = 30 * B = 30 * E/28 = 30 * 17200/28
 18500 cm-1 34

35. Exercise: Cr3+
Estimate the wavenumbers of the 2 peaks and calculate o
from the Tanabe Sugano diagram
35

36. Tanabe Sugano for d3
Estimate /B and E/B from
the Energy-relation of the 2
peaks in the spectrum.
From there you can calculate
the parameter B and from
there the splitting energy o
36

37. 37
(1) Ratio of peak energies: 31000/ 23000 = 1.4

38. 38
(2) Find the ratio 1.4 in the diagram
The ratio 1.4 can be found for a
line at /B = 24
=> E/B = 34 and 24
 B = E(1)/24 = 23000/24 = 960
  = B * 24 = 23000 cm-1

39. 39
Questions
Which electronic state is ground and excited state and what is the
name ?
Which transition is stronger and why ?

40. 40
Why there are 2 different 3T2 excited state ?
Why are high-spin d5 complexes colorless ?

41. 41
Why CoCl4
2- has a strong color but Co(H2O)6
2+
is nearly colorless ?
How can this be used in a practical application ?

42. End of UV/VIS Part 1
42