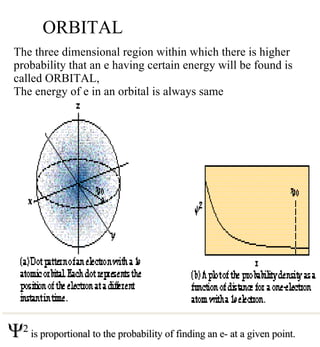
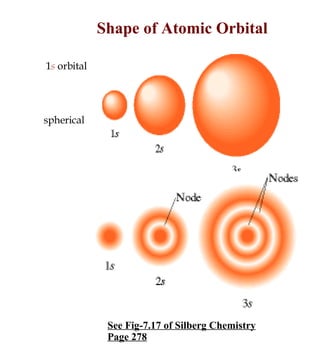
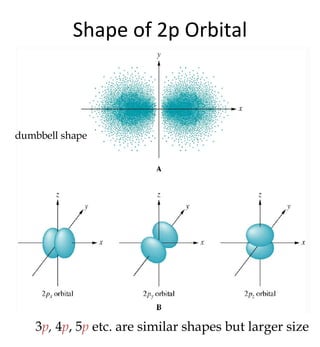
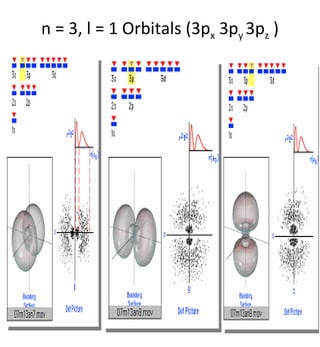
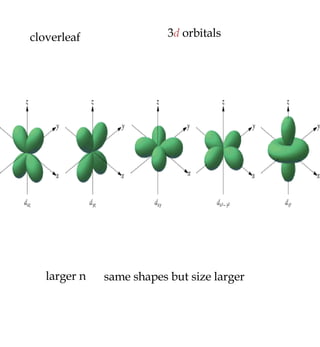
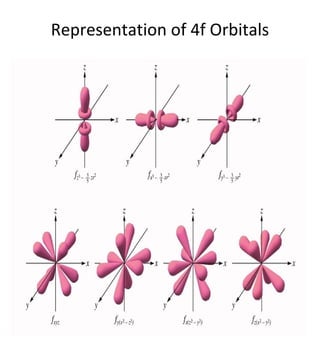
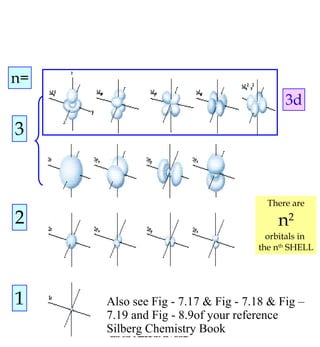
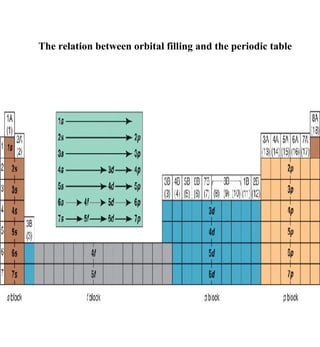
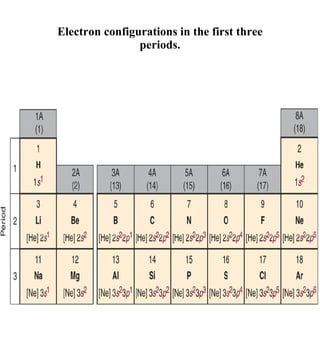
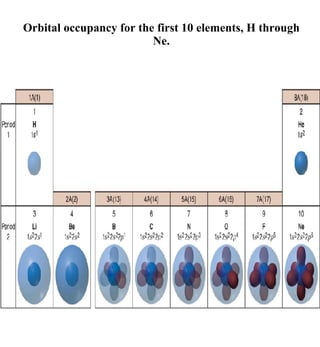
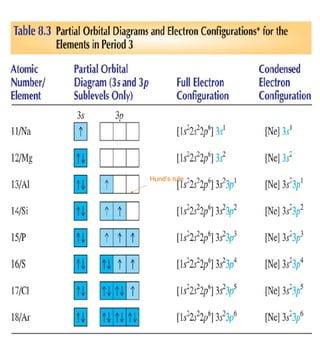
1) The document discusses the electronic configuration of atoms, including the development of wave mechanics and quantum theory to explain the structure of atoms. It introduces concepts like the de Broglie wavelength, quantum numbers, atomic orbitals and shapes, Pauli's exclusion principle, and Hund's rule for electron configuration. 2) Key scientists discussed include de Broglie, Heisenberg, Schrodinger, Pauli, and their contributions to developing models of the atom and allowing prediction of electron configurations. 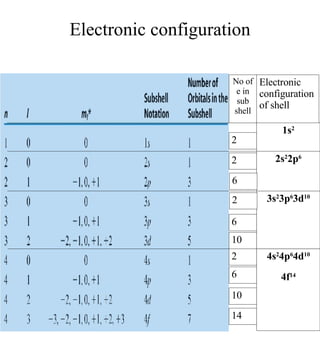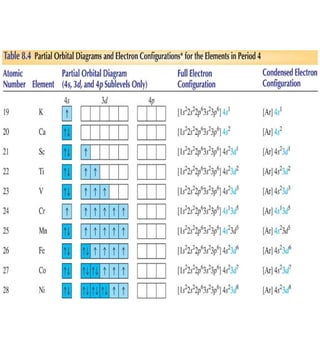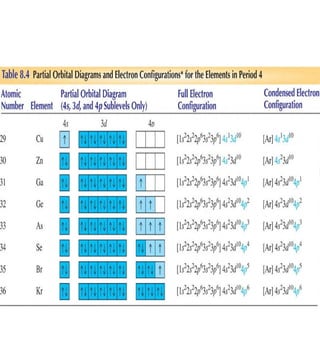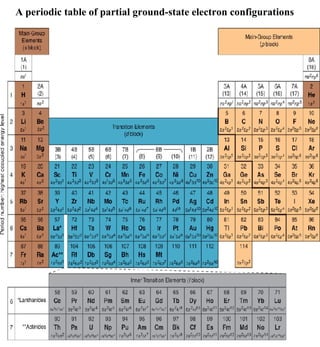3) The document provides examples of writing out electron configurations for elements and explaining the rules for filling atomic orbitals in the Aufbau principle.

1. Electronic configuration of Atom Lecture 7 Week 4

2. Wave Mechanics In 1924, de Broglie proposed that if energy is particle like, perhaps matter is wavelike According to his theory, e - , p + and even atom, when in motion possessed wave properties and could be associated with λ , ν and А = this is WAVE MECHANICS For light: E = h  = hc /  For particles: E = mc 2 (Einstein) L. de Broglie (1892-1987)  for particles is called the de Broglie wavelength  From previous lecture we know that, Light as well as heat energy exhibits both wave and particle nature under suitable conditions = Wave mechanical theory Therefore, mc = h /  and for particles (mass)x(velocity) = h / 

3. If particle travel in waves, e should exhibit diffraction & interference - in 1927, Davisson & Germer guided a beam of electrons at nickel crystal and obtain a diffraction pattern. Ex: see Fig. 7.14 of page 271 of your reference Silberg Chemistry book Do a math: a) a stone of mass 100gm moving with a velocity 10m/s. What is the de Broglie’s λ for the stone? b) an e in H atom has a mass 9.1091×10 -28 gm and moves with a velocity 2.188×10 -8 cm/s. what is the de Broglie’s λ ? Wave length of X-rays is 1nm = 1×10 -9 m. Compare X-rays λ with de Broglie’s λ .

4. Uncertainty Principle If an e has the properties of both a particle and a wave, so we should be able to determine the location of e in the atom. In 1927, W. Heisenberg postulated, The Uncertainty principle, which states that it is impossible to know simultaneously the exact position and momentum (velocity) of a particle/ electron . Heisenberg’s relationship is: Δ x. m Δ u ≥ h/2 π This uncertainty product is negligible in case of large objects It means that we can not assign fixed path for e, such as circular orbits of Bohr’s model At best we can do is find the probability of finding an e with a probable velocity. W. Heisenberg 1901-1976 So, in macroscopic world, a moving particle has a definite location at any instant and a wave is spread out in space.

5. Using this idea, Schrodinger developed a mathematical model based on wave mathematics to describe the position of e in an atom=calculation of the probability of finding e at various points at atom. For a given atom, Schrodinger's Equation has many solutions, and each solution is associated with a given wave functions, Ψ , a mathematical description of electron’s motion, also called Atomic Orbital . E. Schrodinger 1887-1961 Ψ does NOT describe the exact location of the electron, but Ψ 2 is proportional to the probability of finding an e- at a given point

6. ORBITAL  2 is proportional to the probability of finding an e- at a given point. The three dimensional region within which there is higher probability that an e having certain energy will be found is called ORBITAL, The energy of e in an orbital is always same

7. By examining the probabilities given by a particular orbital, a "shape" of the orbital can be seen. This shape represents a space around the nucleus that the electron is most likely to be found. The many solutions to Schrodinger's equation can be classified by the shape that is from their probability distributions, called orbital, like s , p , and d-type , as shown above. Most orbital types have several possible orientations too. An atomic orbital is specified by three quantum numbers . One is related to orbital’s size, another its shape third its orientation in space Quantum number of an atomic Orbital

8. Those are principal ( n ) , angular ( l ) , and magnetic ( m ) quantum numbers n l m principal 1, 2, 3, … size and energy angular momentum 0, 1, 2, …, ( n - 1) shape magnetic - l , …, l orientation

9. Quantum number of an atomic Orbital Those are the principal ( n ) , angular momentum( l ) , and magnetic ( m ) quantum numbers. The principle quantum number (n): It actually denotes the principal shell/energy level to which electrons belongs at the atom. It represents the avg. size of atom. Incase of H atom it represents the only orbital of it . n is a positive integer (1,2,3,…….7) In n’th energy level, atom can have only 2n 2 number of electrons Principal quantum number (n) 1 2 3 4 Max. number of electrons in n’th shell/level 2 8 18 32

10. n = 1 l = 0 = (1s) n = 2 l = 0, 1 = (2s, 2p) n = 3 l = 0, 1, 2 = (3s, 3p, 3d) n = 4 l = 0, 1, 2, 3 = (4s, 4p, 4d, 4f) designated by letters l = 0 s orbital l = 1 p orbital l = 2 d orbital l = 3 f orbital Angular momentum quantum number ( l ) It is an integer from 0 to (n-1) It is related to the shape of the orbital

11. n = 1 l = 0 m = 0 n = 2 l = 0 m = 0 l = 1 m = -1 m = 0 m = 1 n = 3 l = 0 m = 0 l = 2 l = 1 m = -1 m = 0 m = 1 m = -2 m = -1 m = 0 m = 1 m = 2 s s p s p d 1 1 3 3 1 5 Magnetic quantum number ( l ) It is an integer from –l through 0 to +l It is prescribes the orientation of the orbital in space around nucleus

12. For, n = 1 , l = 0 and m = 0 There is only one subshell and that subshell has a single orbital (m has a single value ---> 1 orbital) This subshell is labeled s and we call this orbital 1s Each shell has 1 orbital labeled s. It is SPHERICAL in shape. An atomic orbital is defined by 3 quantum numbers: n l m Electrons are arranged in shells and subshells of ORBITALS . n  shell l  subshell m  designates an orbital within a subshell Shells and Subshells

13. p Orbital & d Orbital For n = 3, what are the values of l? l = 0, 1, 2 and so there are 3 subshells in the shell. For l = 0, m l = 0  s subshell with single orbital For l = 1, m l = -1, 0, +1  p subshell with 3 orbitals For l = 2, m l = -2, -1, 0, +1, +2  d subshell with 5 orbitals For, n = 2, l = 0 and 1 There are 2 types of orbitals — 2 subshells For l = 0 m l = 0 this is a s subshell For l = 1 m l = -1, 0, +1 this is a p subshell with 3 orbitals

14. 1 s orbital spherical Shape of Atomic Orbital See Fig-7.17 of Silberg Chemistry Page 278

15. Shape of 2p Orbital dumbbell shape 3 p , 4 p , 5 p etc. are similar shapes but larger size

16. n = 3, l = 1 Orbitals (3p x 3p y 3p z )

17. 3 d orbitals cloverleaf larger n same shapes but size larger

18. Representation of 4f Orbitals

19. There are n 2 orbitals in the n th SHELL Also see Fig - 7.17 & Fig - 7.18 & Fig – 7.19 and Fig - 8.9of your reference Silberg Chemistry Book 2 1 3d n= 3

20. Spin Quantum Number ( s ) The spin quantum value indicates that the electron is spinning on its axis in one direction (clockwise/anti clockwise) or the opposite. It can have a value of -1/2 or +1/2 only The value of s does not depend on any other quantum number These spins are also designated by arrows pointing upwards and downwards as

21. Do this math Which of the following sets of quantum numbers are not allowable and why? a) n= 2, l=2, m=0, s=+1/2 b) n=2, l=0, m=-2, s=-1/2 c) n=3, l=2, m=+2, s=-1/2 What designation are given to the following orbital? a) n=4, l=3 b) n=5, l=0 c) n=2, l=1 Write the missing quantum numbers & sublevel names n l m name a) ? ? 0 4p b) 2 1 0 ? c) 3 2 -2 ? d) ? ? ? 2s

22. Pauli’s exclusion principle In 1925, Wolfgang Pauli discover the principle that governs the arrangements of electrons in many electron atoms The Pauli exclusion principle states that no two electrons in an atom can have the same set of four quantum numbers n, l, m, s. For a given orbital, thus e value of n, l,m are fixed Thus if we want to put more than one e in an orbital and satisfy the Pauli exclusion principle, our only option is to assign different values of s to those two e We know that their can be only two s value possible for e We conclude that, an orbital can hold a max. of two e, and they must have opposite spin.

23. Example of Pauli’s Exclusion Principal: Consider the second shell (n=2) There are 4 orbitals, one s orbital (l=0) and three p orbitals (l=1) 2 e are in 2s orbital 2 e are in 2p x orbital 2 e are in 2p y orbital 2 e are in 2p z orbital n l m s 2 0 0 +1/2 2 0 0 -1/2 2 1 +1 +1/2 2 1 +1 -1/2 2 1 -1 +1/2 2 1 -1 -1/2 2 1 0 +1/2 2 1 0 -1/2

24. Electronic configuration No of e in sub shell Electronic configuration of shell 1s 2 2s 2 2p 6 3s 2 3p 6 3d 10 4s 2 4p 6 4d 10 4f 14 2 10 6 14 10 2 2 6 6 2

25. Rules of electronic configuration of atom Each e shell can hold max. 2n 2 electrons Pattern of e entering in shell: 1 2 3 4 5 6 7 Pattern of e entering in subshell: s p d f Entering of e in orbital/ Hund’s rule: Electrons are distributed among the orbitals of a subshell in such a way as to give the max. number of unpaired e and have the same direction of pair

26. Aufbau or Building up rule Electrons tend to occupy the available orbitals in increasing order of energies, the orbital of lower energy being filled first. This is building up/Aufbau principle The energy of an orbital is determined by the sum of principle quantum number (n) & the angular quantum number (l), this is (n+l) rule If in case of two orbital having the same (n+l) value, the orbital with with lower value of n has lower energy. Rules of electronic configuration of atom (n+l) rule

27. The relation between orbital filling and the periodic table

28. Write electron configuration of the following elements O (8) = ? K (19) = ? Cl (17) = ? Fe (26) = ? Zn (30) = ? Pb (82) = ?

29. Electron configurations in the first three periods.

30. Orbital occupancy for the first 10 elements, H through Ne.

31. Hund’s rule

34. A periodic table of partial ground-state electron configurations

35. Assignment 1 Questions number 5, 9, 12, 16 & 23 to 33 . Among these 14 questions answer any 7 questions Clearly write your name & ID no in the front cover of your assignment sheet You can submit the assignment in hand written or as printed form, as you like Last date of submission of Assignment 1 is November 15, 2008. If anyone submit the Assignment 1 before November 8, 2008 then he/she will be given Bonus 2 marks at the final If anyone answers all 14 questions correctly and submit his/her Assignment copy then he/she will be rewarded with Bonus 5 marks at the final Suggestion : Please prepare your notes at least according to the question banks, you can show me your notes, if any correction needed or suggestion then I can give you that.