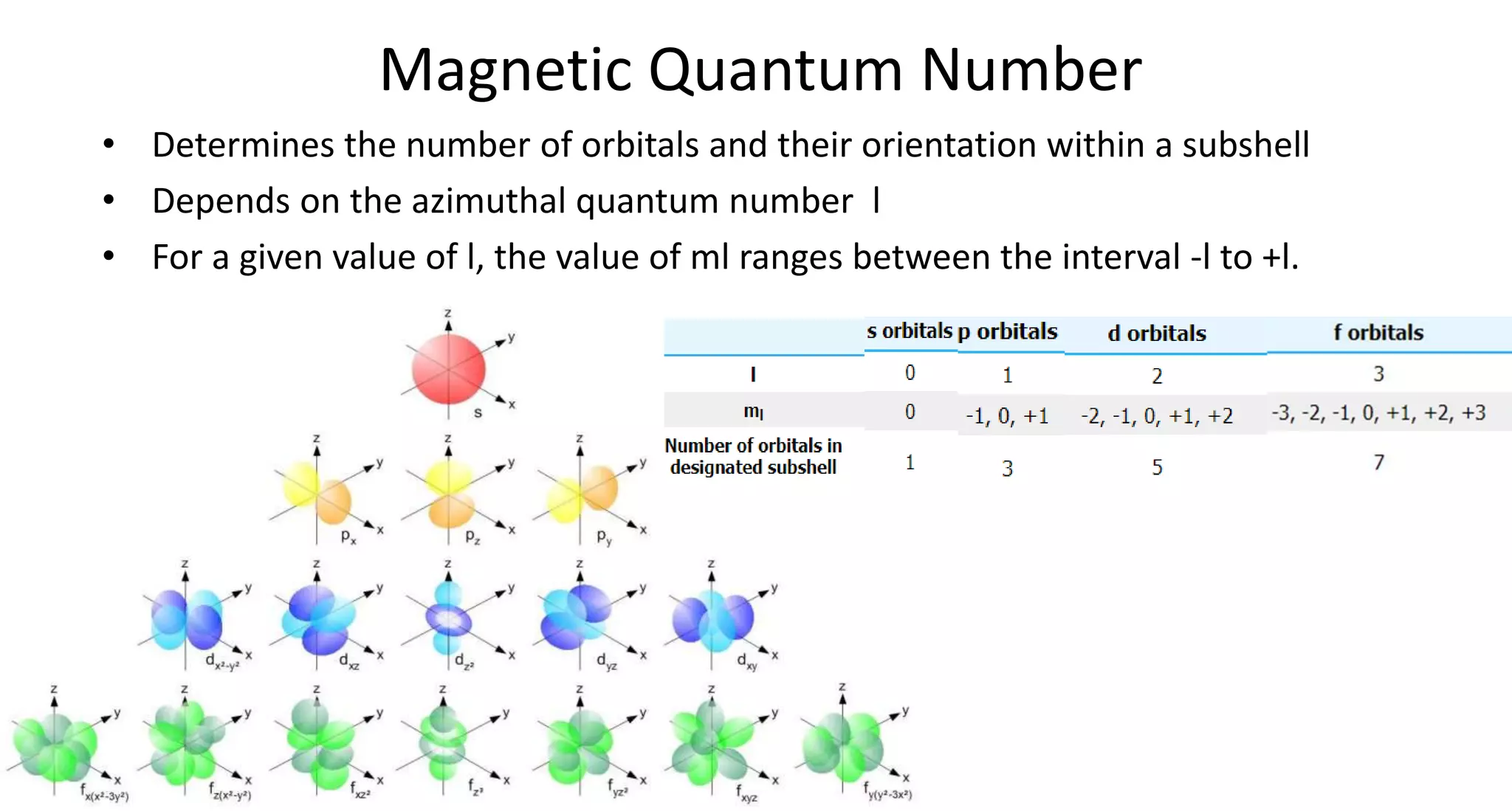
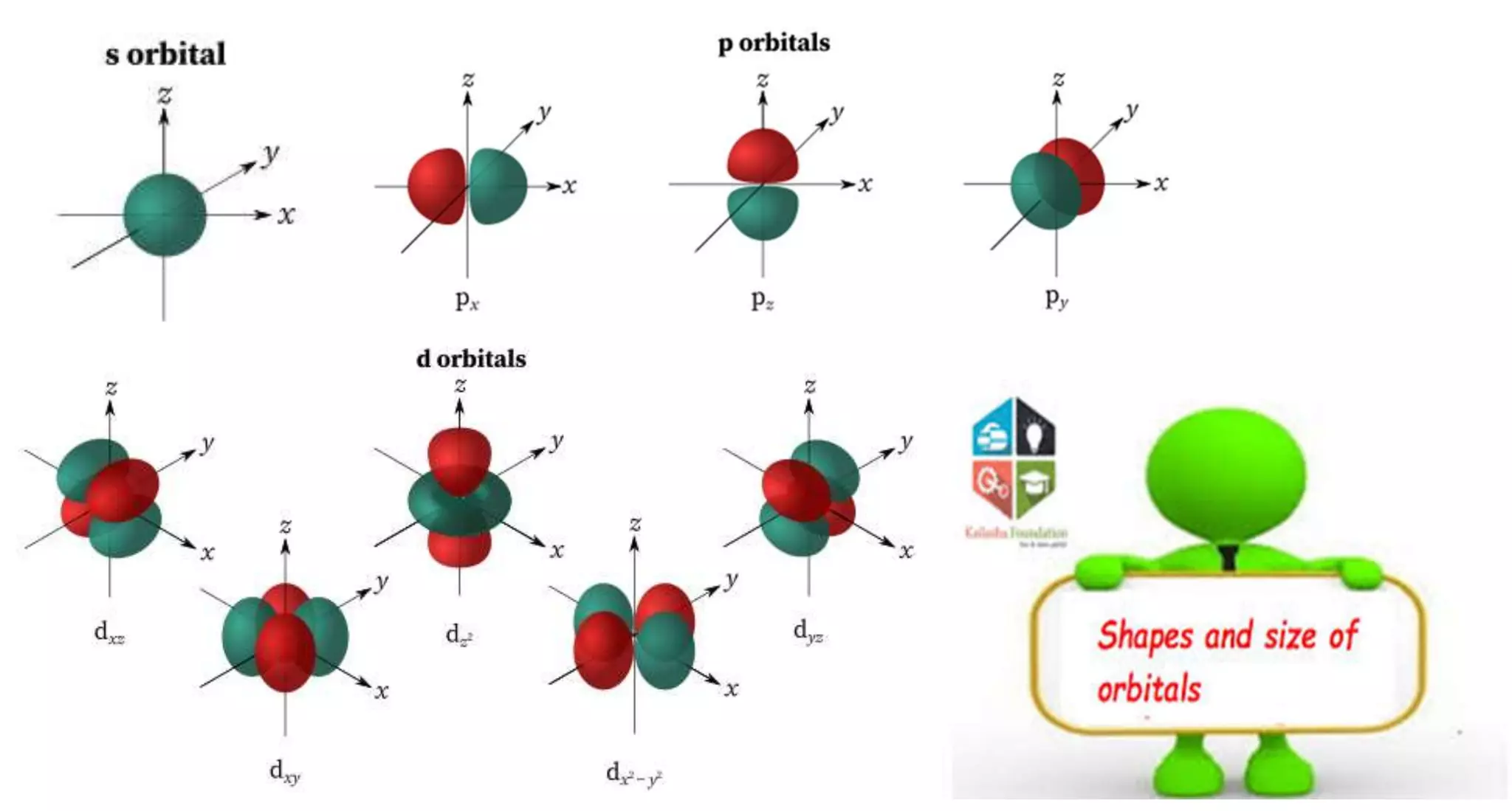
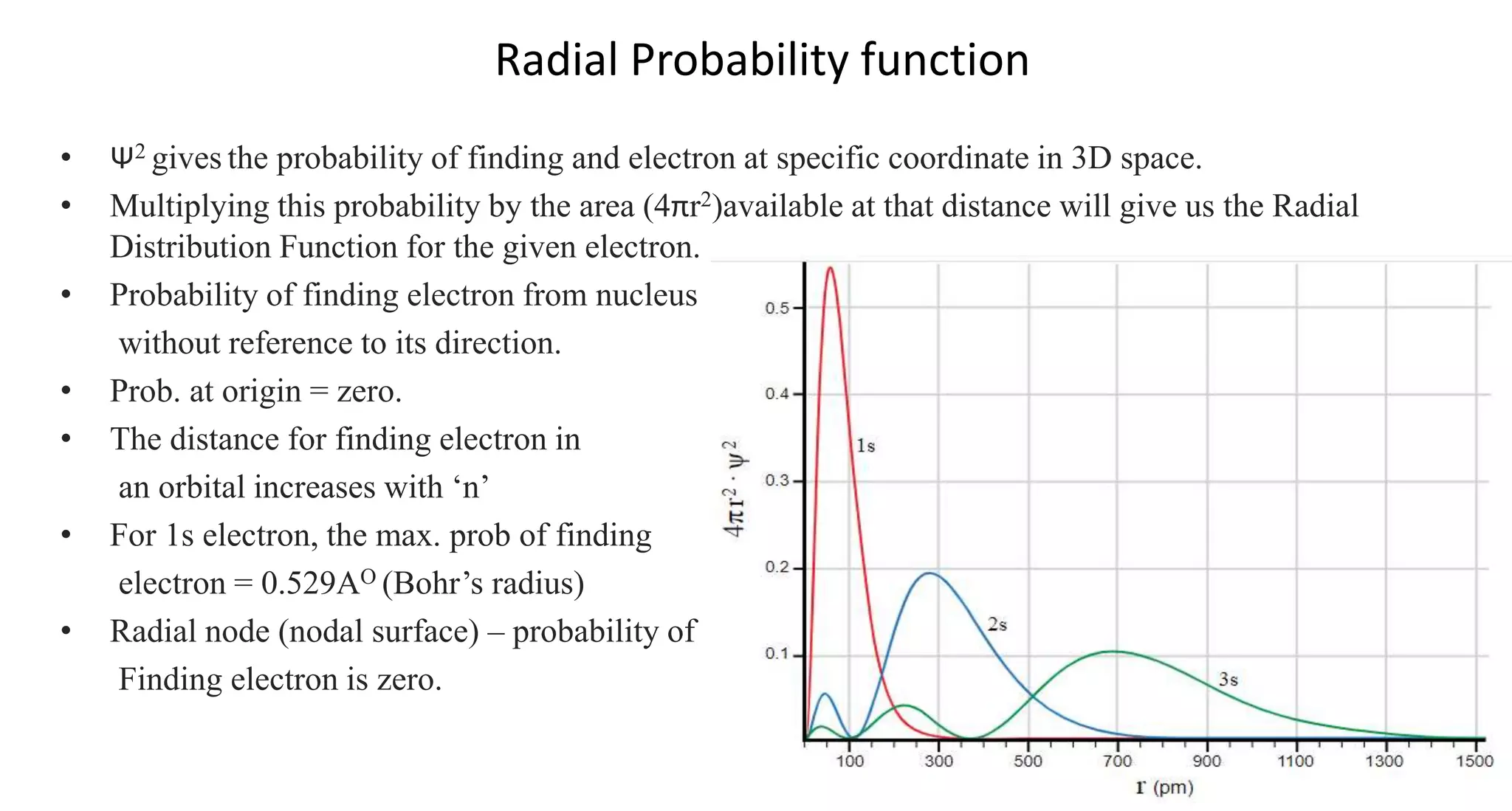
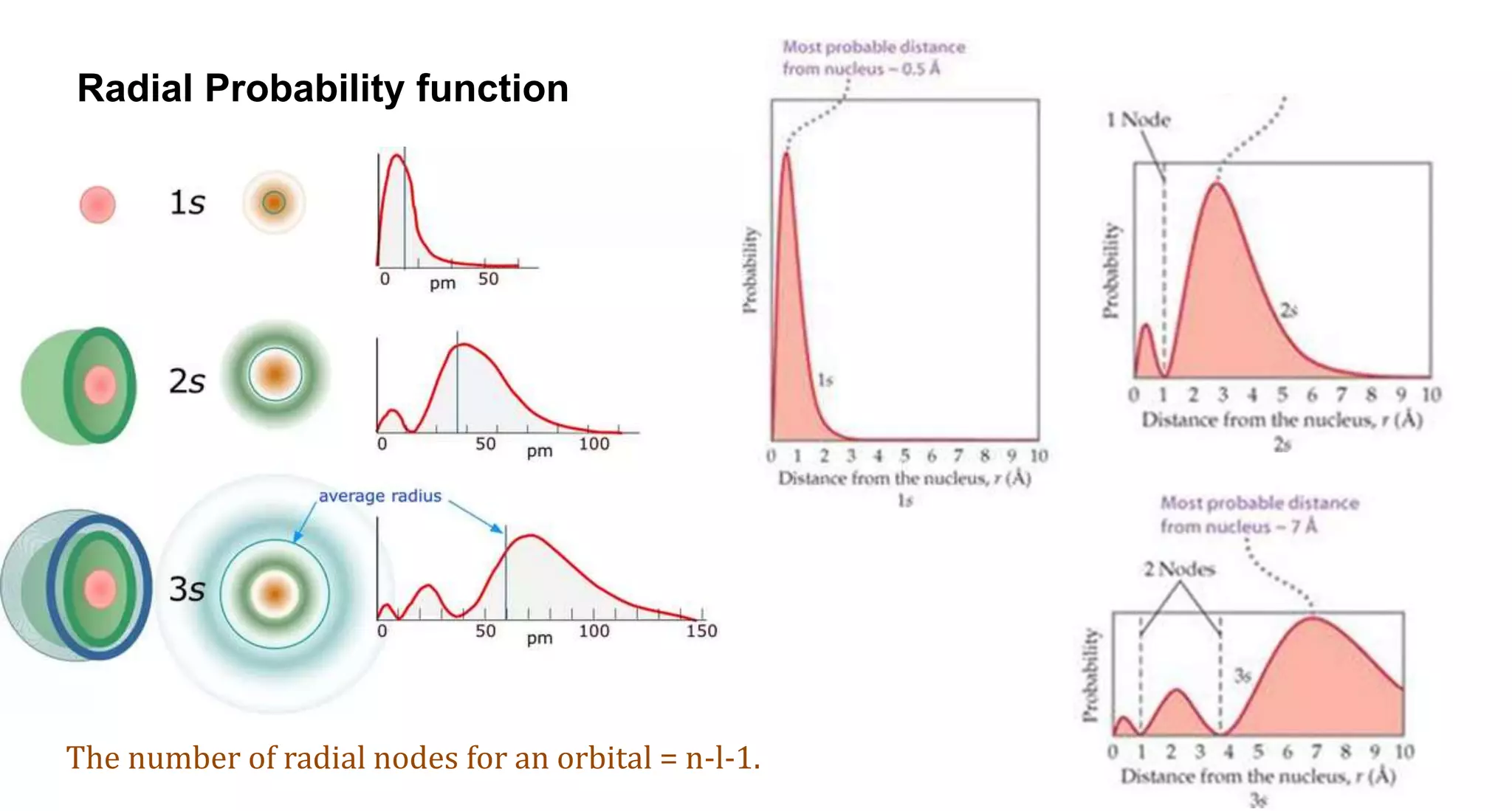
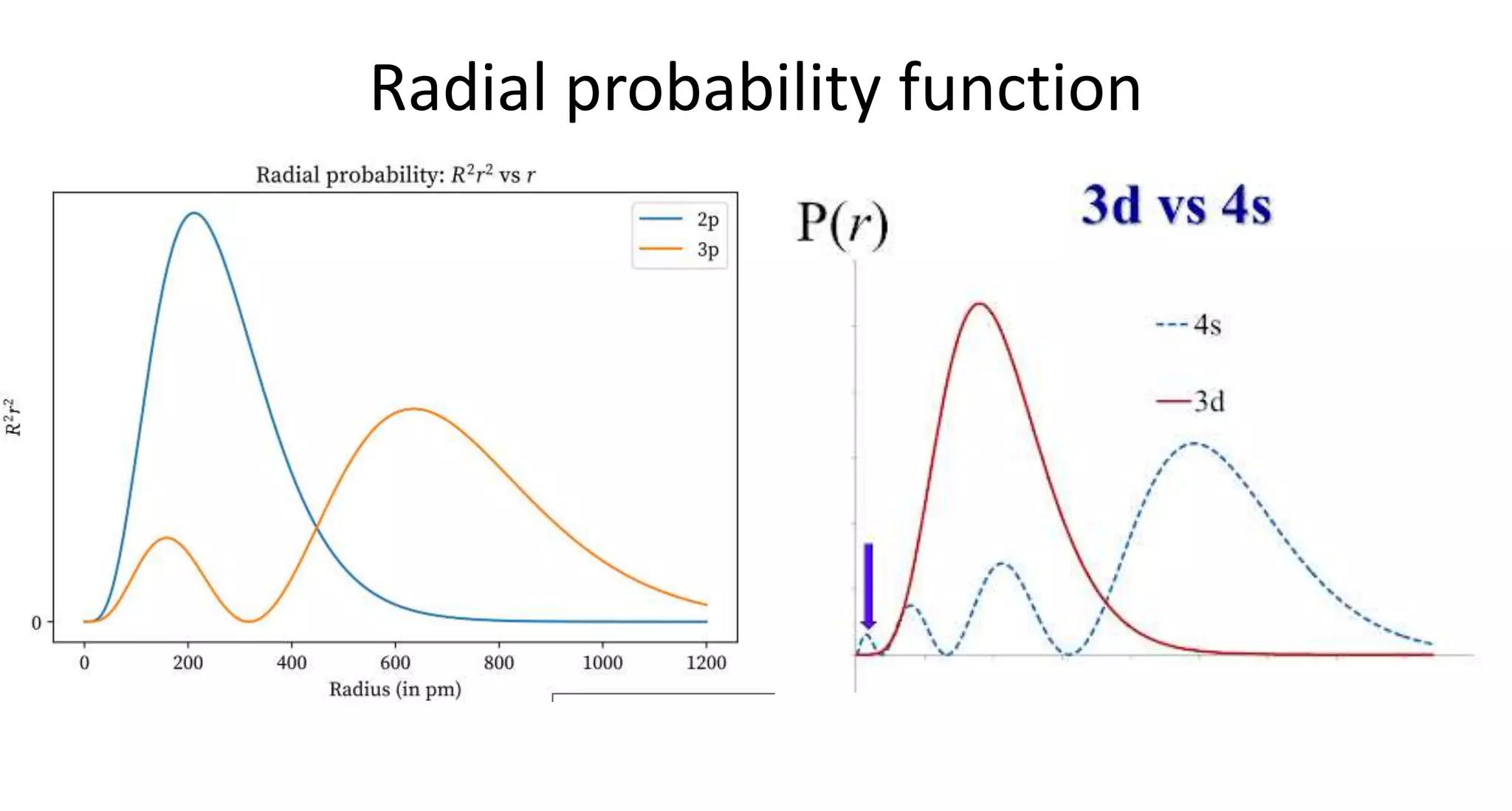
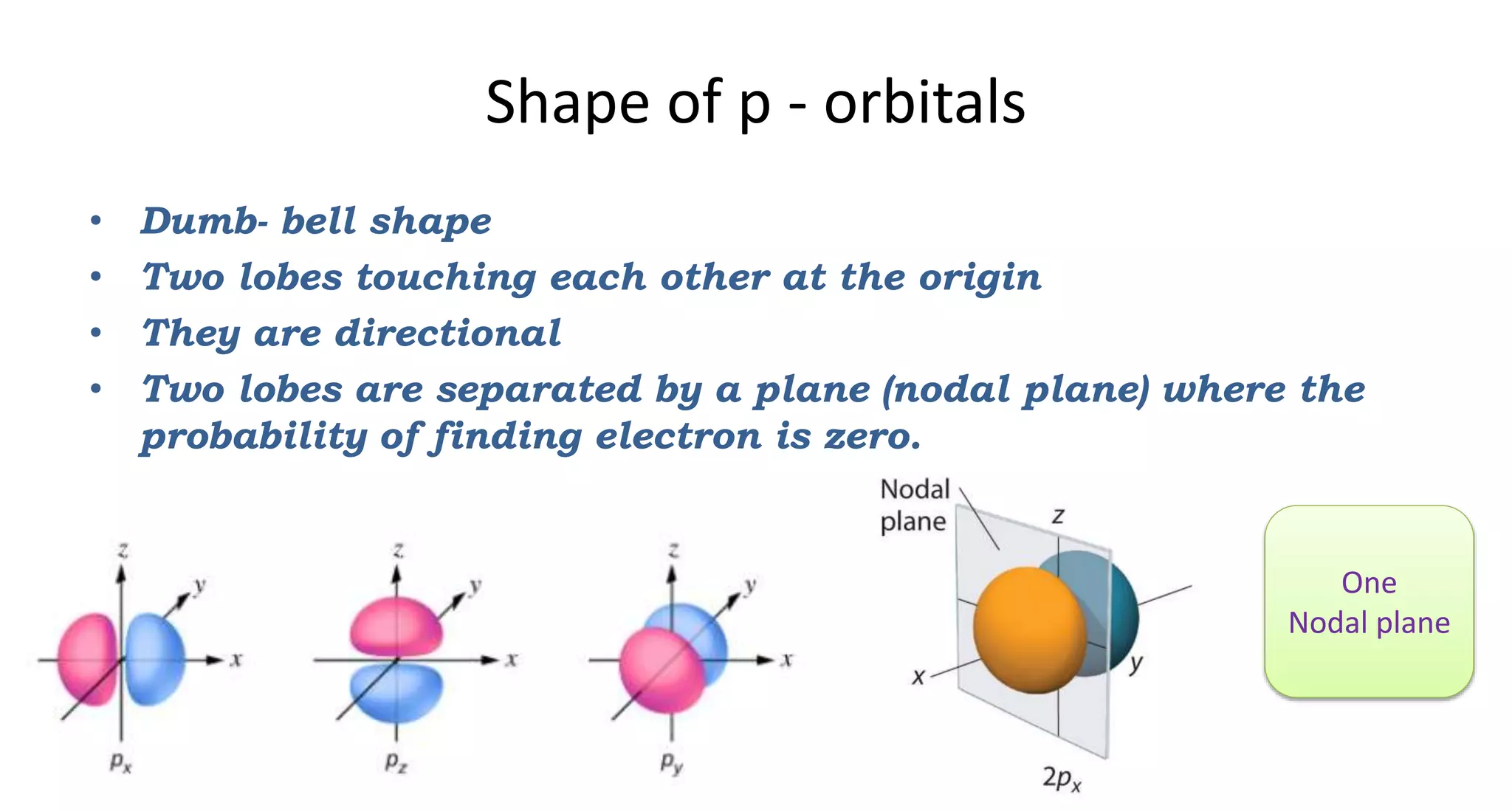
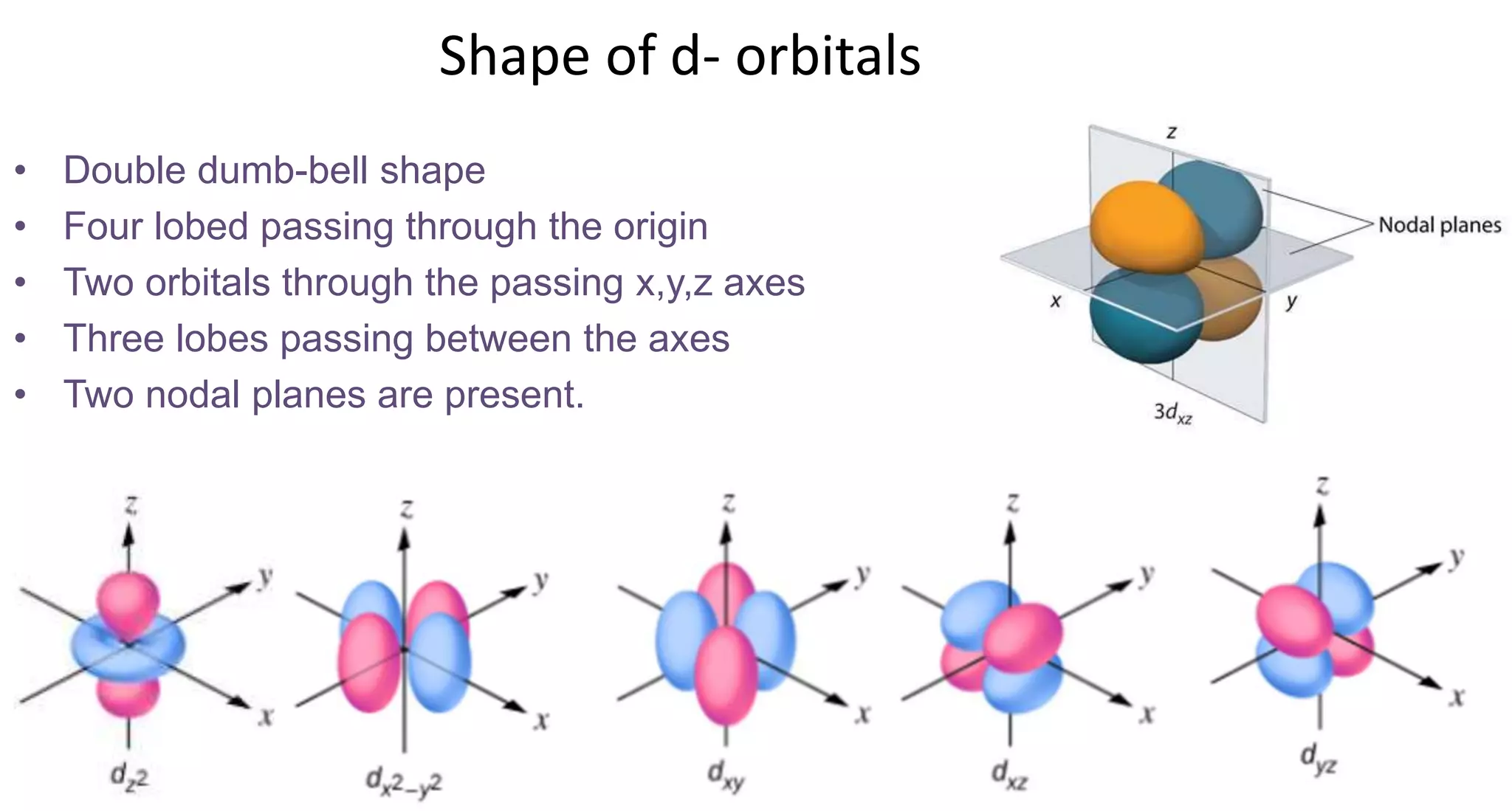
This document discusses quantum numbers and probability distribution curves. It introduces the four quantum numbers - principal, azimuthal, magnetic, and spin - that are used to determine the energy of electrons in atoms. It describes each quantum number and what properties they indicate, such as the electron shell or subshell, orbital shape, and electron spin. It then discusses radial and angular probability functions, which describe the probability of finding an electron at different distances from the nucleus or at different angles, helping to determine the shape and number of lobes in an orbital.

1. Quantum numbers & Probability
distribution curves

2. Quantum numbers
• The mathematical solution of Schrodinger’s equation introduced four numbers that
were called quantum numbers , to determine the energy of an electron in multi-
electron atoms
• Used to describe completely the movement and trajectories of each electron within an
atom.
• Principal Quantum Number (n)
• Azimuthal Quantum number (l)
• Magnetic Quantum number (m)
• Spin Quantum number (s)

3. Principal Quantum Number
• describes the electron shell, or energy level, of an atom.
• describes tells the most probable distance of the electrons from the nucleus
• has whole number values 1 , 2 , 3 , 4 , ……. etc
• Also be designated as K,L,M,N, …… etc
• larger the number n , the larger the size of the orbit
• The maximum number of electrons in n is 2n2
• Also called as orbit.

4. Azimuthal Quantum Number
• Describes the shape of a given orbital.
• Each value of l indicates a specific subshell
• Subshell has whole number value starting from 0,1,2,3,4,……….
• The value of ℓ ranges from 0 to n − 1
• The maximum number of electrons in ℓ is 4ℓ +2
• Symbols of sub-levels , s = 0 , p = 1 , d = 2 , f = 3
• denotes the angular momentum and is given by the formula

5. Magnetic Quantum Number
• Determines the number of orbitals and their orientation within a subshell
• Depends on the azimuthal quantum number l
• For a given value of l, the value of ml ranges between the interval -l to +l.

7. Spin Quantum Number
• independent of the values of n, l, and m
• gives insight into the direction in which the electron is spinning
• The possible values are +½ and -½.
• Helps in the determination of an atom's ability to
generate a magnetic field or not.

8. Summary

9. Radial Probability function
• Ψ2 gives the probability of finding and electron at specific coordinate in 3D space.
• Multiplying this probability by the area (4πr2)available at that distance will give us the Radial
Distribution Function for the given electron.
• Probability of finding electron from nucleus
without reference to its direction.
• Prob. at origin = zero.
• The distance for finding electron in
an orbital increases with ‘n’
• For 1s electron, the max. prob of finding
electron = 0.529AO (Bohr’s radius)
• Radial node (nodal surface) – probability of
Finding electron is zero.

10. Radial Probability function
The number of radial nodes for an orbital = n-l-1.

11. Radial probability function

12. Angular probability function
• The square of the angular distribution function describes the probability of
finding the electron at angles θ and φ.
• The Angular distribution function describes the basic shape of the orbital, or the
number of lobes in an orbital.
• The angular distribution functions depend only on the quantum number l.
Total no. of angular nodes for any orbital = l
S – orbital is independent
of θ and φ.
Spherical

13. Shape of p - orbitals
• Dumb- bell shape
• Two lobes touching each other at the origin
• They are directional
• Two lobes are separated by a plane (nodal plane) where the
probability of finding electron is zero.
One
Nodal plane

14. Shape of d- orbitals
• Double dumb-bell shape
• Four lobed passing through the origin
• Two orbitals through the passing x,y,z axes
• Three lobes passing between the axes
• Two nodal planes are present.