1) Molecular term symbols employ symmetry labels from group theory to mark the electronic energy levels of diatomic molecules similarly to atomic term symbols under the Russell-Saunders coupling scheme.
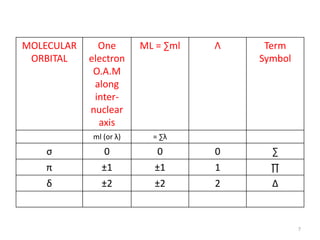
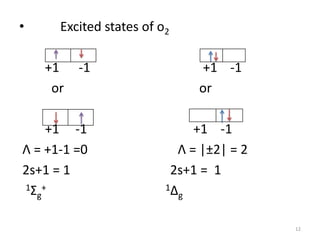
2) Heteronuclear diatomic molecules have C∞v symmetries and homonuclear ones have D∞h symmetries, with their irreducible representations symbolized using notations like Σ, Π, Δ. Term symbols include quantum numbers like Λ (orbital angular momentum), Ω (total angular momentum), and S (spin multiplicity).
3) Selection rules for electronic transitions between terms include ΔΛ = 0, ±1; ΔS = 0; and ΔΩ = 0, ±