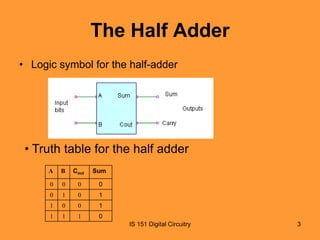
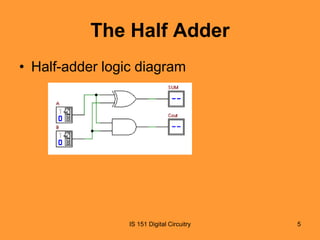
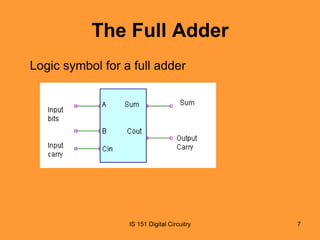
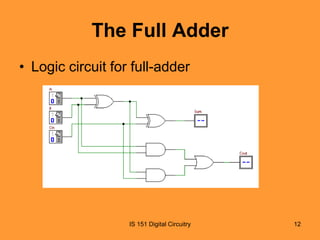
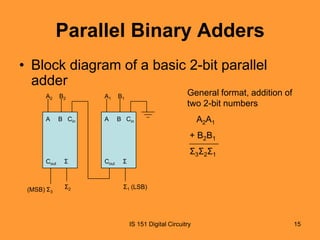
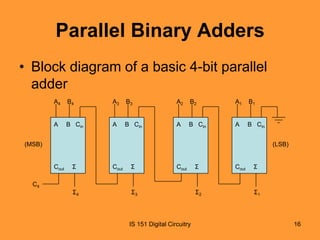
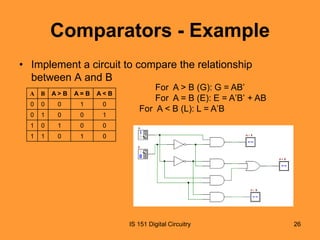
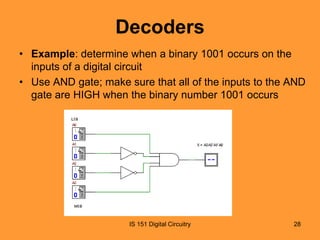
This document discusses basic combinational logic functions including adders, comparators, decoders, and encoders. It begins by explaining half adders and full adders, including their truth tables and logic expressions. It then covers parallel binary adders used to add multi-bit numbers. Comparators are introduced for comparing the magnitude of two binary quantities. Decoders and encoders are also discussed, with decoders detecting a specified input code and encoders performing the reverse by converting an input to a coded output. Examples and exercises are provided to illustrate the concepts.

1. Functions of Combinational
Logic
• Basic Adders
– Important in computers and many types of
digital systems to process numerical data
– Basic adder operations are fundamental to
the study of digital systems
IS 151 Digital Circuitry
1

2. The Half Adder
• Basic rules of binary addition
–0+0=0
–0+1=1
–1+0=1
– 1 + 1 = 10
• A half-adder accepts 2 binary digits on its
inputs and produces two binary digits on
its outputs – a sum bit and a carry bit
IS 151 Digital Circuitry
2

3. The Half Adder
• Logic symbol for the half-adder
• Truth table for the half adder
A
B
Cout
Sum
0
0
0
0
0
1
0
1
1
0
0
1
1
1
1
0
IS 151 Digital Circuitry
3

4. The Half Adder
• Derive expressions for the Sum and Cout
as functions of inputs A and B
• From the truth table:
– Cout is a 1 only when both A and B are 1s:
Cout = AB
– Sum is a 1 only if A and B are not equal:
Sum = A B
IS 151 Digital Circuitry
4

5. The Half Adder
• Half-adder logic diagram
IS 151 Digital Circuitry
5

6. The Full Adder
• Accepts 3 inputs including an input carry
and generates a sum output and an
output carry
• Difference between half and full-adder
– the full adder has three inputs (including an
input carry) while a half adder has only two
inputs (without the input carry)
IS 151 Digital Circuitry
6

7. The Full Adder
Logic symbol for a full adder
IS 151 Digital Circuitry
7

8. The Full Adder
• Full adder truth table
A
B
Cin
Cout
Sum
0
0
0
0
0
0
0
1
0
1
0
1
0
0
1
0
1
1
1
0
1
0
0
0
1
1
0
1
1
0
1
1
0
1
0
1
1
1
1
1
IS 151 Digital Circuitry
8

9. The Full Adder
• Derive expressions for the Sum and Cout
as functions of inputs A, B and Cin from the
truth table
• Alternatively, using knowledge from the
half adder:
– Sum = inputs exclusively-ORed
• Sum = (A
B) Cin
– Cout = inputs ANDed
• AB + (A B)Cin
IS 151 Digital Circuitry
9

10. The Full Adder
• From the truth table:
– Sum = A’B’C + A’BC’+ AB’C’ + ABC
–
= A’B’C + ABC + A’BC’ + AB’C’
–
= C(A’B’ + AB) + C’(A’B + AB’)
–
= C(AexB)’ + C’(AexB)
–
= CexAexB
–
= AexBexC
IS 151 Digital Circuitry
10

11. The Full Adder
• Also from the truth table:
– Carry out = A’BC + AB’C ABC’ + ABC
–
= C(A’B + AB’) + AB(C’ + C)
–
= C(AexB) + AB
–
= AB + (AexB)C
IS 151 Digital Circuitry
11

12. The Full Adder
• Logic circuit for full-adder
IS 151 Digital Circuitry
12

13. The Full Adder - Exercise
• Determine an alternative method for
implementing the full-adder
– Write SoP expressions from the truth table for
Sum and Cout
– Map the expressions on K-maps and write
simplified expressions if any
– Implement/draw the circuit diagram for the
full-adder
IS 151 Digital Circuitry
13

14. Parallel Binary Adders
• A single full adder is capable of adding two 1- bit
numbers and an input carry
• To add binary numbers with more than one bit,
additional full-adders must be used.
• Example, for a 2-bit number, 2 full adders are
used, 4-bit numbers, 4 full-adders are used, etc.
• The carry output of each adder is connected to
the carry input of the next higher-order adder
IS 151 Digital Circuitry
14

15. Parallel Binary Adders
• Block diagram of a basic 2-bit parallel
adder
General format, addition of
two 2-bit numbers
A2
B2
A1
B1
A
B Cin
A
B Cin
A2A1
+ B2B1
Σ3Σ2Σ1
Cout
(MSB) Σ3
Σ
Σ2
Cout
Σ
Σ1 (LSB)
IS 151 Digital Circuitry
15

16. Parallel Binary Adders
• Block diagram of a basic 4-bit parallel
adder
A4
B4
A3
B3
A2
B2
A1
B1
A
B Cin
A
B Cin
A
B Cin
A
B Cin
(MSB)
(LSB)
Cout
Σ
Cout
Σ
Cout
Σ
Cout
Σ
C4
Σ4
Σ3
IS 151 Digital Circuitry
Σ2
Σ1
16

17. Comparators
• Basic function – to compare the magnitudes
of two binary quantities to determine the
relationship of those quantities
• Comparators determine whether two
numbers are equal or not
IS 151 Digital Circuitry
17

18. Comparators
• Basic comparator operations
The input bits are equal
The input bits are not equal
The input bits are equal
IS 151 Digital Circuitry
18

19. Comparators
• To compare binary numbers containing 2
bits each, an additional Ex-OR gate is
required
IS 151 Digital Circuitry
19

20. Comparators
• The two LSBs of the two numbers are compared
by gate G1, and the MSBs are compared by gate
G2
– Binary number A = A1A0
– Binary number B = B1B0
• If the two numbers are equal, their
corresponding bits are the same, and the output
of each Ex-OR gate is a 0
• The 0s are inverted using the inverter, producing
1s
• The 1s are ANDed, producing a 1, which
indicates equality
IS 151 Digital Circuitry
20

21. Comparators
• If the corresponding sets of bits are not equal,
i.e. A0≠B0, or A1≠B1, a 1 occurs on that Ex-OR
gate output (G1 or G2)
• In order to produce a single output indicating an
equality or inequality of two numbers, two
inverters and an AND gate are used
• When the two inputs are not equal, a 1,0 or 0,1
appears on the inputs of the AND gate,
producing a 0, indicating inequality
IS 151 Digital Circuitry
21

22. Comparators - Examples
• Determine whether A and B are equal (or
not) by following the logic levels through
the circuit
– a) A0 = 1, B0 = 0 and A1 = 1, B1 = 0
– b) A0 = 1, B0 = 1 and A1 = 1, B1 = 0
IS 151 Digital Circuitry
22

23. 4-bit Comparators
• To determine if two numbers are equal
• If not, determine which one is greater or
less than the other
• Numbers
– A = A3A2A1A0
– B = B3B2B1B0
IS 151 Digital Circuitry
23

24. 4-bit Comparators
• Determine the inequality by examining
highest-order bit in each other
– If A3 = 1 and B3 = 0; A > B
– If A3 = 0 and B3 = 1; A < B
– If A3 = B3, examine the next lower bit position
for an inequality (i.e. A2 with B2)
IS 151 Digital Circuitry
24

25. 4-bit Comparators
• The three observations are valid for each
bit position in the numbers
• Check for an inequality in a bit position,
starting with the highest order bits
• When such an inequality is found, the
relationship of the two numbers is
established, and any other inequalities in
lower-order bit positions are ignored
IS 151 Digital Circuitry
25

26. Comparators - Example
• Implement a circuit to compare the relationship
between A and B
A
B
A>B
A=B
A<B
0
0
0
1
0
0
1
0
0
1
1
0
1
0
0
1
1
0
1
For A > B (G): G = AB’
For A = B (E): E = A’B’ + AB
For A < B (L): L = A’B
0
IS 151 Digital Circuitry
26

27. Decoders
• Function – to detect the presence of a
specified combination of bits (code) on
inputs and to indicate the presence of that
code by a specified output level
• n-input lines (to handle n bits)
• 1 to 2n output lines to indicate the
presence of 1 or more n-bit combinations
IS 151 Digital Circuitry
27

28. Decoders
• Example: determine when a binary 1001 occurs on the
inputs of a digital circuit
• Use AND gate; make sure that all of the inputs to the AND
gate are HIGH when the binary number 1001 occurs
IS 151 Digital Circuitry
28

29. Decoders
• Exercise: develop the logic required to
detect the binary code 10010 and produce
an active-LOW output (0)
IS 151 Digital Circuitry
29

30. Decoders - Application
• BCD-to-Decimal decoder
– Converts each BCD code into one of 10 possible decimal
digits
Decimal
Digit
BCD Code
A3 A2 A1 A0
BCD Decoding Function
0
0
0
0
0
A3’ A2’ A1’ A0’
1
0
0
0
1
2
0
0
1
0
3
0
0
1
1
4
0
1
0
0
5
0
1
0
1
6
0
1
1
0
7
0
1
1
1
8
1
0
0
0
9
1
0
0
1
IS 151 Digital Circuitry
30

31. Encoders
• A combinational logic circuit that performs
a reverse decoder function
• Accepts an active level on one of its inputs
(e.g. a decimal or octal digit) and converts
it to a coded output, e.g. BCD or binary
IS 151 Digital Circuitry
31

32. Encoders
• The Decimal-to-BCD Encoder (10-line-to-4-line encoder)
– Ten inputs (one for each decimal digit)
– Four outputs corresponding to the BCD code
• Logic symbol for a decimal-to-BCD encoder
Decimal
Input
DEC/BCD
0
1
2
3
1
4
2
5
4
6
8
7
8
9
BCD
Output
IS 151 Digital Circuitry
32

33. Encoders
• From the BCD/Decimal table, determine
the relationship between each BCD bit and
the decimal digits in order to analyse the
logic.
– Example
–
–
–
–
A3 = 8 + 9
A2 = 4 + 5 + 6 + 7
A1 = 2 + 3 + 6 + 7
A0 = 1 + 3 + 5 + 7 + 9
IS 151 Digital Circuitry
33

34. Encoders
• Example: if input line 9 is HIGH (assume
all others are LOW), it will produce a HIGH
on A3 and A0, and a LOW on A1and A2 –
which is 1001, meaning decimal 9.
IS 151 Digital Circuitry
34

35. Encoders - Exercise
• Implement the
logic circuit for the
10-line-to-4-line
encoder using the
logic expressions
for the BCD
codes A3 to A0
and inputs 0 to 9
IS 151 Digital Circuitry
35

36. Logic Functions Exercise
(Lab 3)
• Design and test a circuit to implement the
function of the full adder (refer to lecture)
IS 151 Digital Circuitry
36

37. • End of Lecture
IS 151 Digital Circuitry
37