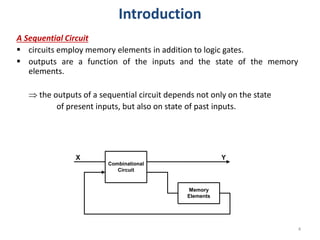
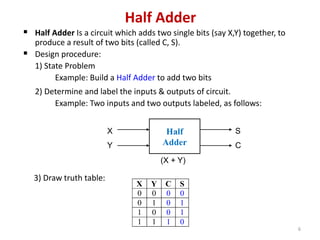
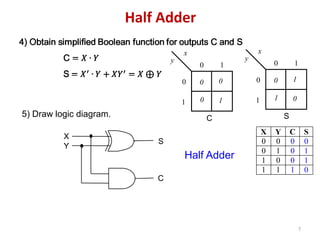
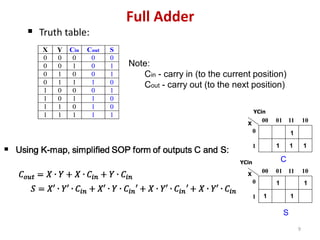
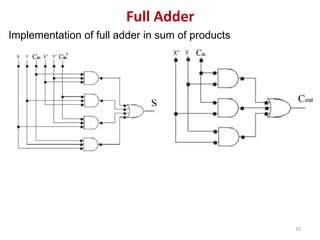
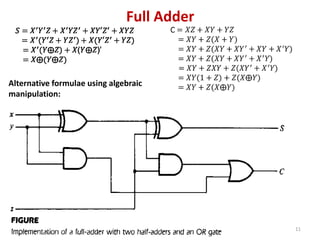
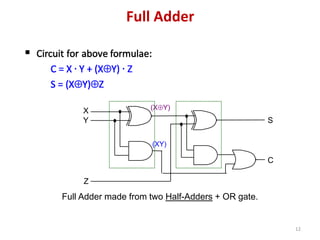
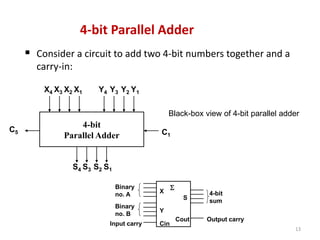
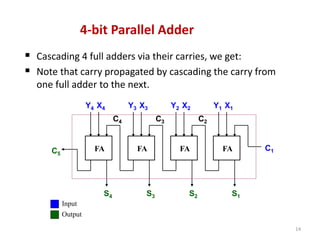
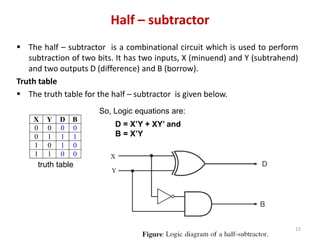
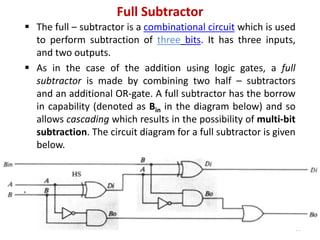
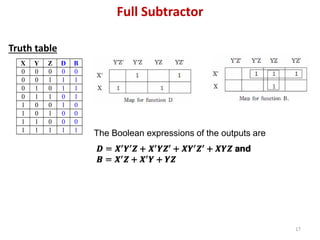
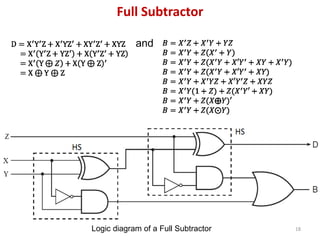
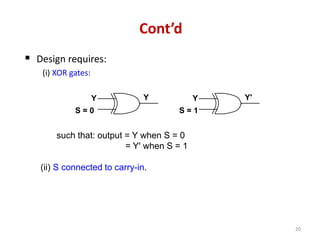
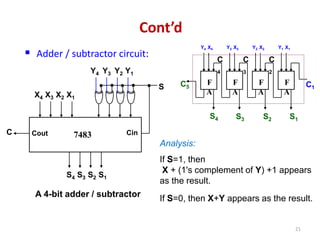
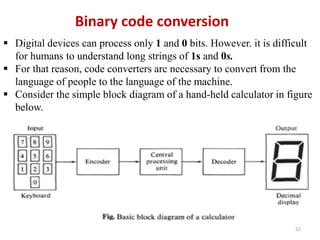
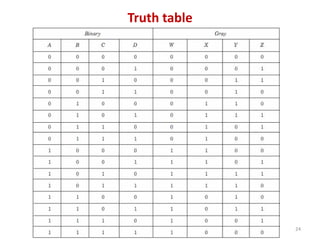
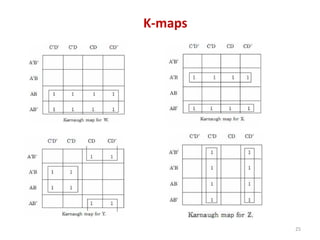
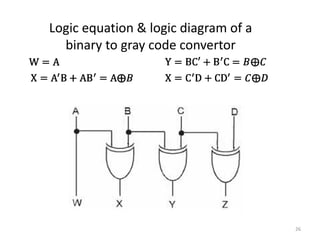
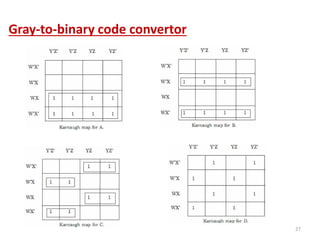
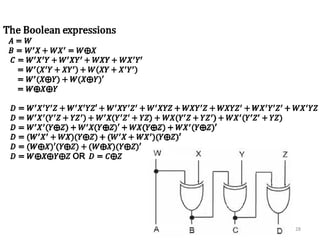
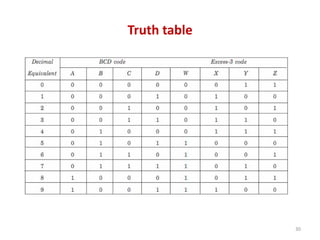
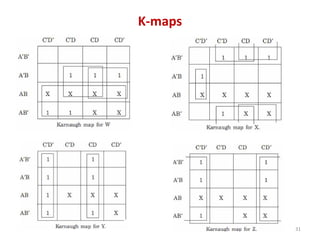
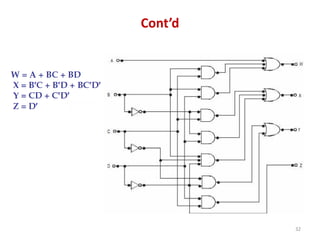
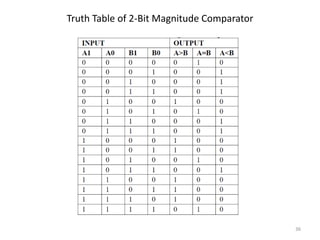
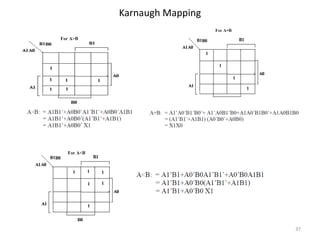
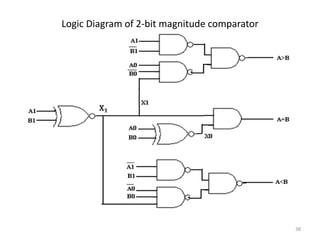
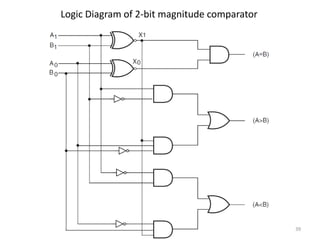
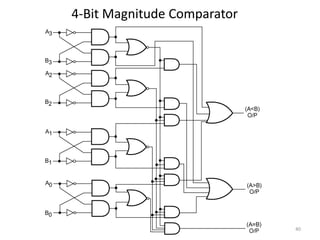
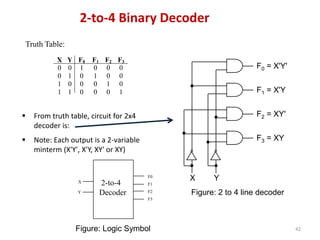
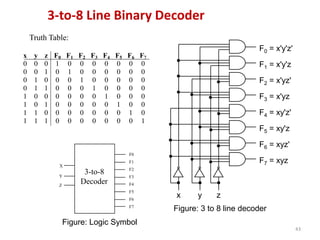
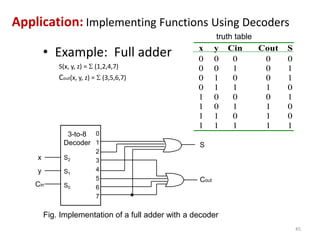
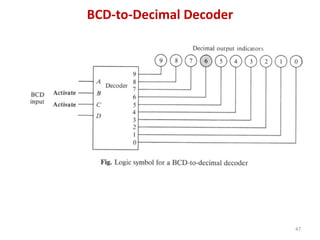
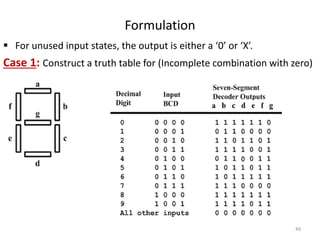
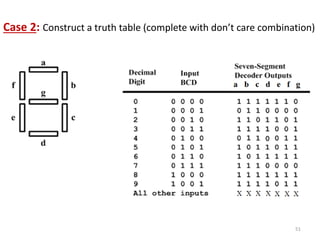
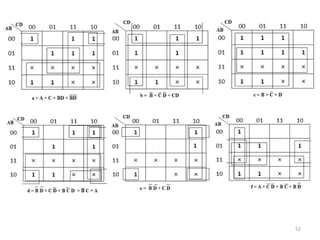
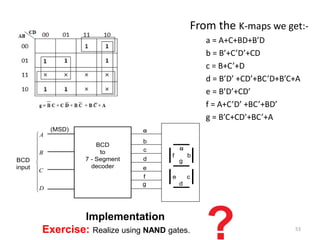
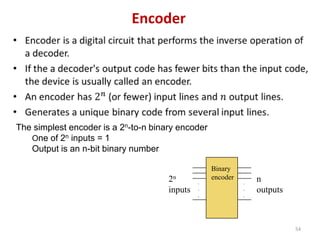
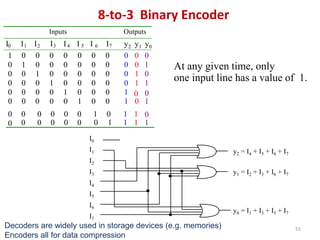
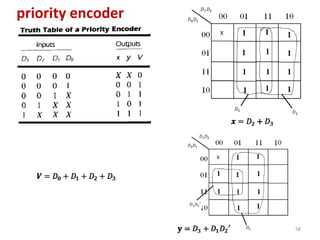
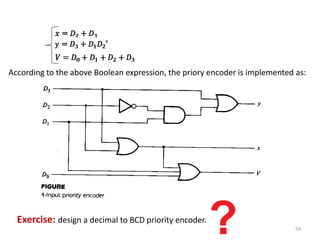
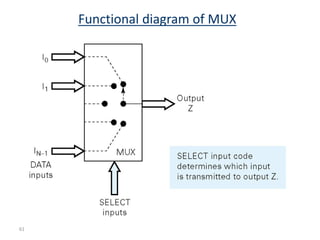
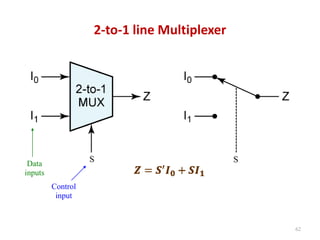
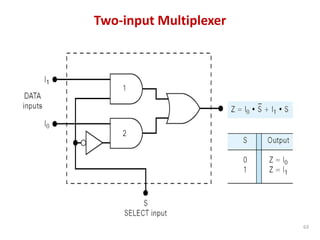
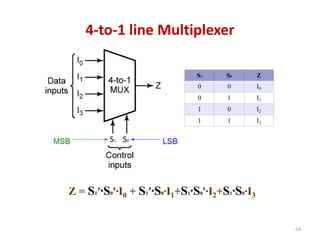
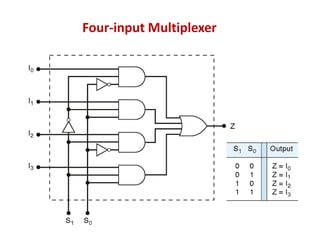
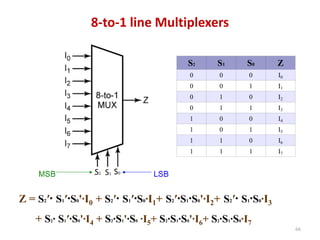
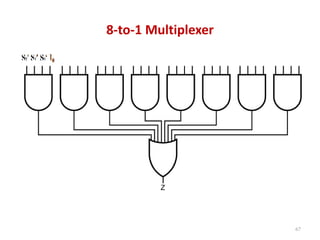
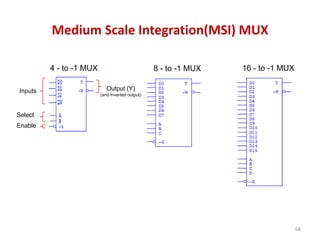
This document discusses combinational circuit design and provides examples of various combinational logic circuits. It begins with an introduction that defines combinational and sequential circuits. The remainder of the document provides details on specific combinational logic circuits including half adders, full adders, subtractors, encoders, decoders, multiplexers, comparators, and code converters. Worked examples are provided for each circuit type using truth tables, Karnaugh maps, and logic diagrams. Applications of decoders for implementing functions like a full adder are also described.

1. Chapter 4
Combinational circuit design
1

2. Chapter outline
 Introduction
 Adders
 Subtractors
 Binary code conversion
 Magnitude comparator
 Parity generator and checker
 Decoders
 Encoders
 Multiplexers
 Multiplexer tree
2
 Demultiplexers
 Demultiplexer tree
 Combinational Logic with MSI
and LSI
 Combinational logic design using
multiplexers
 Demultiplexers/Decoders and
their use in combinational logic
design

3. Introduction
Two types of Logic
Logic circuits for digital systems may be combinational or sequential.
A Combinational Circuit
 consists of logic gates whose outputs at any time are determined directly
from the present combination of inputs.
x0
xn
y0
yn
Inputs Outputs
.
.
.
.
Combinational
Logic Functions
F
3

4. A Sequential Circuit
 circuits employ memory elements in addition to logic gates.
 outputs are a function of the inputs and the state of the memory
elements.
 the outputs of a sequential circuit depends not only on the state
of present inputs, but also on state of past inputs.
Combinational
Circuit
Memory
Elements
X Y
4
Introduction

5. 5
Introduction
1. Problem description
2. Input/output of the circuit
3. Define truth table
4. Simplification for each output
5. Draw the circuit
In general we have to do the following steps:
Designing Combinational Circuits
Classification of Combinational Logic

6. 6
Half Adder
 Half Adder Is a circuit which adds two single bits (say X,Y) together, to
produce a result of two bits (called C, S).
 Design procedure:
1) State Problem
Example: Build a Half Adder to add two bits
2) Determine and label the inputs & outputs of circuit.
Example: Two inputs and two outputs labeled, as follows:
Half
Adder
X
Y
S
C
(X + Y)
3) Draw truth table:
X Y C S
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 0

7. 7
X Y C S
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 0
X
Y
S
C
Half Adder
5) Draw logic diagram.
y
0
1
0 1
0
1
x
0
0
y
0
1
0 1
0
0
x
1
1
Half Adder
C S

8. 8
Full Adder
 Half-adder adds up only two bits.
 To add two binary numbers, we need to add 3 bits (including the carry).
 Example:
1 1 1 carry
0 0 1 1 X
+ 0 1 1 1 Y
1 0 1 0 S
 Need Full Adder (so called as it can be made from two half-adders).
Full
Adder
X
Y
Cin
S
Cout
(X + Y + Cin)

9. 9
 Truth table:
X Y Cin Cout S
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 1
Note:
Cin - carry in (to the current position)
Cout - carry out (to the next position)
0
1
00 01 11 10
X
YCin
1
1
1
1
C
0
1
00 01 11 10
X
1
1
1
1
S
Full Adder
YCin

10. 10
Implementation of full adder in sum of products
Full Adder

11. 11
Full Adder
Alternative formulae using algebraic
manipulation:

12. 12
Full Adder made from two Half-Adders + OR gate.
(XY)
X
Y S
C
Z
(XY)
Full Adder

13. 13
4-bit Parallel Adder
 Consider a circuit to add two 4-bit numbers together and a
carry-in:
4-bit
Parallel Adder
C5 C1
X2 X1 Y4 Y3
S4 S3 S2 S1
Y2 Y1
X4 X3
Black-box view of 4-bit parallel adder
X
Y
S
Cout
S
Cin
Input carry
Binary
no. B
Binary
no. A
Output carry
4-bit
sum

14. 14
 Cascading 4 full adders via their carries, we get:
 Note that carry propagated by cascading the carry from
one full adder to the next.
C1
Y1 X1
S1
FA
C2
C5
Y2 X2
S2
FA
C3
Y3 X3
S3
FA
C4
Y4 X4
S4
FA
Output
Input
4-bit Parallel Adder

15. Half – subtractor
 The half – subtractor is a combinational circuit which is used to perform
subtraction of two bits. It has two inputs, X (minuend) and Y (subtrahend)
and two outputs D (difference) and B (borrow).
Truth table
 The truth table for the half – subtractor is given below.
15
X Y D B
0 0 0 0
0 1 1 1
1 0 1 0
1 1 0 0
So, Logic equations are:
D = X’Y + XY’ and
B = X’Y
truth table

16. Full Subtractor
 The full – subtractor is a combinational circuit which is used
to perform subtraction of three bits. It has three inputs,
and two outputs.
 As in the case of the addition using logic gates, a full
subtractor is made by combining two half – subtractors
and an additional OR-gate. A full subtractor has the borrow
in capability (denoted as Bin in the diagram below) and so
allows cascading which results in the possibility of multi-bit
subtraction. The circuit diagram for a full subtractor is given
below.
16

17. Truth table
17
X Y Z D B
0 0 0 0 0
0 0 1 1 1
0 1 0 1 1
0 1 1 0 1
1 0 0 1 0
1 0 1 0 0
1 1 0 0 0
1 1 1 1 1
The Boolean expressions of the outputs are
Full Subtractor

18. 18
Logic diagram of a Full Subtractor
and
Full Subtractor

19. 19
Addition/Subtraction in 2’s complement
Representation
Recall that:
X-Y = X + (-Y)
= X + (2’s complement of Y)
= X + (1’s complement of Y) +1
X+Y = X + (Y)

20. 20
Cont’d
 Design requires:
(i) XOR gates:
such that: output = Y when S = 0
= Y' when S = 1
(ii) S connected to carry-in.
S = 0
Y
Y
S = 1
Y'
Y

21. 21
Cont’d
 Adder / subtractor circuit:
Analysis:
If S=1, then
X + (1's complement of Y) +1 appears
as the result.
If S=0, then X+Y appears as the result.
7483
X2 X1
Y4 Y3 Y2 Y1
X4 X3
S2 S1
S4 S3
C
S
Cin
Cout
A 4-bit adder / subtractor
C1
Y1 X1
S1
F
A
C
2
C5
Y2 X2
S2
F
A
C
3
Y3 X3
S3
F
A
C
4
Y4 X4
S4
F
A

22. Binary code conversion
22
 Digital devices can process only 1 and 0 bits. However. it is difficult
for humans to understand long strings of 1s and 0s.
 For that reason, code converters arc necessary to convert from the
language of people to the language of the machine.
 Consider the simple block diagram of a hand-held calculator in figure
below.

23. Binary-to-gray Code Converter
• The bit combinations 4-bit binary code and its equivalent bit
combinations of gray code are listed in the table.
• The four bits of binary numbers are designated as A, B, C, and
D, and gray code bits are designated as W, X, Y, and Z.
• For transformation of binary numbers to gray, A, B, C, and D
are considered as inputs and W, X, Y, and Z are considered as
outputs.
23
Binary code conversion

24. Truth table
24

25. K-maps
25

26. Logic equation & logic diagram of a
binary to gray code convertor
26

27. Gray-to-binary code convertor
27

28. 28

29. BCD-to-excess-3 Code Converter
29
 The bit combinations of both the BCD (Binary Coded Decimal)
and Excess-3 codes represent decimal digits from 0 to 9.
Therefore each of the code systems contains four bits and so
there must be four input variables and four output variables.
 The symbols A, B, C, and D are designated as the bits of the
BCD system, and W, X, Y, and Z are designated as the bits of
the Excess-3 code system.
 It may be noted that though 16 combinations are possible
from four bits, both code systems use only 10 combinations.
The rest of the bit combinations never occur and are treated
as don’t-care conditions.

30. Truth table
30

31. K-maps
31

32. Cont’d
32

33. 33
Cont’d

34. Excess-3 - to – BCD Code Converter
 Assignment
34

35. Magnitude Comparator
35

36. Truth Table of 2-Bit Magnitude Comparator
36

37. Karnaugh Mapping
37

38. Logic Diagram of 2-bit magnitude comparator
38

39. 39
Logic Diagram of 2-bit magnitude comparator

40. 4-Bit Magnitude Comparator
40

41. Decoder
 Is a combinational circuit that converts binary information
from n input lines to a maximum of 2n unique output lines.
 For example if the number of input is n=3 the number of
output lines can be m=23 .
 It is also known as 1 of 8 because one output line is selected
out of 8 available lines:
 Binary decoders
– Converts an n-bit code to a single active output
– Only one output is a 1 for any given input
– Can be developed using AND/OR gates
3 to 8
decoder
enable 41

42. 2-to-4 Binary Decoder
 From truth table, circuit for 2x4
decoder is:
 Note: Each output is a 2-variable
minterm (X'Y', X'Y, XY' or XY)
X Y F0 F1 F2 F3
0 0 1 0 0 0
0 1 0 1 0 0
1 0 0 0 1 0
1 1 0 0 0 1
F0 = X'Y'
F1 = X'Y
F2 = XY'
F3 = XY
X Y
Truth Table:
2-to-4
Decoder
X
Y
F0
F1
F2
F3
42
Figure: 2 to 4 line decoder
Figure: Logic Symbol

43. 3-to-8 Line Binary Decoder
x y z F0 F1 F2 F3 F4 F5 F6 F7
0 0 0 1 0 0 0 0 0 0 0
0 0 1 0 1 0 0 0 0 0 0
0 1 0 0 0 1 0 0 0 0 0
0 1 1 0 0 0 1 0 0 0 0
1 0 0 0 0 0 0 1 0 0 0
1 0 1 0 0 0 0 0 1 0 0
1 1 0 0 0 0 0 0 0 1 0
1 1 1 0 0 0 0 0 0 0 1
F1 = x'y'z
x z
y
F0 = x'y'z'
F2 = x'yz'
F3 = x'yz
F5 = xy'z
F4 = xy'z'
F6 = xyz'
F7 = xyz
Truth Table:
3-to-8
Decoder
X
Y
F0
F1
F2
F3
F4
F5
F6
F7
Z
43
Figure: 3 to 8 line decoder
Figure: Logic Symbol

44. Decoder with Enable Line
 Decoders usually have an enable line.
 If enable=0 , decoder is OFF. It means all output lines
are zero.
 If enable=1, decoder is ON and depending on input,
the corresponding output line is 1, all other lines are 0.
44
3 to 8
decoder
enable

45. Application: Implementing Functions Using Decoders
• Example: Full adder
S(x, y, z) = S (1,2,4,7)
Cout(x, y, z) = S (3,5,6,7)
3-to-8
Decoder
S2
S1
S0
x
y
Cin
0
1
2
3
4
5
6
7
S
Cout
x y Cin Cout S
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 1
45
Fig. Implementation of a full adder with a decoder
truth table

46. 46
BCD-to-Decimal Decoder
A block diagram of such a decoder is in Figure below. The BCD (8421) code forms
the input on the left of the decoder. The 10 output lines are shown on the right. Only
one output line will be activated at a time. Indicators (LEDs or lamps) have been
attached to the output lines to help show which output is activated. For example
Inputs B and C ( B = 2s place, C = 4s place) are activated in the Figure below.
Line No. BCD Inputs Decimal Outputs
D C B A 0 1 2 3 4 5 6 7 8 9
Line 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0
Line 2 1 0 0 0 1 0 1 0 0 0 0 0 0 0 0
Line 3 2 0 0 1 0 0 0 1 0 0 0 0 0 0 0
Line 4 3 0 0 1 1 0 0 0 1 0 0 0 0 0 0
Line 5 4 0 1 0 0 0 0 0 0 1 0 0 0 0 0
Line 6 5 0 1 0 1 0 0 0 0 0 1 0 0 0 0
Line 7 6 0 1 1 0 0 0 0 0 0 0 1 0 0 0
Line 8 7 0 1 1 1 0 0 0 0 0 0 0 1 0 0
Line 9 8 1 0 0 0 0 0 0 0 0 0 0 0 1 0
Line
10
9 1 0 0 1 0 0 0 0 0 0 0 0 0 1

47. 47
BCD-to-Decimal Decoder

48. BCD-to-Seven-Segment Decoder
 Digital readouts on many digital products often use LED seven-
segment displays.
 Each digit is created by lighting the appropriate segments. The
segments are labeled with standard letters as a, b, c, d, e, f, g.
 The decoder takes a BCD input and outputs the correct code for the
seven-segment display.
48
 Input: A 4-bit binary value that is a BCD coded input.
 Outputs: 7 bits, a through g for each of the segments of the display.
 Operation: Decode the input to activate the correct segments.
Fig. Segment Identification and Decimal Number with typical display
a
b
f
c
d
e
g

49. Formulation
 For unused input states, the output is either a ‘0’ or ‘X’.
Case 1: Construct a truth table for (Incomplete combination with zero)
49

50. 50
a= A’C + A’BD + B’C’D’ + AB’C’
b= A’B’ + A’C’D’ + A’CD + AB’C’
c= A’B + A’D + B’C’D’ + AB’C’
d= A’C^D’ + A’B’C + B’C’D’ + AB’C’ + A’BC’D
e= A’CD’ + B’C’D’
f= A’BC’ + A’C’D’ + A’BD’ + AB’C’
g= A’CD’ + A’B’C + A’BC’ + AB’C’
Create a K-map for each output and get

51. 51
Case 2: Construct a truth table (complete with don’t care combination)

52. 52

53. 53
From the K-maps we get:-
a = A+C+BD+B’D
b = B’+C’D’+CD
c = B+C’+D
d = B’D’ +CD’+BC’D+B’C+A
e = B’D’+CD’
f = A+C’D’ +BC’+BD’
g = B’C+CD’+BC’+A
BCD
to
7 - Segment
decoder
a
b
f
c
d
e
g
a
b
c
d
e
f
g











D
C
B
A
BCD
input
(MSD)
Implementation
Exercise: Realize using NAND gates.

54. Encoder
54
.
.
.
.
.
.
2n
inputs
n
outputs
Binary
encoder
The simplest encoder is a 2n-to-n binary encoder
One of 2n inputs = 1
Output is an n-bit binary number

55. 8-to-3 Binary Encoder
At any given time, only
one input line has a value of 1.
Inputs Outputs
I0 I1 I2 I3 I4 I 5 I 6 I7 y2 y1 y0
1 0 0 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0 0 0 1
0 0 1 0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0 0 1 1
0 0 0 0 1 0 0 0 1 0 0
0 0 0 0 0 1 0 0 1 0 1
0 0 0 0 0 0 1 0 1 1 0
0 0 0 0 0 0 0 1 1 1 1
I0
I1
I2
I3
I4
I5
I6
I7
y0 = I1 + I3 + I5 + I7
y1 = I2 + I3 + I6 + I7
y2 = I4 + I5 + I6 + I7
55
Decoders are widely used in storage devices (e.g. memories)
Encoders all for data compression

56. Limitations of 8 to 3 encoder
1. If two inputs are active simultaneously, the output produces an
undefined combination. For example, if I3 and I6 are 1
simultaneously, the output of the encoder will be 111 because all
three o/ps are equal to 1. this does not represent binary 3 nor
binary 6. To resolve this ambiguity, encoder circuits must
establish a priority to ensure that only one input is encoded.
2. Another ambiguity in octal to binary encoder is that an o/p with
0’s is generated when all the inputs are 0. The problem is that an
o/p with all 0’s is also generated when I0 is equal to 1. This
ambiguity can be resolved by providing an additional o/p that
specifies the condition that none of the inputs are active.
56

57. priority encoder
57
 A priority function means that the encoder will give priority to the
highest order decimal digit in the inputs and ignore all other,

58. 58
priority encoder

59. 59
According to the above Boolean expression, the priory encoder is implemented as:
Exercise: design a decimal to BCD priority encoder.

60. Multiplexer
 Multiplexing means transmitting a large number of information
units over a smaller number of channels or lines.
 Multiplexer (MUX) is a combinational circuit that selects binary
information from one of the input lines and directs it to a single
output line
 Usually there are 2n input lines and n selection lines whose bit
combinations determine which input line is selected
 Multiplexers also known as Data Selectors
 For example for 2-to-1 multiplexer if selection S is zero then I0 has
the path to output and if S is one I1 has the path to output.
 Multiplexers are used in any application in which data must be
switched from multiple sources to a destination.
e.g., processor’s registers to ALU
60

61. 61
Functional diagram of MUX

62. 62
2-to-1 line Multiplexer
Data
inputs
Control
input

63. 63
Two-input Multiplexer

64. 64
4-to-1 line Multiplexer
Z = S1′∙S0'∙I0 + S1′∙S0∙I1+S1∙S0'∙I2+S1∙S0∙I3
S1 S0 Z
0 0 I0
0 1 I1
1 0 I2
1 1 I3

65. 65
Four-input Multiplexer

66. 66
8-to-1 line Multiplexers
S2 S1 S0 Z
0 0 0 I0
0 0 1 I1
0 1 0 I2
0 1 1 I3
1 0 0 I4
1 0 1 I5
1 1 0 I6
1 1 1 I7
Z = S2′∙ S1′∙S0'∙I0 + S2′∙ S1′∙S0∙I1+ S2′∙S1∙S0'∙I2+ S2′∙ S1∙S0∙I3
+ S2∙ S1′∙S0'∙I4 + S2∙S1'∙S0 ∙I5+ S2∙S1∙S0'∙I6+ S2∙S1∙S0∙I7

67. 67
8-to-1 Multiplexer

68. Medium Scale Integration(MSI) MUX
4 - to -1 MUX 8 - to -1 MUX 16 - to -1 MUX
68
Inputs
Select
Enable
Output (Y)
(and inverted output)