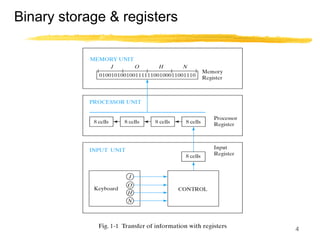
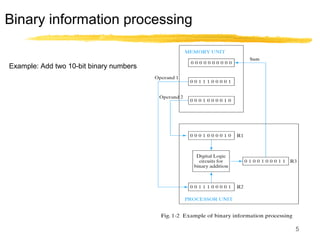
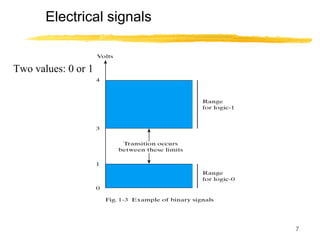
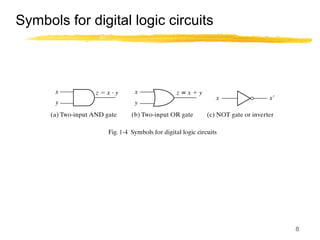
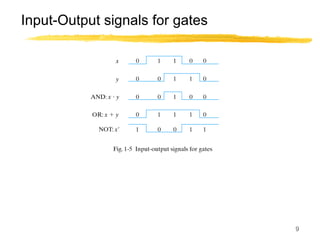
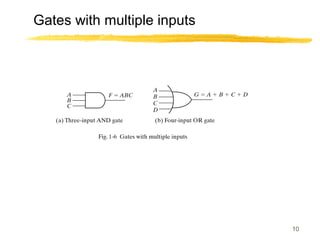
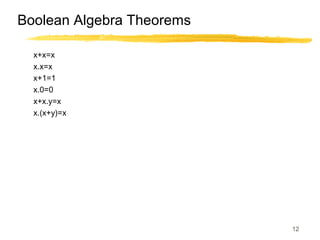
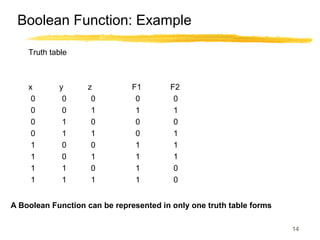
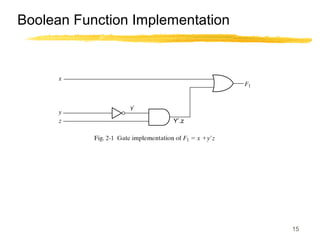
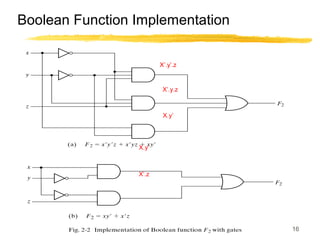
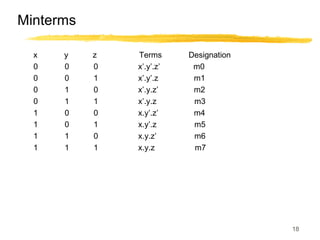
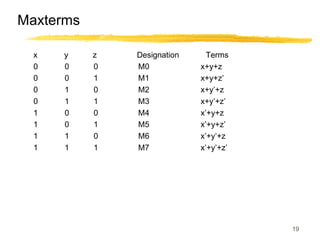
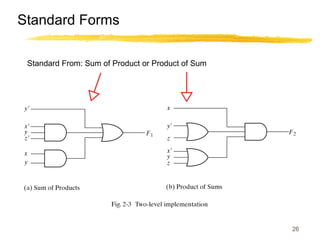
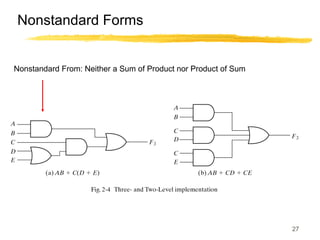
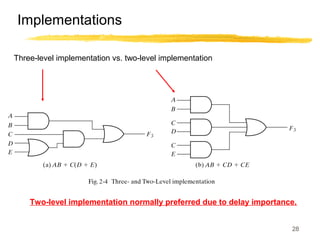
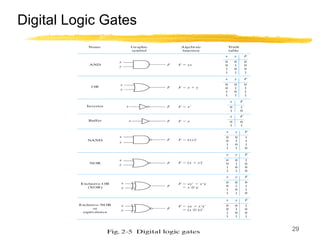
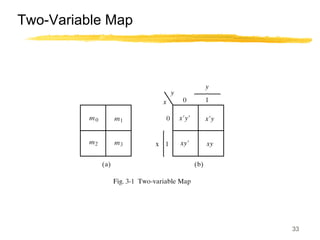
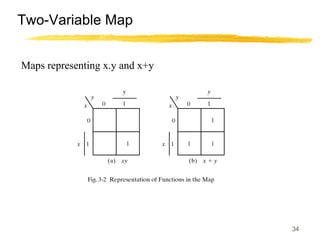
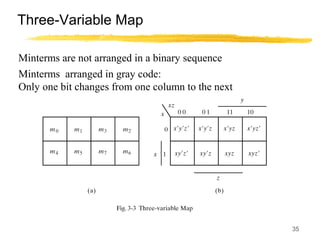
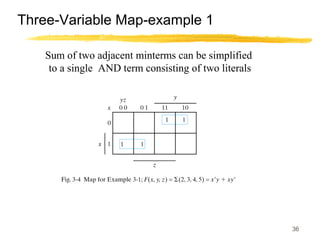
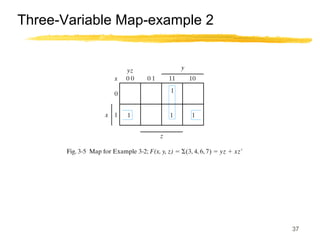
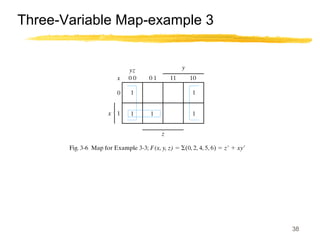
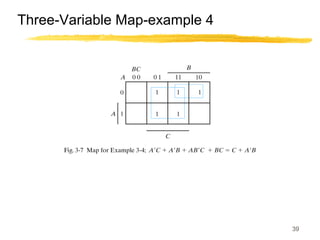
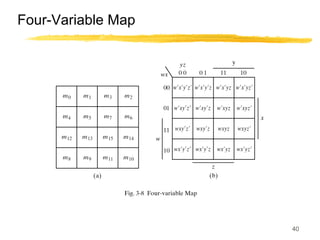
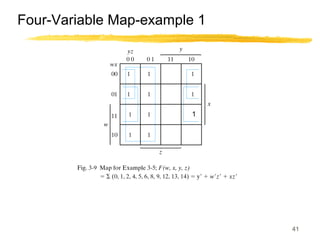
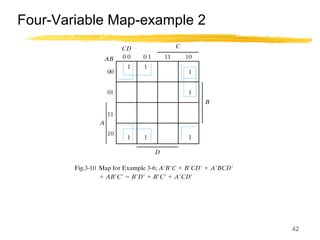
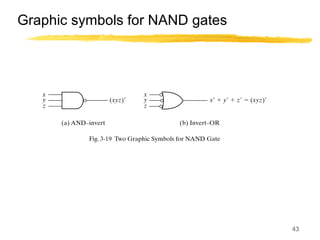
This lecture covers digital logic, binary storage, registers, Boolean algebra, and gate-level logic minimization. It introduces binary storage using bits and registers to store multiple bits. Binary logic uses variables that can only have two values (0 or 1) and logic gates that operate on inputs and produce an output. Boolean algebra allows representing logic functions with variables, operations, and standard forms like sum of products. Gate-level logic can be minimized using methods like the map method to reduce the number of gates. Key concepts are binary representation, logic gates, Boolean logic, standard forms, and logic minimization.