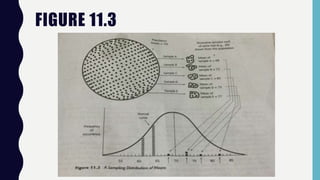
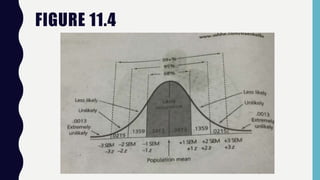
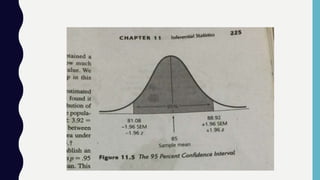
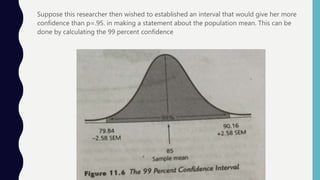
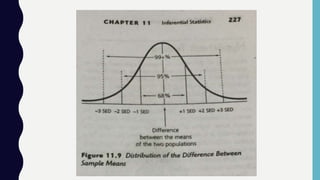
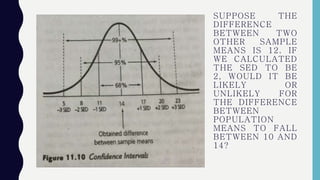
Inferential statistics allow researchers to make inferences about populations based on sample data, addressing concepts like sampling error, standard error, and confidence intervals. These statistics provide insights into population characteristics by analyzing the differences in sample means and estimating boundaries or limits for population means. Ultimately, the reliability of these inferences depends on the representativeness of the sample and the application of various statistical procedures like z scores.

1. INFERENTIAL
STATISTICS

2. OBJECTIVES
W H AT A R E I N F E R E N T I A L S TAT I S T I C S ?
T H E L O G I C O F I N F E R E N T I A L S TAT I S T I C S
• S A M P L I N G E R R O R
• D I S T R I B U T I O N O F S A M P L E M E A N S
• S TA N D A R D E R R O R O F T H E M E A N
• C O N F I D E N C E I N T E R VA L S
• C O N F I D E N C E I N T E R VA L S A N D P R O B A B I L I T Y
• C O M PA R I N G M O R E T H A N O N E S A M P L E
• T H E S TA N D A R D E R R O R O F T H E D I F F E R E N C E
B E T W E E N S A M P L E M E A N S

3. WHAT ARE INFERENTIAL STATISTICS?
Descriptive statistics are but one type of statistic that research
use to analyze their data . Many times they wish to make
inferences about a population based on a data they have
obtained from a sample. To do this, they use inferential
statistics.
INFERENTIAL STATISTICS are certain types of procedures that
allow a researchers to make inferences about a population
based on findings from a sample.
Making inferences about the populations on the basis of
random samples is what inferential statistics is all about.

4. Suppose a researcher administers a commercially
available IQ test to sample of 65 students selected from
a particular elementary school district and finds their
average score is 85. What does this tell her about the
IQ scores of the entire population of students in the
district? Does the average IQ score of students in the
district also equal 85? Or is this sample of students
different, on the average, from other students in the
district? If these students are different, how are they
different? Are their IQ scores higher –or lower?

5. When a sample is representative, all the characteristics
of the population are assumed to be present in the
sample in the same degree. No sampling procedure,
not even random sampling, guarantees a totally
representative sample, but the chance of obtaining one
is greater with random sampling than with any other
method. And the more a sample represents a
population, the more researchers are entitled to
assume that what they find out about the sample will
also be true of that population.

6. Suppose a researcher is interested in the difference between
males and females with respect to interest in history. He
hypothesizes that female students find history more interesting
than do male students. To testthe hypothesis, he decides to
perform the following study. He obtains one random sample of
30 male history students from the population of 500 male
tenth-grade students taking history in a nearby school district
and another random sample of 30 female history students from
the female population of 550 female tenth-grade history
students in the district.

7. LOGIC OF INFERENTIAL STATISTICS
POPULATION OF MALE
HISTORY STUDENTS
N = 500
POPULATION OF FEMALE
HISTORY STUDENTS
N = 550
SAMPLE 1
N = 30
SAMPLE 2
N=30

8. Will the mean score of the male group on the attitude test differ from the
mean score of the female group?
Is it reasonable to assume that each sample will give a fairly accurate
picture of its population?
On the other hand, the students in each sample are only a small portion
of their population, and only rarely is a sample absolutely identical to its
parent population on a given characteristic. The data the researcher
obtains from the two samples will depend on the individual students
selected to be in each sample.
So how can the researcher be sure that any particular sample he has
selected is, indeed, a representative one?

9. The data the researcher obtains from the two samples will
depend on the individuals selected to be in each sample
Samples are not likely to identical to their parent populations.
The difference between a sample and its population is referred
to as sampling error.
No two samples from the same population will be the same in
all their characteristics. Two different samples from the same
population will not be identical: They will be composed of diff.
individuals, they will have different scores on a test(or other
measure) and they will probably have different sample means

10. FIGURE 11.2

11. DISTRIBUTION OF SAMPLE MEANS
Large collections of random samples do pattern themselves in such a way
that is possible for researchers to predict accurately some characteristics
of the population from which the sample was selected. Were we able to
select an infinite number of random samples ( all of the same size ) from a
population, calculate the mean of each, and then arrange these means
into a frequency polygon, we would find that they shaped themselves into
a familiar pattern.
The means of a large number of random samples tend to be normally
distributed, unless the size of each of the sample is small ( n<30). Once
n=30, the distribution of sample means is very nearly normal, even if the
population is not normally distributed.

12. Like all normal distributions, a distribution of
sample means (called a sampling distribution) has
its own mean and a standard deviation. The mean
of a sampling distribution(the “mean of the
means”) is equal to the mean of the population. In
an infinite number of samples, the results will vary.
Consider the number 1,2 and 3. The population
mean is 2. Now take all of the possible types of
samples of size two. How many would there be?
Does the mean of this sampling distribution equal
to the whole population?

13. FIGURE 11.3

14. STANDARD ERROR OF THE MEAN
Is the standard deviation of a sampling distribution. As in all
normal distributions, therefore the 68-99-99.7 rule holds:
approximately 68% of the sample means fall ±1 SEM,
approximately 95% percent fall between ±2 SEM and 99.7% fall
between ±3 SEM.
If we know or can accurately estimate the mean and the
standard deviation of the sampling distribution, we can
determine whether it is likely or unlikely that a particular
sample mean could be obtained from that population.

15. FIGURE 11.4

16. It is possible to use z scores to describe the position of
any particular sample mean within a distribution of
sample means. Z scores is the simplest form of
standard score. A z score simply states how far a
score(or mean) differs from the mean of scores(or
means) in standard deviation units. One z score = 1
standard deviation. The z score tells a researcher
exactly where a particular sample is located related to
all other sample means that could have obtained.

17. ESTIMATING THE STANDARD ERROR
OF THE MEAN
𝑆𝐸𝑀 =
𝑆𝐷
𝑛 − 1

18. A LITTLE REVIEW
1. The sampling distribution of the mean ( or any descriptive statistics) is the
distribution of the means ( or other statistic) obtained (theoretically) from an
infinitely large number of samples of the same size.
2. The shape of the sampling distribution in many (but not all) cases is the
shape of the normal distribution.
3. The SEM ( Standard Error of the Mean)- that is, the standard deviation of a
sampling distribution of means--- can be estimated by dividing the standard
deviation of the sample by the square root of the sample size minus one.
4. The frequency with which a particular sample mean will occur an be
estimated by using z scores based on sample data to indicate its position in
the sampling distribution

19. CONFIDENCE INTERVALS
We can use the SEM to indicate boundaries or limits, within which the
population mean lies. Such boundaries are called confidence intervals. How
are they determined?
Let us return to the example of the researcher who administered and IQ test.
You will recall that she obtained a sample mean of 85 and wanted to know
how much the population mean might differ from this value. We are now in
a position to give her some help in this regard.
Let us assume that we have calculated the estimated standard error of the
mean for her sample and found it to equal to 2.0

21. Suppose this researcher then wished to established an interval that would give her more
confidence than p=.95. in making a statement about the population mean. This can be
done by calculating the 99 percent confidence

22. Our researcher can now answer her question about approximately how
much the population mean differs from the sample mean. While she
cannot know exactly the population mean is, she can indicate the
‘boundaries’ or limits within which it is likely to fall. To repeat, these limits
are called confidence intervals.
The 95 percent confidence interval spans a segment on the horizontal axis
that we are 95 percent certain contains the population mean.
The 99 percent confidence interval spans a segment on the horizontal axis
within which we are even more certain ( 99 percent certain) that the
population mean falls.

24. CONFIDENCE INTERVALS AND
PROBABILITY
Probability is nothing more than predicted relative occurrence, or
relative frequency. 5 in 100 is an example of probability
The probability of the population mean being outside the 81.08-
88.92 limits (95 percent confidence interval) is only 5 in 100
The probability of the population mean being outside the 79.84-
90.16 limits (99 percent confidence interval) is even less--- 1 in 100

25. COMPARING MORE THAN ONE
SAMPLE
For example, a researcher might want to determine if there is a
difference in attitude between 4th grade boys and girls in
mathematics; whether there is a difference in achievement
between students taught by the discussion method as
compared to the lecture method; and so forth
For example, if a difference between means is found between
the test scores of two samples in a study, a researcher wants to
know if a difference exists in the populations from which the
two samples were selected.

26. DOES A SAMPLE DIFFERENCE REFLECT A
POPULATION DIFFERENCE?
Is the difference we have found a likely or an unlikely occurrence?
POPULATION MEAN
???
POPULATION MEAN
???
SAMPLE A
Mean = 25
SAMPLE B
Mean = 22

27. THE STANDARD ERROR OF THE
DIFFERENCE BETWEEN SAMPLE MEANS
Differences between sample means are also likely to be
normally distributed. The distribution of differences between
sample means also has its own mean and standard deviation.
The mean of the sampling distribution of differences between
sample means of the two populations. The standard deviation
of this distribution is called the standard error of the difference
(SED)
𝑆𝐸𝐷 = (𝑆𝐸𝑀1)2 + (𝑆𝐸𝑀2)2

29. SUPPOSE THE
DIFFERENCE
BETWEEN TWO
OTHER SAMPLE
MEANS IS 12. IF
WE CALCULATED
THE SED TO BE
2, WOULD IT BE
LIKELY OR
UNLIKELY FOR
THE DIFFERENCE
BETWEEN
POPULATION
MEANS TO FALL
BETWEEN 10 AND
14?