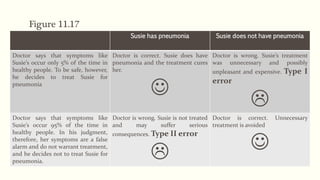
The document reviews hypothesis testing, detailing the distinction between research and null hypotheses and the process of determining statistical significance. It emphasizes the importance of understanding practical versus statistical significance and the potential for errors in hypothesis testing. Additionally, the document explains one-tailed and two-tailed tests, highlighting the need for careful interpretation of results.

1. HYPOTHESIS
TESTING

2. A REVIEW
 A hypothesis predict a relationship
 There are techniques for examining data for the existence of relationships
 Can be examined through three procedures: a comparison of means, a
correlation, or a crossbreak table
 The logic of Inferential statistics applies to any particular form of a hypothesis
and to many procedure used to examine data
 In hypothesis testing, instead of determining the boundaries within which the
population mean can be said to fall, a researcher determines the likelihood of
obtaining a sample value if there is no relationship in the populations from
which the samples were drawn
 The researcher formulates both a research hypothesis and a null hypothesis

3. Null HYPOTHESIS and Research HYPOTHESIS
Research Hypothesis specifies the predicted outcome of the study. Many research
hypothesis predict the nature of the relationship for the researcher thinks exists in
the population; for example;
“The population mean of students using method A is greater than the
population mean of students using method B”
Null Hypothesis most commonly used specifies there is no relationship in the
population; for example;
“There is no difference between the population mean of students using
method A and the population mean of students using method B”

4. THE LOGICAL SEQUENCE OF HYPOTHESIS TESTING
The researcher will test the null hypothesis. The same info is
needed as before: the knowledge that the sampling distribution is
normal, and the calculated standard error of the difference (SED)
What is different in a hypothesis test is that instead of using the
obtained sample value as the mean of sampling distribution we use
zero.*
We then can determine the probability of obtaining a particular
sample value by seeing where such a value falls on the sampling
distribution.
If the probability is small, the null hypothesis is rejected, thereby
providing support for the research hypothesis. The results are said to
be statistically significant.

5. A small continuation
It is customary in educational research to view as unlikely any
outcome that has a probability of .05 (p=.05) or less. This referred to
as the 0.5 level of significance.
When we reject a null hypothesis at the .05 level, we are saying
that the probability of obtaining such an outcome is only 5 times (or
less) in 100.
Some researchers prefer to be even more stringent and choose a
.01 level of significance.
When a null hypothesis is rejected at the .01 level, it means that
the likelihood of obtaining the outcome is only 1 time (or less) in 100.

6. A REVIEW of the Logical Sequence of Hypothesis Testing
1. State the research hypothesis (e.g., “There is a difference between the
population mean of students using method A and the population mean of
students using method B”)
2. State the null hypothesis (e.g., “There is no difference between the population
mean of students using method A and the population mean of students using
method B”, or “The difference between the two population means is zero”)
3. Determine the sample statistics pertinent to the hypothesis (e.g., the mean of
sample A and the mean of sample B)
4. Determine the probability of obtaining the sample results (i.e., the difference
between the mean of sample A and the mean of sample B)

7. 5. If the probability is small, reject the null hypothesis, thus affirming
the research hypothesis
6. If the probability is large, do not reject the null hypothesis, which
means you cannot affirm the research hypothesis

8. PRACTICAL VERSUS
STATISTICAL
SIGNIFICANCE
The fact that a result is statistically significant does not mean that it has any practical or educational value in
the real world in which we all work and live.

9. Statistical Significance
only means that one’s results are likely to occur by chance less
than a certain percentage of the time, say 5 percent. This only means
the observed relationship most likely would not be zero in the
population.
but it does not mean necessarily that it is IMPORTANT!
whenever we have a large enough random sample, almost any
result will turn out to be statistically significant. Thus a very small
correlation coefficient, for example, may turn out to be statistically
significant but have little (if any) practical significance
in a similar sense, a very small difference in means may yield a
statistically significant result but have a little educational import

10. Ironically, the fact the most educational studies involve smaller
samples may actually be an advantage when it comes to practical
significance. Because smaller sample size makes it harder to detect a
difference even there is one in a population, a larger difference in
means is therefore required to reject the null hypothesis.
This is so because a smaller sample results in a larger standard
error of the difference in means (SED). Therefore, a larger difference in
means is required to reach the significance level.
One should always take care in interpreting results----- just
because one brand of radios is significantly more powerful than
another brans statistically does not mean than those looking for radio
should rush to but the first brand.

11. One- Tailed Tests
To determine the probability associated with this outcome, we must
know whether the researcher’s hypothesis was a directional or a
nondirectional one. If the hypothesis was directional, the researcher specified
ahead of time which group would have the higher mean.
The researcher would be supported only if the sample A were higher
than the mean of sample B. The researcher must decide beforehand that he
or she will subtract the mean of sample B from sample A.
A large difference between sample means in the opposite direction
would not support the research hypothesis.
The researchers’ hypothesis can be supported only if he or she obtains
a positive difference between the sample means, the researcher is justified in
using only the positive tail of the sampling distribution to locate the obtained
difference

12. Figure 11.15

13. Figure 11.16
The researcher would not have specified beforehand which group would have
the higher mean. The hypothesis would then be supported by a suitable difference in
either tail. This is called a two-tailed test of significance

14. USE OF THE NULL HYPOTHESIS: AN EVALUATION
There appears to be much misunderstanding regarding the use of the null
hypothesis.
1. It is often stated in place of a research hypothesis
2. There is nothing sacred about the customary .05 and .01 significance levels.
TYPE II ERROR – error results when a researcher fails to reject a null
hypothesis that is false
TYPE I ERROR- error results when a researcher rejects a null hypothesis that
is true.

15. Figure 11.17
Susie has pneumonia Susie does not have pneumonia
Doctor says that symptoms like
Susie’s occur only 5% of the time in
healthy people. To be safe, however,
he decides to treat Susie for
pneumonia
Doctor is correct. Susie does have
pneumonia and the treatment cures
her.

Doctor is wrong. Susie’s treatment
was unnecessary and possibly
unpleasant and expensive. Type I
error

Doctor says that symptoms like
Susie’s occur 95% of the time in
healthy people. In his judgment,
therefore, her symptoms are a false
alarm and do not warrant treatment,
and he decides not to treat Susie for
pneumonia.
Doctor is wrong. Susie is not treated
and may suffer serious
consequences. Type II error

Doctor is correct. Unnecessary
treatment is avoided
