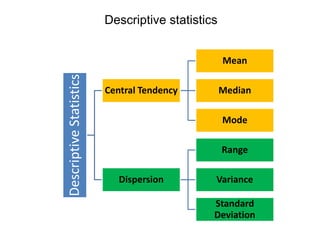
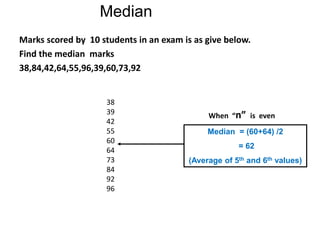
This document defines and provides examples of key concepts in descriptive statistics including: - Central tendency measures like mean, median, and mode - Dispersion measures like range, variance, and standard deviation It explains how to calculate each measure and interprets what each conveys about the distribution of values in a data set. Outliers are shown to affect the mean but not the median.

1. DESCRIPTIVE STATISTICS
K MURUGESAN

2. DescriptiveStatistics
Central Tendency
Mean
Median
Mode
Dispersion
Range
Variance
Standard
Deviation
Descriptive statistics

3. Central Tendency
• Mean is the average or arithmetic mean of the data.
• Median is the middle value of the data set, when the
data set is arranged in the ascending or descending order.
• Mode is the most frequently observed value(s).

4. • Range is the difference between highest and lowest observations in the data set
• Variance is a measure of spread of a data set
It is calculated as the average squared deviation of each number from mean of a data set.
• Standard Deviation is the Square Root of the Variance.
Dispersion

5. Mean
Variance
Standard
Deviation
X
n
x
n
i
i


1

6. The marks obtained by 10 students in a subject are as
given below
9,31,35,34,37,32,100,33,30,100
Average Marks:
=(9+31+35+34+37+32+100+33+30+100)/10
=44
Effect of outliers on Mean

7. The marks obtained by 8 students in a subject are as
given below
31,35,34,37,32,38,33,30
Average Marks:
=(31+35+34+37+32+38+33+30)/8
=33.75
Mean

8. The marks obtained by 10 students in a subject are as
given below
9,31,35,34,37,32,100,33,30,100
Average Marks:
=(9+31+35+34+37+32+100+33+30+100)/10
=44.1
Effect of outliers on Mean

9. • The middle value when a variable’s values are ranked in
ascending/ descending order
If n is odd;
Median is ((n-1)/2)+1th value
If n is even;
Median is Average of {(n/2), (n/2)+1} values
Median

10. Median = 60
(six cases above, six below)
Marks scored by 13 students in an exam is as give below.
Find the median marks
35,90,40,62,54,95,38,60,73,92,51,32,74
Median
32
35
38
40
51
54
60
62
73
74
90
92
95
When “n” is odd

11. Median = (60+64) /2
= 62
(Average of 5th and 6th values)
Marks scored by 10 students in an exam is as give below.
Find the median marks
38,84,42,64,55,96,39,60,73,92
Median
38
39
42
55
60
64
73
84
92
96
When “n” is even

12. The marks obtained by 10 students in a subject are as
given below
9,31,35,34,37,32,100,33,30,100
Median: 9,30,31,32,33,34,35,37,100,100
Effect of outliers on Median
= (33+34)/2
=33.5
Median is not influenced by outliers

13. The mode for a data set is the element that occurs the most often.
More than one mode is possible for a data set.
It is also possible that a data set may not have a mode at all.
Example-1:
Data set: 2,5,4,7,8,9,4,3,6,4,7,8,6,4,9,2
Mode: 4
Example-2:
Data set: 10,25,15,30,25,45,50,15,40,35
Modes: 25, 15
Mode

14. Range
Range = Largest value – Smallest value
The spread, or the difference, between the lowest and highest values of a variable.
31,35,34,37,32,38,33,30
Data set
Range = 38 - 30
= 8

15. Variance
A measure of the spread of the recorded values on a variable.
The larger the variance, the further the individual values are from the mean.
The smaller the variance, the closer the individual values are to the mean.
Mean
Mean

16. The square root of the variance (Standard deviation) reveals the
average deviation of the observations from the mean.
Standard deviation
 
1
1
2




n
xx
s
n
i
i

17. • The larger the standard deviation, the more
spread out the data is.
Interpretation of standard deviation

18. THANK YOU