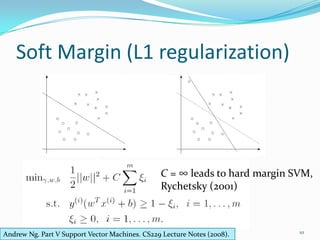
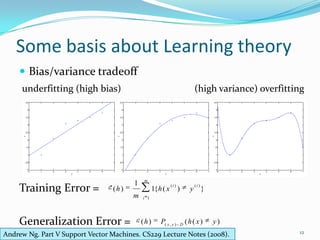
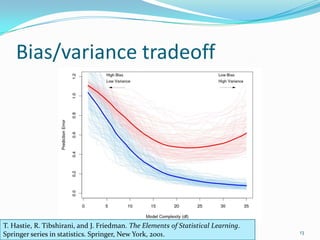
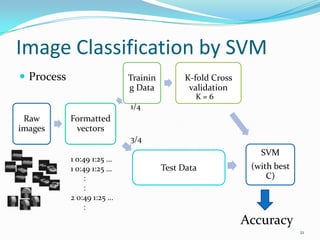
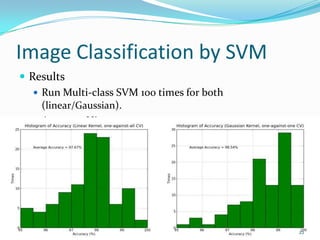
This document discusses support vector machines and their application to image classification. It provides an overview of SVM concepts like functional and geometric margins, optimization to maximize margins, Lagrangian duality, kernels, soft margins, and bias-variance tradeoff. It also covers multiclass SVM approaches, dimensionality reduction techniques, model selection via cross-validation, and results from applying SVM to an image classification problem.

1. Image Classification and Support Vector MachineShao-Chuan WangCITI, Academia Sinica1

2. Outline (1/2)Quick Review of SVMIntuitionFunctional margin and geometric marginOptimal margin classifierGeneralized Lagrangian multiplier methodsLagrangian dualityKernel and feature mappingSoft Margin ( l1 regularization)2

3. Outline (2/2)Some basis about Learning theoryBias/variance tradeoff (underfitting vs overfitting)Chernoff bound and VC dimensionModel selectionCross validationDimension ReductionMulticlass SVMOne against oneOne against allImage Classification by SVMProcessResults3

4. Intuition: MarginsFunctional MarginGeometric MarginWe feel more confident when functional margin is largerNote that scaling on w, b won’t change the plane.4Andrew Ng. Part V Support Vector Machines. CS229 Lecture Notes (2008).

5. Maximize marginsOptimization problem: maximize minimal geometric margin under constraints.Introduce scaling factor such that5Andrew Ng. Part V Support Vector Machines. CS229 Lecture Notes (2008).

6. Lagrange dualityPrimal optimization problem:Generalized LagrangianPrimal optimization problem (equivalent form)Dual optimization problem:6Andrew Ng. Part V Support Vector Machines. CS229 Lecture Notes (2008).

7. Dual ProblemThe necessary conditions that equality holds:f, giare convex, and hi are affine.KKT conditions.7Andrew Ng. Part V Support Vector Machines. CS229 Lecture Notes (2008).

8. Optimal margin classifiersIts LagrangianIts dual problem8Andrew Ng. Part V Support Vector Machines. CS229 Lecture Notes (2008).

9. Kernel and feature mappingKernel:Positive semi-definiteSymmetricFor example:Loose Intuition“similarity” between features9Andrew Ng. Part V Support Vector Machines. CS229 Lecture Notes (2008).

10. Soft Margin (L1 regularization)C = ∞ leads to hard margin SVM, Rychetsky (2001)10Andrew Ng. Part V Support Vector Machines. CS229 Lecture Notes (2008).

11. Why doesn’t my model fit well on test data ?11

12. Some basis about Learning theoryBias/variance tradeoffunderfitting (high bias) (high variance) overfittingTraining Error = Generalization Error =12Andrew Ng. Part V Support Vector Machines. CS229 Lecture Notes (2008).

13. Bias/variance tradeoffT. Hastie, R. Tibshirani, and J. Friedman. The Elements of Statistical Learning. Springer series in statistics. Springer, New York, 2001.13

14. Is training error a good estimator of generalization error?14

15. Chernoff bound (|H|=finite)Lemma: Assume Z1, Z2, …, Zmare drawn iid from Bernoulli(φ), and and let γ > 0 be fixed. Then, based on this lemma, one can find, with probability 1-δ(k = # of hypotheses)15Andrew Ng. Part VI Learning Theory. CS229 Lecture Notes (2008).

16. Chernoff bound (|H|=infinite)VC Dimension d : The size of largest set that H can shatter.e.g. H = linear classifiersin 2-DVC(H) = 3With probability at least 1-δ,16Andrew Ng. Part VI Learning Theory. CS229 Lecture Notes (2008).

17. Model SelectionCross Validation: Estimator of generalization errorK-fold: train on k-1 pieces, test on the remaining (here we will get one test error estimation). Average k test error estimations, say, 2%. Then 2% is the estimation of generalization error for this machine learner.Leave-one-out cross validation (m-fold, m = training sample size)traintrainvalidatetraintraintrain17

18. Model SelectionLoop possible parameters:Pick one set of parameter, e.g. C = 2.0Do cross validation, get a error estimationPick the Cbest (with minimal error estimation) as the parameter18

19. Dimensionality ReductionWhich features are more “important”?Wrapper model feature selectionForward/backward search: add/remove a feature at a time, then evaluate the model with the new feature set.Filter feature selectionCompute score S(i) that measures how informative xi is about the class label yS(i) can be correlation Corr(x_i, y), or mutual information MI(x_i, y), etc.Principal Component Analysis (PCA)Vector Quantization (VQ)19

20. Multiclass SVMOne against oneThere are binary SVMs. (1v2, 1v3, …)To predict, each SVM can vote between 2 classes.One against allThere are k binary SVMs. (1 v rest, 2 v rest, …)To predict, evaluate , pick the largest.Multiclass SVM by solving ONE optimization problemK = 135321123456K = 3poll Crammer, K., & Singer, Y. (2001). On the algorithmic implementation of multiclass kernel-based vector machines. JMLR, 2, 265-292.20

21. Image Classification by SVMProcessK = 61/4 3/41 0:49 1:25 …1 0:49 1:25 …： ：2 0:49 1:25 …：Test DataAccuracy21

22. Image Classification by SVMResultsRun Multi-class SVM 100 times for both (linear/Gaussian).Accuracy Histogram22

23. Image Classification by SVMIf we throw object data that the machine never saw before.23

24. ~ Thank You ~Shao-Chuan WangCITI, Academia Sinica24