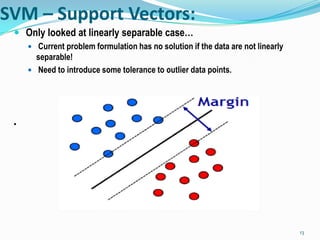
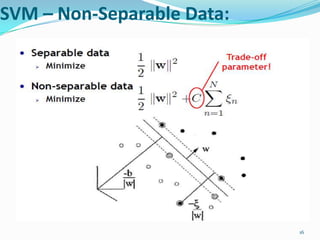
This document discusses support vector machines (SVMs) for classification. It explains that SVMs find the optimal separating hyperplane that maximizes the margin between positive and negative examples. This is formulated as a convex optimization problem. Both primal and dual formulations are presented, with the dual having fewer variables that scale with the number of examples rather than dimensions. Methods for handling non-separable data using soft margins and kernels for nonlinear classification are also summarized. Popular kernel functions like polynomial and Gaussian kernels are mentioned.

1. Musa Al hawamdah
128129001011
1

2. Topics :
 Linear Support Vector Machines
- Lagrangian (primal) formulation
- Dual formulation
- Discussion
 Linearly non-separable case
- Soft-margin classification
 Nonlinear Support Vector Machines
- Nonlinear basis functions
- The Kernel trick
- Mercer’s condition
- Popular kernels
2

3. Support Vector Machine (SVM):
 Basic idea:
- The SVM tries to find a classifier which
maximizes the margin between pos. and
neg. data points.
- Up to now: consider linear classifiers
• Formulation as a convex optimization problem
Find the hyperplane satisfying
3

4. SVM – Primal Formulation:
 • Lagrangian primal form:
• The solution of Lp needs to fulfill the KKT conditions
- Necessary and sufficient conditions
4

5. SVM – Solution:
 Solution for the hyperplane
** Computed as a linear combination of the training examples:
**Sparse solution: only for some points, the support vectors
⇒ Only the SVs actually influence the decision boundary!
**Compute b by averaging over all support vectors:
5

6. SVM – Support Vectors:
 The training points for which an > 0 are called “support vectors”.
 Graphical interpretation:
** The support vectors are the points on the margin.
**They define the margin and thus the hyperplane.
⇒ All other data points can be discarded!
•
6

7. SVM – Discussion (Part 1):
 Linear SVM:
 Linear classifier
 Approximative implementation of the SRM principle.
 In case of separable data, the SVM produces an empirical risk of zero with minimal value of the
VC confidence
(i.e. a classifier minimizing the upper bound on the actual risk).
 SVMs thus have a “guaranteed” generalization capability.
 Formulation as convex optimization problem.
⇒ Globally optimal solution!
 Primal form formulation:
 Solution to quadratic prog. problem in M variables is in .
 Here: D variables ⇒
 Problem: scaling with high-dim. data (“curse of dimensionality”)
7

8. SVM – Dual Formulation:
8

9. SVM – Dual Formulation:
9

10. SVM – Dual Formulation:
•
10

11. SVM – Dual Formulation:
11

12. SVM – Discussion (Part 2):
 Dual form formulation
 In going to the dual, we now have a problem in N variables (an).
 Isn’t this worse??? We penalize large training sets!
 However…
12

13. SVM – Support Vectors:
 Only looked at linearly separable case…
 Current problem formulation has no solution if the data are not linearly
separable!
 Need to introduce some tolerance to outlier data points.
•
13

14. SVM – Non-Separable Data:
14

15. SVM – Soft-Margin Classification:
15

16. SVM – Non-Separable Data:
16

17. SVM – New Primal Formulation:
17

18. SVM – New Dual Formulation
18

19. SVM – New Solution:
19

20. Nonlinear SVM:
20

21. Another Example
• Non-separable by a hyperplane in 2D:
21

22. • Separable by a surface in 3D
22

23. Nonlinear SVM – Feature Spaces
 • General idea: The original input space can be mapped to some higher-
dimensional feature space where the training set is separable:
23

24. Nonlinear SVM:
24

25. What Could This Look Like?
25

26. Problem with High-dim. Basis
Functions
26

27. Solution: The Kernel Trick:
27

28. Back to Our Previous Example…
28

29. SVMs with Kernels:
29

30. Which Functions are Valid
Kernels?
 Mercer’s theorem (modernized version):
 Every positive definite symmetric function is a kernel.
 Positive definite symmetric functions correspond to a
positive definite symmetric Gram matrix:
30

31. Kernels Fulfilling Mercer’s
Condition:
31

32. THANK YOU
32