The document discusses edge detection methods including gradient based approaches like Sobel and zero crossing based techniques like Laplacian of Gaussian. It proposes a new algorithm that applies fuzzy logic to the results of gradient and zero crossing edge detection on an image to more accurately identify edges. The algorithm calculates gradient and zero crossings, applies fuzzy rules to classify pixels, and thresholds to determine final edge pixels.

1. Edge Detection
Presented By
Ishraq Fatafta

2. Agenda
O What is an edge.
O What is edge detection
O Usage of edge detection.
O Type of edges.
O Background.
O Edge detection methods
O Gradient based methods.
O Zero Crossing based.
O Proposed Algorithm.

3. Edges
O Abrupt change in the intensity of pixels.
O Discontinuity in image brightness or
contrast.
O Usually edges occur on the boundary of
two regions .

4. Edge Detection
O Process of identifying edges in
an image to be used as a
fundamental asset in image
analysis.
O Locating areas with strong
intensity contrasts.

5. Edge Detection Usage
O Reduce unnecessary information in the image
while preserving the structure of the image.
O Extract important features of an image
O Corners
O Lines
O Curves
O Recognize objects, boundaries, segmentation.
O Part of computer vision and recognition.

6. Edge Types
O Step Edge
O Ramp Edge
O Ridge
O Roof

7. Edge Detection Background
O Classical Gradient Edge detection.
O Sobel, Prewitt, Kirsch and Robinson.
O Gaussian based filters
O Marr and Hildreth.
O Canny
O Shunck, Witkin and Bergholm.
O Wavelets used for different scales.
O Heric and Zazula and Shih and Tseng.
O Fuzzy Logic and Neural Networks.

8. Edge Detection Steps
O Smoothing: Noise Reduction.
O Enhancement: Edge sharpening.
O Detection: Which to discard and which to
maintain.
O Thresholding.
O Localization: determine the exact location
of an edge.
O Edge thinning and linking are usually
required in this step.

9. Methods of Edge Detection
O Gradient methods (First Order Derivative)
O local maxima and minima using first
derivative in an image.
O Compute Gradient magnitude horizontally
and vertically.
O Zero-crossing methods (Second Order
Derivative)
O locate zeros in the second derivative of an
image.
O Laplacian of an Image.

10. Gradient based Edge
Detection
O Best used for abrupt discontinuities.
O Perform better in less noised images
O Magnitude of the gradient - strength
of the edge .
O Direction - opposite of the edge
direction.
Gy
G Gx 2
Gy 2
Gx Gy tan 1
Gx

11. Cont. Gradient based Edge
Detection
O Roberts Edge Detector.
O Prewitt Edge Detector.
O Sobel Edge Detector,
O Canny Edge Detector.

12. Cont. Gradient based Edge
Detection - Roberts
O 2X2 Convolution Mask
O Convolution Mask
O Gx Gy
1 0 0 -1
0 -1 1 0
O Differences are computed at the
interpolated points [i+1/2, j+1/2] and not
[i, j].
O Responds to edge with 450.

13. Cont. Gradient based Edge
Detection - Prewitt
O 3X3 Convolution Mask
O Convolution Mask
O Gx -1 0 1 Gy 1 1 1
-1 0 1 0 0 0
-1 0 1 -1 -1 -1
O The differences are calculated at the
center pixel of the mask.

14. Cont. Gradient based Edge
Detection - Sobel
O 3X3 Convolution Mask
O Convolution Mask
O Gx -1 0 1 Gy 1 2 1
-2 0 2 0 0 0
-1 0 1 -1 -2 -1
O The differences are calculated at the
center pixel of the mask.

15. Cont. Gradient based Edge
Detection
O Simple to implement
O Capable of detecting edges and their
direction
O Sensitive to noise
O Not accurate in locating edges

16. Cont. Gradient based Edge
Detection - Canny
O First derivative of a Gaussian filter will
approximately optimize the signal-to-noise
ratio and localization.

17. Cont. Gradient based Edge
Detection - Canny
O Three conditions for optimal detector
O Error rate: Respond to edges not noise.
O Localization: edges detected near true
edges.
O Response - Not identify multiple edge
pixels.

18. Cont. Gradient based Edge
Detection – Canny Algorithm
O
G Gx 2 Gy 2 Gx Gy

19. Cont. Gradient based Edge
Detection – Canny Algorithm
O Step 3
O Edge Direction
1 Gy
tan
Gx
O Step 4
O Resolve Edge Direction

20. Cont. Gradient based Edge
Detection – Canny Algorithm
O Step 5
O Non-maxima suppression: keep all local
maxima in the gradient and remove
everything else.
O Gives a thin line for edge
O Step 6
O Double / hysteresis thresholding

21. Cont. Gradient based Edge
Detection – Canny Algorithm
O Better localization
O Improved signal-to-noise ratio.
O Works fine under noisy conditions.
O Complex to implement and time
consuming.

22. Gradient based Edge

23. Zero Crossing based Edge
Detection
O Indicates the presence of a maxima.
O Pixel value passes through zero (changes its
sign).

24. Cont. Zero Crossing based
Edge Detection
O Laplacian of Gaussian
1 1 1
1 8 1
1 1 1
-1 2 -1
2 4 2
-1 2 -1

25. Cont. Zero Crossing based
Edge Detection - LOG
O Defined as:
O Greater the value of , broader is the
Gaussian filter, more is the smoothing

26. Cont. Zero Crossing based
Edge Detection - LOG
O Steps:
O Smoothing: Gaussian filter
O Enhance edges: Laplacian operator
O Zero crossings denote the edge location
O Use linear interpolation to determine the
sub-pixel location of the edge

27. Cont. Zero Crossing based
Edge Detection - LOG
O Computationally cheaper to implement
since we can combine the two filters into
one filter but it.
O Doesn’t provide information about the
direction of the edge.
O Probability of false and missing edges
remain.
O Localization is better than Gradient
Operators

28. Laplacian Of Gaussain

29. Proposed Algorithm
O Evaluate an Image using a Gradient filter.
O Evaluate an image using a Zero crossing
filter.
O Fuzzy Logic.

30. Cont. Proposed Algorithm
Fuzzy Logic
O Fuzzy Logic
O Problem-solving methodology.
O Draw definite conclusions from
vague, ambiguous or imprecise
information.
O Resembles human decision making with its
ability to work from approximate data and
find precise solutions.

31. Cont. Proposed Algorithm
Fuzzy Image Processing
O Collection of all approaches that
understand, represent and process the
images, their segments and features as
fuzzy sets.
O The representation and processing
depend on the selected fuzzy technique
and on the problem to be solved.

32. Cont. Proposed Algorithm
Fuzzy Image Processing

33. Cont. Proposed Algorithm
O Step 1
O Calculate gradient of an image using Sobel
filter.
O Step 2
O Calculate zero crossing using three
different values of standard deviation σ in
gausian of laplacian.
O Step 3
O Apply fuzzy rules on the two steps above.

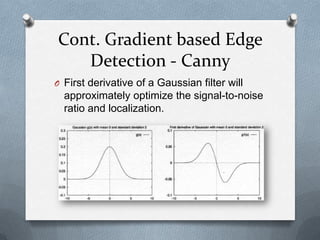
34. Cont. Proposed Algorithm
Step 1 - Sobel
O The resulted Gradient are mapped from
[0-255]
O Divide into four regions:
O Low class GL from [0-GL].
O Medium class GM
O from [GL-GM] .
O From [GM-GH] .
O High class GH from [GH-255].

35. Cont. Proposed Algorithm
Step 1 - Sobel

36. Cont. Proposed Algorithm
Step 2 - LOG
O

37. Cont. Proposed Algorithm
Step 2 - LOG
O Subtract three results.
O Apply an
algorithm.

38. Cont. Proposed Algorithm
Step 3 – Fuzzy sets
O Pixel (PG), zero crossing value (PZ), and
probability of a pixel corresponds to an edge
{EL, EM, EH}.
O If PG is in GL and PZ equals to 1, then P belongs to EL.
O If PG is in GL and PZ equals to a zero, then P belongs to EL.
O If PG is in [GL-GM] and PZ equals to 1, then P belongs to EM.
O If PG is in [GL-GM] and PZ equals to zero, then P belongs to
EL.
O If PG is in [GM-GH] and PZ equals to 1, then P belongs to EH.
O If PG is in [GM-GH] and PZ equals to zero, then P belongs to
EM.
O If PG is in GH and PZ equals to 1, then P belongs to EH.
O If PG is in GH and PZ equals to zero, then P belongs to EM.

39. Cont. Proposed Algorithm
Result
O All pixels in the EH will be considered as
an edge.
O All pixels in the EL will be discarded.
O All pixels in the EM, the gradient value will
be evaluated against a threshold value in
order to discard any pixel with value (0)
that may result from false zero crossing.