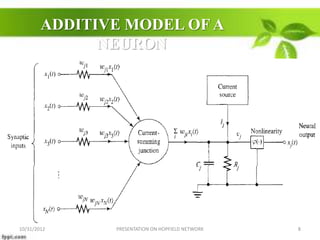
This document presents information on Hopfield networks through a slideshow presentation. It begins with an introduction to Hopfield networks, describing them as fully connected, single layer neural networks that can perform pattern recognition. It then discusses the properties of Hopfield networks, including their symmetric weights and binary neuron outputs. The document proceeds to provide derivations of the Hopfield network model based on an additive neuron model. It concludes by discussing applications of Hopfield networks.






















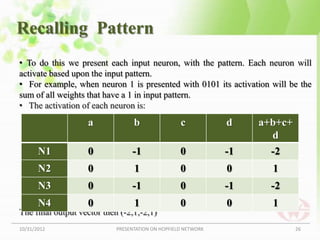
![Calculating The Weight Matrix
• And the matrix is:
Step 3: Set the Northwest diagonal to zero
• The reason behind this is, in Hopfield networks do not have their neurons
connected to themselves.
• So positions [1][1], [2][2], [3][3] and [4][4] in our two dimensional array
or matrix, get set to zero. This results in the weight matrix for the bit pattern
0101.
10/31/2012 PRESENTATION ON HOPFIELD NETWORK 25](https://image.slidesharecdn.com/ankita-copy-121101014346-phpapp02/85/HOPFIELD-NETWORK-25-320.jpg)