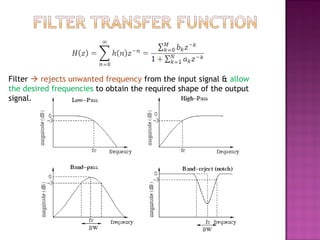
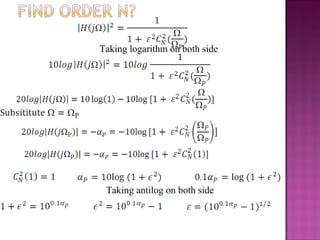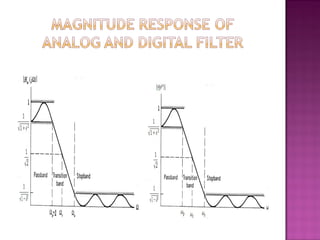
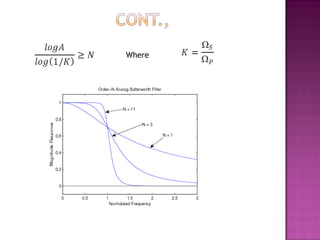
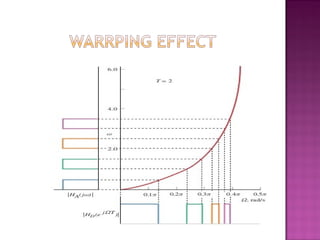
1. The document discusses and compares analog and digital filters. Digital filters are described as processing digital data/signals using elements like adders and multipliers, while analog filters use electronic components. 2. It also summarizes different types of common digital filters like Butterworth and Chebyshev filters. Butterworth filters have a monotonic magnitude response while Chebyshev filters exhibit ripple in the passband or stopband. 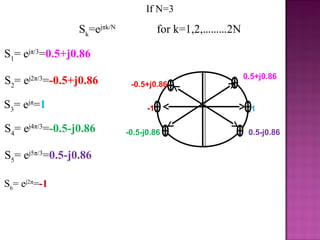3. The document outlines different methods to convert analog filters to digital filters, including bilinear transformation which maps the s-plane jΩ axis to the unit circle in the z-plane to avoid aliasing.

1. Prepared by
V.Thamizharasan
Assistant professor
Department of ECE
Erode Sengunthar Engineering College

2.  IIR Filter:
Recursive type  present output sample
depends on the present input & past input
and output sample.
FIR Filter:
Non Recursive type present output sample
depends on the present input & previous
input sample.
Impulse response: Realizable when
h(n)=0 for n≤0
Stability:

3. Filter  rejects unwanted frequency from the input signal & allow
the desired frequencies to obtain the required shape of the output
signal.

4.  Map the desired digital filter specification
into those for an equivalent analog filter.
 Derive analog transfer function for the
analog proto type
 Transform the analog transfer function into
digital transfer function.

7. S. No. Analog filter Digital filter
1 Processes analog inputs and
produce analog outputs
Processes and generate digital
data/signal.
2. Constructed by active/passive
electronic components
It consist of elements like adder,
multiplier and delay unit
3. It described by differential
equation
It described by difference
equation.
4. Frequency response can be
modified by changing the
components
Frequency response can be
modified by changing the filter
co-efficient

8. Advantages:
 Not influenced by component ageing, temperature &
power supply variations
 Highly immune to noise.
 Varity of shapes for the amplitude and phase
response.
 Does not occur impedance matching prblem.
 Operate wide range of frequency
 Altered the co-efficient at any time ,obtain the
desired response.
 Multiple filtering is also possible in digital filtering.
Disadvantages:
Quantization errors occur.

9.  Magnitude function of Butterworth filter is
N-order of the filter,
Ωc-cut off frequency.
Magnitude square function of normalized butterworth filter
Ωc = 1 rad/sec.
Substitude s=jΩ

10. Substitute s=jΩ
Find the poles location by put denominator =0
1+(-S2
)N
=0
If N=odd if N=even
(-S2
)N
=-S2N
(-S2
)N
=S2N
Therefore
1-S2N
=0 1+S2N
=0
S2N
=1 S2N
=-1
S2N
=ej2π
S2N
=e-j2π
S=ej2π/2N
S=e-j2π/2N
Sk
=ejπk/N
Sk
=ejπ(2k-1)/N

11. If N=3
Sk
=ejπk/N
for k=1,2,………2N
S1
= ejπ/3
=0.5+j0.86
S2
= ej2π/3
=-0.5+j0.86
S3
= ejπ
=1
S4
= ej4π/3
=-0.5-j0.86
S5
= ej5π/3
=0.5-j0.86
S6
= ej2π
=-1
1-1
-0.5+j0.86
0.5+j0.86
-0.5-j0.86 0.5-j0.86

12. Consider N=4
Dr=(s-s1
)(s-s2
) (s-s3
) (s-s4
)…..
Dr=(s+0.3826-j0.9238).(s+0.9238-j0.3826).
(s+0.9238-j0.3826) (s+0.3826+j0.9238)
Where
Stability :
considering only the poles that lie in the left half of the s-plane.
Dr=(s-s1
)(s-s2
) (s-s3
) (s-s4
)…..
Dr=(s+1)(s+0.5-j0.86)(s+0.5+j0.86) =(S+1)( S2
+S+1)

13. Order (N) Denominator of H(S)
1 (S+1)
2 (S2
+√2 S+1)
3 (S+1)( S2
+S+1)
4 (S2
+0.765 S+1) (S2
+1.847S+1)
5 (S+1)( S2
+0.618 S+1) (S2
+1.618S+1)
6 ( S2
+1.93185S+1) (S2
+√2S+1) (S2
+0.518S+1)
7 (S+1)( S2
+1.809S+1) (S2
+1.247S+1) (S2
+0.44S+1)

14. Magnitude function can be return as
Taking logarithm on both side

15. Taking antilog on both side

16. Take logarithm for above equation and then find N.
Where

17. Where

20.  Contains both poles & zeros
 Exhibits a monotonic behavior in the pass
band
 Equiripple behavior in the stop band.

21. Magnitude square response of Nth
order type-I filter is
εparameter related to ripple in pass band
CN
(x)=cos(N cos-1
x), |x|≤1  pass band.
CN
(x)=cosh(N cosh-1
x), |x|≤1  stop band.
Chebyshev polynomial is
CN
(x)=2xCN-1
(x)- CN-2
(x),N>1
Where C0
(x)=1 & C1
(x)=x

22. N=odd N=even
CN(x) - CN(-x) CN(-x)
CN(0) 0 (-1)N/2
CN(1) 1 1
CN(-1) -1 1
1.
2. CN
(x) Oscillates with equal ripple between ±1 for |x|≤1
3.For all N 0≤| CN
(x)|≤1 for 0≤|x|≤1
| CN
(x)|>1 for |x|≥1
4. CN
(x)is monotonically increasing for |x|>1 for all N.

24. Taking logarithm on both side
Taking antilog on both side

25. Substitute ε value

27. Equate Denominator is to zero & substitute s=jΩ

28. Equating real and imaginary part
Since cosh(Nϴ)>0 for ϴ real, then satisfying above equation only
Φ=(2k-1)π/2N for k=1,2,…………N
Find ϴ from above equation

29. For simplification
We know that

30. Where
Similarly

31. for k=1,2,….N

33. s.
No.
Parameter Butterworth Filter Chebyshev Filter
1 Magnitude
Response
Decrease monotonically
as frequency Ω increases
from 0 to ∞
It exhibits ripple in the
pass band or stop band
according to the type
2 Transmission
band
More Less
3. Poles •Lies on the circle
•No. of poles are more
•Lies on the ellipse
•No. of poles are less
4 Order Order of the filter is
more
Order of the filter is less

34. s.
No.
Transformati
on (or)
conversion
Equation
1 LPF to LPF S S / ΩC
2 LPF to HPF S ΩC/S
3. LPF to BPF
4 LPF to BSF

35. Methods:
1. Approximation of derivatives.
2. Bilinear Transformation
3. Impulse invariant transformation
4. Matched z-transformation
Converting analog filter into digital filter
Steps:
1.The jΩ axis in the s-plane should map into the unit circle in the z-plane.
Thus there will be direct relationship between the two frequency
variables in the two domains.
1.The left half of the s-plane should map into the inside of the unit circle
in the z-plane.
Thus a stable analog filter will be converted to stable digital
filter.

36. The z-transform of an infinite impulse response is
Mapping points from the s-plane to the z-plane
Substitute S=σ+jΩ
Express the complex variable Z in polar from as
Which gives 
 magnitude

38. Im(z)
Re(z)
Z-plane
S-
plane
j
Ω
σ
1.Any pole on jΩ axis
σ=0  then

39. 2. σ<0

40. Im(z)
Re(z)
Z-plane
S-plane
jΩ
σ
3. σ>0 

42.  Infinite no.of s plane poles  map to the
same location in the z-plane.
 They must have same real parts and
imaginary parts. differs by some integer
multiple of 2π/T.
 Cause aliasing when sampling of analog
signal.
 They analog poles will not be aliased by the
impulse invariant mapping if they are
confined to the s-plane “primary strip”(with
in π/T of the real axis)

43. Pk
poles
Ck
co-efficient
The inverse Laplace transform Ha
(s) is
We know

44. 
Due to the presence of aliasing ,the impulse invariant
method is appropriate for the design of low pass &
bandpass filter.
It is not suitable for HIGH pass filter.

45.  It is conformal mapping
 Transforms the s-plane jΩ axis poles into the
unit circle in the z-plane
 Mapping is only once
 Avoid aliasing of frequency components.
 All s-plane LHP poles are mapped into inside
of the unit circle in the z-plane
 All s-plane RHP poles are mapped into
outside of unit circle in the z-plane

46. Warping effect
Low frequency  w & Ω have linear relation ship
High frequency  w & Ω does not have linear relation ship