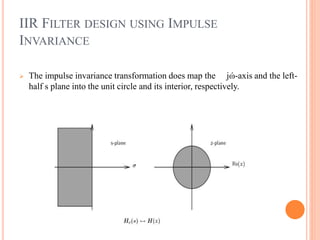
This document discusses digital filter design methods. It introduces IIR and FIR filters and their design techniques. The key methods covered are: 1. IIR filter design using impulse invariance, which samples the impulse response of an analog filter to obtain the discrete-time filter. 2. IIR filter design using bilinear transformation, which maps the continuous s-domain to the discrete z-domain to avoid aliasing. 3. FIR filter design using frequency sampling, which designs a linear phase FIR filter by sampling the desired frequency response and taking the inverse DFT.

1. DIGITAL SIGNAL
PROCESSING(2171003)
SUBJECT: FILTER DESIGN
PREPARED BY:
NAIMISH PATEL(140053111017)

2. OUTLINE
 Introduction.
 IIR Filter Design by Impulse invariance method.
 IIR Filter Design by Bilinear transformation method.
 FIR Filter Design by Frequency sampling technique.
 Advantages and Disadvantages.

3. INTRODUCTION
 Filter:- The system that modify the spectral contents of the input
signal are termed as filter.
 Filters mainly are of two types
1-Analog Filter
2-Digital Filter
Filter
Analog Filter
Digital Filter
IIR Filter
FIR Filter

4. ADVANTAGES OF DIGITAL FILTER
 Performance of digital filter can not influenced due to component
ageing, temp, &power supply variations
 Highly immune to noise.
 Operated over wide range of frequency.
 Multiple filtering possible only in digital filter.

5. INTRODUCTION
 Now we will introduce to the design method of the FIR filter and IIR
filter respectively.
 IIR is the infinite impulse response abbreviation.
 Digital filters by the accumulator, the multiplier, and it constitutes
IIR filter the way, generally may divide into three kinds, respectively
is Direct form, Cascade form, and Parallel form.
 IIR filter design methods include the impulse invariance, bilinear
transformation.

6. INTRODUCTION
 FIR is the finite impulse response abbreviation, because its design
construction has not returned to the part which gives.
 Its construction generally uses Direct form and Cascade form.
 FIR filter design methods include the window function, frequency
sampling.

7. IIR FILTER DESIGN USING IMPULSE
INVARIANCE
Steps:
s z transformation
Step 1: let the impulse response of analog filter is h(t)
Given the transfer function in S-domain, find the impulse response h(t).
Step 2: Sample h(t) to get h(n).
unit sample response can be obtained by putting t=nT
Step 3: Find H(Z), by taking z-transform of h(n).

8. IIR FILTER DESIGN USING IMPULSE
INVARIANCE
 The most straightforward of these is the impulse invariance
transformation
 Let h(t) be the impulse response corresponding to H(s), and define
the continuous to discrete time transformation by setting h(n)=h(nT)
 We sample the continuous time impulse response to produce the
discrete time filter

9. IIR FILTER DESIGN USING IMPULSE
INVARIANCE
 The impulse invariance transformation does map the jώ-axis and the left-
half s plane into the unit circle and its interior, respectively.

10. IIR FILTER DESIGN BY BILINEAR
TRANSFORMATION METHOD
 The most generally useful is the bilinear transformation.
 To avoid aliasing of the frequency response as encountered with the
impulse invariance transformation.
 We need a one-to-one mapping from the s plane to the z plane.
 The problem with the transformation is many-to-one.'s T
z e

11. IIR FILTER DESIGN BY BILINEAR
TRANSFORMATION METHOD
 We could first use a one-to-one transformation from s to s’ , which
compresses the entire s plane into the strip
 Then s’ could be transformed to z by
with no effect from aliasing.
Im( ')s
T T
 
  
's T
z e

12. IIR FILTER DESIGN BY BILINEAR
TRANSFORMATION METHOD
 The transformation from s to s’ is given by

 The characteristic of this transformation is seen most readily from
its effect on the jώ axis. Substituting s=jώ and s’= jώ’ , we obtain
12
' tanh ( )
2
sT
s
T


12
' tan ( )
2
T
T

 


13. IIR FILTER DESIGN BY BILINEAR
TRANSFORMATION METHOD
 The discrete-time filter design is obtained from the continuous-time
design by means of the bilinear transformation
1 1
(2/ )(1 )/(1 )
( ) ( ) |c s T z z
H z H s  
  


14. FIR FILTER DESIGN BY FREQUENCY
SAMPLING TECHNIQUE
 We wish to derive a linear phase IIR filter with real nonzero h(n) .
The impulse response must be symmetric
where are real and denotes the integer part
[ /2]
0
1
2 ( 1/ 2)
( ) 2 cos( )
1
M
k
k
k n
h n A A
M



 


kA [ / 2]M

15. FIR FILTER DESIGN BY FREQUENCY
SAMPLING TECHNIQUE
 It can be rewritten as
 where N=M+1 and
Therefore, it may write
where
1
/ 2 /
0
/2
( )
N
j k N j kn N
k
k
k N
h n A e e 



 
k N kA A 
1
0
/2
( ) ( )
N
k
k
k N
h n h n



 
/ 2 /
( ) j k N j kn N
k kh n A e e 


16. FIR FILTER DESIGN BY FREQUENCY
SAMPLING TECHNIQUE
 with corresponding transform
where
 Hence
which has a linear phase
1
0
/2
( ) ( )
N
k
k
k N
H z H z



 
/
2 / 1
(1 )
( )
1
j k N N
k
k j k N
A e z
H z
e z







' ( 1)/2 sin / 2
( )
sin[( / / 2)]
j T N
k k
TN
H A e
k N T
 

 
 



17. FIR ADVANTAGES AND DISADVANTAGE
 FIR advantage:
1. Finite impulse response
2. It is easy to optimalize
3. Linear phase
4. Stable
 FIR disadvantage:
1. It is hard to implementation than IIR

18. IIR ADVANTAGE AND DISADVANTAGES
 IIR advantage :
1. It is easy to design
2. It is easy to implementation
 IIR disadvantage:
1. Infinite impulse response
2. It is hard to optimalize than FIR
3. Non-stable

19. THANK YOU