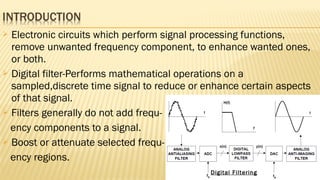
This document discusses digital filters. It begins by defining digital filters as electronic circuits that perform signal processing functions by removing or enhancing certain frequency components of a sampled, discrete-time signal. It then outlines four basic types of ideal digital filters defined by their magnitude responses. The document also discusses different classifications of digital filters based on characteristics like linearity, time-invariance, and structure. It provides examples of common filter structures like direct form, cascade form, and parallel form. Finally, it briefly compares digital and analog filters, noting advantages and disadvantages of each.

1. Department of Microelectronics,
Indian Institute of Information Technology, Allahabad
SUBMITTED BY:
Prashant singh(imi2011003)
Rahul Patidar(imi2011011)

2.  Introduction
 Classification
 Types
 Structures
 Digital Vs Analog filters
 Refrences

3.  Electronic circuits which perform signal processing functions,
remove unwanted frequency component, to enhance wanted ones,
or both.
 Digital filter-Performs mathematical operations on a
sampled,discrete time signal to reduce or enhance certain aspects
of that signal.
 Filters generally do not add frequ-
ency components to a signal.
 Boost or attenuate selected frequ-
ency regions.
Digital Filtering

4.  Magnitude response consideration.
 Four basic types of ideal filters with magnitude responses as shown
below
π
1
ω
0 ωc–ωc
HLP(e jω
)
− π π
ω
0 ωc–ωc
1
HHP (e jω
)
− π
π− π
ω
11–
–ωc1 ωc1–ωc2 ωc2
HBP (e jω)
− π π
ω
1
–ωc1 ωc1–ωc2 ωc2
HBS(e jω
)

5.  Depending on the form of the filter equation
(a) Linear filters versus nonlinear filters.
(b) Time-invariant filters versus time-varying filters.
(c) Adaptive filters versus non-adaptive filters.
(d) Recursive versus non-recursive filters.
 Depending on the structure of implementation
(a) Direct-form, cascade-form, parallel-form and lattice structures.

6.  A class of linear filters whose behavior does not change over time
- Linearity implies that the filter meets the scaling and superposition properties.
 Two types
1.FIR filter
-Operate only on previous values of the input
2.IIR filter
-Operates on previous values of input & output both

7.  A recursive filter has feedback from
output to input, and in general
its output is a function of the previous
output samples and the present and
past input samples

8.  A non recursive filter has no feedback from output to input, and
in general its output is a function of the present and past input
samples

9.  Direct Form
Direct Filter Structure

10.  Cascade Form
Cascade Filter Structure

11.  Parallel Form
Parallel Form Structure

12. DIGITAL
High Accuracy
Linear Phase (FIR Filters)
Flexible, Adaptive Filtering
Possible
Easy to Simulate and Design
Computation Must be Completed
in
Sampling Period - Limits Real
Time Operation
Requires High Performance
ADC,DAC & DSP
ANALOG
Less Accuracy–Component Tolerances
Non-Linear Phase
Adaptive Filters Difficult
Difficult to Simulate and
Design
Analog Filters Required at High
Frequencies and for Anti-
Aliasing Filters
No ADC, DAC, or DSP Required

13.  Introduction to Speech Processing | Ricardo Gutierrez-Osuna | CSE@TAMU, chapter 10 of [Taylor, TTS synthesis, 2009].
 An Introduction to Digital Filters,application note,january1999, Intersil and Design is a trademark of Intersil Corporation. |
Copyright©Intersil Corporation 2000
 Digital Filters and Z Transforms,Copyright © Richard C. Bailey and David M. Harrison, 1998, 1999
 http://en.wikipedia.org/wiki/Digital_filter