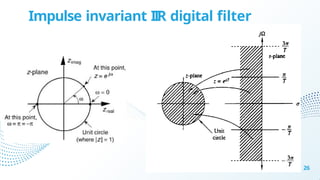
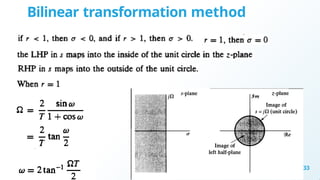
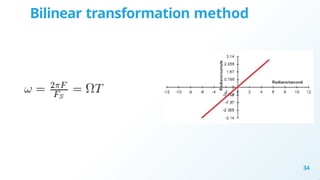
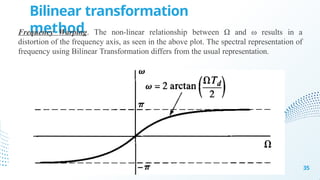
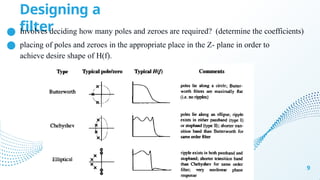
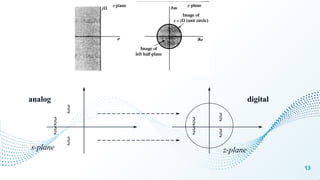
Chapter 4 discusses filter design techniques, including definitions, types, and terminologies of filters, particularly focusing on digital filters. It highlights the advantages of digital filters over analog filters, including reprogrammability and stability, and details the design methods for Infinite Impulse Response (IIR) and Finite Impulse Response (FIR) filters. The chapter further elaborates on techniques such as approximations of derivatives, impulse invariance, and bilinear transformation for designing IIR filters from analog counterparts.

1. Chapter - 4
Filter design
techniques

2. Outlines
2
● Filter definition
● Types of filter
● Filter terminologies
● Digital filters

3. What is filtering ?
● It is a process of selectively removing or altering parts of
frequency content of original signal to create a new signal.
● EX : for audio system
bass – reduce high frequency
treble – reduce low frequency
3

4. Types of filters
4

5. Filter Response
5

6. Filter terminologies
6

7. Filter terminologies
7

8. Digital filters
8
● Digital filters operates on the discrete time signal
● Advantages over analog filters:
1) their characteristics are truly time invariant (like
temperature changing, components)
2) filter behavior can be changed by reprogramming
● Two types of digital filters
3) IIR (Infinite Impulse Response)
4) FIR (Fifinite Impulse Response), referring to the length of
h(n).

9. Designing a
filter
9
● Involves deciding how many poles and zeroes are required? (determine the coefficients)
● placing of poles and zeroes in the appropriate place in the Z- plane in order to
achieve desire shape of H(f).

10. Comparison between IIR and FIR
filters
10
Parameter/characteristic IIR filter FIR filter
Unit sample response h(n) infinite duration finite duration
Poles and zeroes both are present, sometimes
all pole filter
All zeros filter
Recursive/ no recursive
(feedback from o/p)
Use feedback, recursive Do not use feedback, non recursive
stability Not always Inherently stable
Number of multiplication,
memory requirement
less more
Order of the filter for
similar specification
Lower order Higher order
Phase characteristic Non linear phase response Linear phase response
Analytical design More closer results (one
time implementation)
Iterative process (result not necessarily
similar to analytical)

11. Design of IIR filter from analog
filters
● Methods of IIR filter designing
1) Approximations of derivatives
2) Impulse invariance
3) Bilinear transformation
● Steps of designing
4) Ha(s) - response in s plan available
5) ha(t) - from that find impulse response of analog form
6) ha(nT) – h(n) - convert ha(t) to h(n) discrete sample response
by
sampling 11

12. Stability criteria for analog and digital
domain
12
● In analog domain stable system : if all its poles lie in the left half of the
s- plan
● So conversion required:
1)the jΩ axis in the s-plan should map into the unit circle in the z-plan.
Thus there will be a direct relationship between the two frequency variables in
the two domains
2)the left half plan (LHP) of the s-plan should map into the inside of
the unit circle in the z –plan. Thus a stable analog filter will be converted
to a stable digital filter

13. s-plane z-plane

13







analog digital

14. IIR filter design by
Approximations of
derivatives
14

15. IIR filter design by Approximations of derivatives
● Simplest method for converting an analog filter into a digital filter.
● Concept : which approximate the differential equation(analog domain)
by
an equivalent difference equation(digital domain).
● For the derivative dy(t)/dt at a time t = nT we substitute the
backward difference [y[n]-y[n-1]]/T.
15
d y
( t )
dt

y ( n )  y ( n  1 )
T
t  n T
Where T represents the sampling interval and y(n) = y(nT).

16. IIR filter design by Approximations of derivatives
● analogue differentiator with output dy(t)/dt has the system function H(s) = s
● digital system that produces the output [y(n)-y(n-1)]/T has the system function
H(z) = (1 – z-1)/T
● S to z
domain
● The second derivative d2y(t)/dt2 is replaced by the second difference which is
given by
16
1  z1
s 
T
T 2
dt 2
d2
y(t)

y(n)  2y(n  1)  y(n  2)
T
T2




 

s2

1  2z1
 z2
 1  z1

2

17. IIR filter design by Approximations of derivatives
● generalize from
● Now from equation
 If we substitute s = jΩ in above equation, we
have
17
T
s k 




 1  z  1

k
1  z1
s 
T
1
1  s T
we have Z equals to z 
z 
1 jT
1

18. IIR filter design by Approximations of derivatives
● plan to z plan conversion
● The mapping takes points in the LHP of s into corresponding points
inside this circle and the points in RHP plane in
s are mapped into points outside this circle.
18

19. IIR filter design by Approximations of derivatives
19
● Advantage : This mapping has the desirable property that a stable analog
filter is Transformed into a stable digital filter.
● Disadvantage: However, the possible location of the poles of the digital
filter are confined to relatively small frequencies and, thus, the
mapping is restricted to low-pass and band-pass filters having relatively
small resonant frequencies.

20. IIR filter design by
20
Impulse Invariance
method

21. Impulse invariant IIR digital filter
● How to transform s to z plan
● System function Ha(s) can be expressed in partial fraction
expansion
form if poles are distinct
● Pk are poles , Ck- partial fraction coefficient
● Now using inverse Laplace transform

22. Impulse invariant IIR digital
filter
● Now unit sample response by sampling
● Now system function can be obtained by taking z-
transform
● Equating H(s) and H(z)

23. Impulse invariant IIR digital
filter
23
● S- plan to z-plan conversion
Analog filter has poles at s = pk

24. Impulse invariant IIR digital filter
 Entire jΩ axis mapped on the unit circle. Hence the mapping
is not one to one.
 The range of
 Hence the corresponding range of ‘Ω’ is, where
24

25.  Thus mapping of jΩ axis many a times in a unit circle.
Impulse invariant IIR digital filter
25

26. Impulse invariant IIR digital filter
26

27. ● Advantage: Relationship between continuous time and discrete
time frequency is linear; except for aliasing the shape of the
frequency response is preserved.
● Disadvantage: Method is useful only for low pass and band pass
filter at low frequency.
27
Impulse invariant IIR digital filter

28. Bilinear
transformation
method

29. ● Principal: Approximation of analog integration by trapezoidal formula in
digital domain
● Suppose that x(t) is the input and y(t) the output of an integrator with transfer
function
● Sampling the input and the output of this filter using a sampling period Ts,
we see that the integral at time nTs is
● where y((n−1)Ts) is the integral at time (n−1)Ts. 29
Bilinear transformation
method

30. Bilinear transformation method
● If Ts is very small, the integral between (n−1)Ts and nTs can be
approximated by the area of a trapezoid with
bases x((n−1)Ts) and x(nTs) and height Ts
● This is called the trapezoidal rule
approximation of an integral
30

31. Bilinear transformation
method
31

32. Bilinear transformation
method
● S to z domain transfer

33. Bilinear transformation method
33

34. Bilinear transformation method
34

35. Bilinear transformation
method
35
Frequency Warping. The non-linear relationship between Ω and ω results in a
distortion of the frequency axis, as seen in the above plot. The spectral representation of
frequency using Bilinear Transformation differs from the usual representation.

36. 36

37. 37

38. 38

39. 39

40. 40

41. “
41