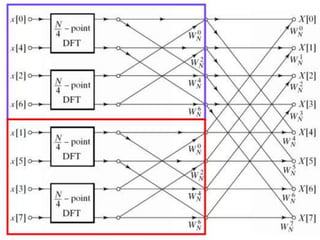
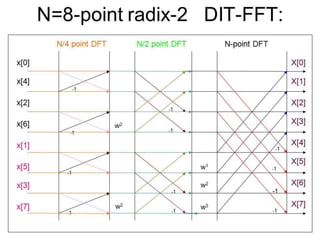
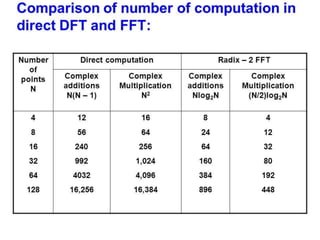
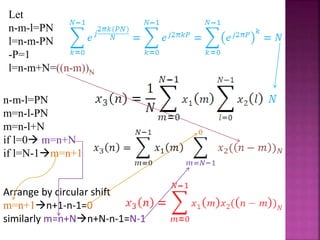
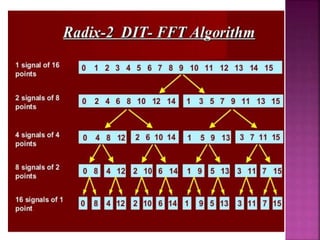
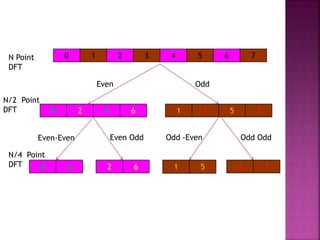
The document discusses the Fast Fourier Transform (FFT) algorithm. It explains that FFT reduces the number of computations needed to calculate the Discrete Fourier Transform (DFT) of a sequence by decomposing the DFT into successive DFTs of smaller sizes. Specifically, it breaks down the N point DFT into multiple N/2 point DFTs recursively until it reaches DFTs of size 1. This decomposition reduces the complexity from O(N^2) for DFT to O(NlogN) for FFT.

1. Prepared by
V.Thamizharasan
Assistant professor
Department of ECE
Erode Sengunthar Engineering College

2. X(k+N)=X(k) for all k
Formula for DFT
X(k+N)=X(k)

3. x(n+N)=x(n) for all n
Formula for IDFT

4. If two finite duration sequence x1(n) & x2(n) are linearly
combined as
The DFT of x3(n)
is

5. The shifted version of x(n) is
Same Way
DFT{x(n)}=x(k)

6. N-m+n=l if n=0 then l=N-m
n=l+m-N if n=m-1 then l=N-m+m-1=N-1
Consider 1st part
1
2

7. Consider 2nd part
N-m+n=l if n=m then l=N
n=l+m-N if n=N-1 then l=N-m+N-1=2N-m-1
3

8. Add 1st and 2nd part of equation 2 & 3

9. N-n=m if n=0 then m=N
N-M=n if n=N-1 then m=1

11. Similarly

12. If two finite duration sequence x1(n) & x2(n) are finite duration
Sequence both of length N with DFTs X1(K)& X2(K)
Now we find x3(n) for which the DFT is X3(K) Where
Similarly
N

14. Let
n-m-l=PN
l=n-m-PN
-P=1
l=n-m+N=((n-m))N
n-m-l=PN
m=n-l-PN
m=n-l+N
if l=0 m=n+N
if l=N-1m=n+1
Arrange by circular shift
m=n+1n+1-n-1=0
similarly m=n+Nn+N-n-1=N-1

15. N

17. DFT used to perform linear filtering
FFT Set of Algorithms, proposed by
Cooly and Tukey 1965
FFT: computing DFT with less number of
computation than direct evaluation of DFT.
FFT used in digital spectral analysis,
filter simulation, auto correlation & pattern
recognition.
FFT reduce the computation time
Performance improved compared to DFT.

18. Evaluate one value of K No.of complex Multiplication N.
All the N value of X(k) 
No.of Complex Multiplication is N*N=N2
No.of Addition
one value of k: (N-1) Addition
For N value of k: N(N-1)

19. =
No.of multiplication
Computation of X(k) for each K Requires
4N (each Summation N multiplication) Real Multiplication
X(k) for all k from 0 to N-1 N(4N)=4 N2 Real Multiplication
No.of Addition:
Each of 4 summation of N terms
Requires N-1 Real two input addition4(N-1)
Combine the Sum to Get the real part & imaginary part 2
For one k value  4(N-1)+ 2=4N-2
For all the value of K N*(4N-2)

20. Fast Fourier Transform
FFT  applicable for two basic properties for twiddle
factor
It reduces the no.of complex multiplication
Basic Principle of FFT
Decomposing the computation of Discrete Fourier
transform of sequence of length N into successively smaller
discrete FTs
Types of FFT
1. Decimation in Time [DIT]
2. Decimation Frequency [DIF]

21.  The sequence for which we need the DFT is
successively divided into smaller sequence &
DFTs of these subsequence are combined in a
certain pattern to obtain the required DFT of the
entire sequence.
 It also known as Radix-2 DIT FFT Algorithm.
The No.of output points N can be expressed as a
power 2 that is N= 2M, M Integer

23. 0 1 2 3 4 5 6 7
0 2 4 6 1 3 5 7
0 4 2 6 1 5 3 7
N Point
DFT
N/2 Point
DFT
N/4 Point
DFT
Even Odd
Even-Even Even Odd Odd -Even Odd Odd

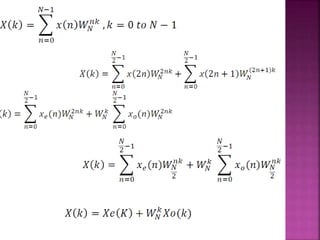
26. -1
-1
-1
-1
WN
0
WN
1
WN
2
WN
3
x[7]
x[5]
x[3]
x[1]
x[6]
x[4]
x[2]
x[0]
H[2]
H[3]
H[1]
H[0]
G[3]
G[2]
G[1]
G[0]
X[0]
X[1]
X[2]
X[3]
X[4]
X[5]
X[6]
X[7]
N/2 POINT
DFT
N/2 POINT
DFT
Figure 9.3