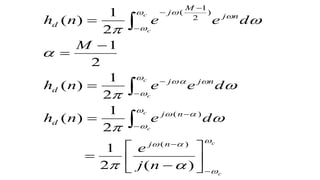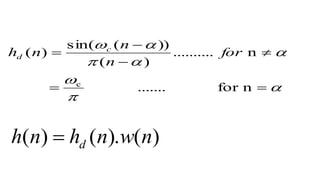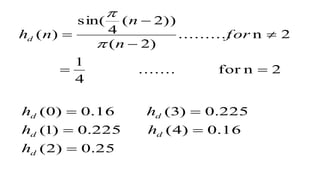This document discusses the design of FIR filters using window functions. It begins by explaining that windows are used to modify the impulse response of filters to reduce ripples and achieve a smooth transition from passband to stopband. It then provides examples of common window functions, including rectangular, Hanning, Hamming, and Blackman windows. It concludes by showing the design of a low-pass FIR filter using a Hamming window to meet specific specifications for cutoff frequency and transition width.

1. FIR filter design using windows
- SARANG JOSHI

2. Windows
• Windows are the finite duration sequences used to modify
the impulse response of filters in order to reduce ripples in
passband and stopband and to achieve desired transition
from passband to stopband.
• The infinite duration impulse response can be converted to a
finite duration impulse response by truncating the infinite
series.

3. But this results in undesirable oscillations in the passband and
stopband of digital filter which is due to the slow convergence of
Fourier series near the points of discontinuity.
These undesirable oscillations can be reduced by using a set of
time-limited weighting functions, w(n), referred to as window
functions , to modify fourier coefficients

4. 1 Rectangular Window
1),-(M|n|for0
1),-(M|n|for1
)(rect)(W Nrec





 nn
M is the length of window

5. 2.Hanning window
otherwise.0
1,-M0,1,2...n)),-cos((1
n)( 1-M
n2
2
1
Han


 


w

6. 3.Hamming window
otherwise.0
1-M0,1,2.....)cos(0.46-0.54
)(
1
n2
Ham


 
 
n
n
M
w


7. 4.Blackman window
otherwise.0
1-M0,1,2.....)0.08cos()cos(0.5-0.42
)(
1
n4
1
n2
Bla


 
 
n
n
MM
w


8. 





deHnh
eH
nj
dd
c
M
j
d
c
c





)(
2
1
)(
||0.............{)(
)
2
1
(
Desired frequency response for Low pass FIR filter
M is the length of filter
Desired impulse response for Low pass FIR filter

9. c
c
c
c
c
c
c
c
nj
e
denh
deenh
M
deenh
nj
nj
d
njj
d
nj
M
j
d













































)(2
1
2
1
)(
2
1
)(
2
1
2
1
)(
)(
)(
)
2
1
(

10. 



























nfor.......
n..........
)(
))(sin(
)(
2
)sin(
)(2
1
c
)()(
for
n
n
nh
j
ee
nj
ee
c
d
jj
njnj cc

11. )().()( nwnhnh d











nfor.......
n..........
)(
))(sin(
)(
c
for
n
n
nh c
d

12. Q. Design a LPF using hamming window to
meet following specifications
4
||0.............{)( 2 
 
  j
d eH











nfor.......
n..........
)(
))(sin(
)(
c
for
n
n
nh c
d
Solution :
2
1

M


13. 2nfor.......
4
1
2n..........
)2(
))2(
4
sin(
)(




 for
n
n
nhd


25.0)2(
16.0)4(225.0)1(
225.0)3(16.0)0(



d
dd
dd
h
hh
hh

14. otherwise.0
1-M0,1,2.....)cos(0.46-0.54
)(
1
n2
Ham


 
 
n
n
M
w

otherwise.0
0,1,2,3,4)cos(0.46-0.54
)(
4
n2
Ham


 

n
nw

otherwise.0
0,1,2,3,4)cos(0.46-0.54
)(
2
n
Ham


 

n
nw


15. 08.0)4(
54.0)3(
1)2(
0.54)1(
0.08)0(
Ham
Ham
Ham
Ham
Ham





w
w
w
w
w

16. 08.0)4(
54.0)3(
1)2(
0.54)1(
0.08)0(
Ham
Ham
Ham
Ham
Ham





w
w
w
w
w
16.0)4(
225.0)3(
25.0)2(
225.0)1(
16.0)0(





d
d
d
d
d
h
h
h
h
h
)().()( nwnhnh d

17. 0128.0)4(
1215.0)3(
25.0)2(
1215.0)1(
0128.0)0(





h
h
h
h
h
)1()( nMhnh 

18. RATE, FOLLOW & SHARE
https://unacademy.com/lesson/fir-filter-design-using-windows/TII60A0X

19. THANK YOU !