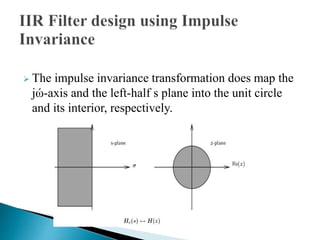
This document discusses different methods for designing digital filters, including FIR and IIR filters. It describes the impulse invariance and bilinear transformation methods for designing IIR filters, as well as frequency sampling techniques for FIR filter design. Advantages and disadvantages of FIR and IIR filters are provided. The key steps of the bilinear transformation method are outlined, along with discussions of designing linear phase IIR filters and specifying filters based on desired magnitude responses.

1. TOPIC:-FILTER DESIGN
By
Nehe Pradeepkumar
Dattatraya

2.  Introduction.
 IIR Filter Design by Impulse invariance method.
 IIR Filter Design by Bilinear transformation method.
 FIR Filter Design by Frequency sampling technique.
 Advantages and Disadvantages.

3.  Filter:- The systm that modify the spectral contents of the
input signal are termed as filter.
 Filters mainly are of two types
1-Analog Filter
2-Digital Filter
Filter
Analog Filter
Digital Filter
FIR Filter
IIR Filter

4.  Performance of digital filter can not influenced due to
component ageing, temp, &power supply variations
 Highly immune to noise.
 Operated over wide range of frequency.
 Multiple filtering possible only in digital filter.

5.  Now we will introduce to the design method of the
FIR filter and IIR filter respectively.
 IIR is the infinite impulse response abbreviation.
 Digital filters by the accumulator, the multiplier, and
it constitutes IIR filter the way, generally may divide
into three kinds, respectively is Direct form, Cascade
form, and Parallel form.
 IIR filter design methods include the impulse
invariance, bilinear transformation.

6.  FIR is the finite impulse response abbreviation,
because its design construction has not returned to the
part which gives.
 Its construction generally uses Direct form and
Cascade form.
 FIR filter design methods include the window
function, frequency sampling.

7. Steps:
s z transformation
Step 1: let the impulse response of analog filter is h(t)
Given the transfer function in S-domain, find the
impulse response h(t).
Step 2: Sample h(t) to get h(n).
unit sample response can be obtained by putting
t=nT
Step 3: Find H(Z), by taking z-transform of h(n).

8.  The most straightforward of these is the impulse
invariance transformation
 Let h(t) be the impulse response corresponding to
H(s), and define the continuous to discrete time
transformation by setting h(n)=h(nT)
We sample the continuous time impulse response to
produce the discrete time filter

9.  The impulse invariance transformation does map the
jώ-axis and the left-half s plane into the unit circle
and its interior, respectively.

10.  The most generally useful is the bilinear
transformation.
 To avoid aliasing of the frequency response as
encountered with the impulse invariance
transformation.
We need a one-to-one mapping from the s plane to
the z plane.
 The problem with the transformation is
many-to-one.
s 'T z  e

11. We could first use a one-to-one transformation from
s to s’ , which compresses the entire s plane into the
strip
 
  Im(s ')

T T
 Then s’ could be transformed to z by
with no effect from aliasing.
s 'T z  e

12.  The transformation from s to s’ is given by

1 2
sT
 
' tanh ( )
2
s
T
 The characteristic of this transformation is seen most
readily from its effect on the jώ axis. Substituting
s=jώ and s’= jώ’ , we obtain
1 2
T
' tan ( )
2
T

  

13.  The discrete-time filter design is obtained from the
continuous-time design by means of the bilinear
transformation
H ( z ) H ( s ) | c s  T  z  
z
 1 1 (2/ )(1 )/(1 )


14. ' ( ) d H 
 For arbitrary, non-classical specifications of , the
calculation of hn
() , n=0,1,…,M, via an appropriate
d approximation can be a substantial computation task.
 It may be preferable to employ a design technique
that utilizes specified values of H ' ( 
) directly,
d without the necessity of determining
() d hn

15. We wish to derive a linear phase IIR filter with real
nonzero h(n) . The impulse response must be
symmetric
M
[ /2]
k n
 
h n A A


( )  
2 cos( )
0

1
2 ( 1/ 2)
1
k
k
M
where are real and denotes the integer part
k A[ / 2] M

16.  It can be rewritten as

h n A e e  
 
 where N=M+1 and
Therefore, it may write

 
h n h n
( ) ( )
where
1
/ 2 /
0
/2
( )
N
j k N j kn N
k
k

k 
N
k N k A A 
1
0
/2
N
k
k

k 
N
/ 2 / ( ) j k N j kn N
k k h n A e e   

17.  with corresponding transform
N

 
H z H z
( ) ( )
where
 Hence
1
k
0
k N
/2
k


j 
k /
N N
A e z

(1 )
H z


k j k N
2 / 1
( )
k
1


e z

sin 
/ 2
' ( )
 ( 1)/2 which has a linear phase
sin[( / / 2)]
j T N
k k
TN
H A e
k N T

 
  


18.  The only nonzero contribution to H'(  ) at  
 is
k from , and hence that
'( ) k H  '( )k k H   N A
 Therefore, by specifying the DFT samples of the
desired magnitude response at the
H ' () 
d frequencies , and setting
k 
' ( ) / k d k A   H  N

19. We produce a filter design from equation for which
H '(k )  Hd' (k )
 The desired and actual magnitude responses are equal
at the N frequencies
k 

20.  In between these frequencies, is interpolated as
H '()
the sum of the responses , and its magnitude
does not, equal that of
' () k H 
' () d H 

21.  FIR advantage:
1. Finite impulse response
2. It is easy to optimalize
3. Linear phase
4. Stable
 FIR disadvantage:
1. It is hard to implementation than IIR

22.  IIR advantage :
1. It is easy to design
2. It is easy to implementation
 IIR disadvantage:
1. Infinite impulse response
2. It is hard to optimalize than FIR
3. Non-stable