The document discusses Fourier series and their application to functions defined over intervals. It defines the Fourier sine and cosine series for functions on [-L,L] by extending the functions to the full interval [-π,π] in an odd or even way. The Fourier sine series results from the odd extension, using sine terms, while the Fourier cosine series uses the even extension and cosine terms. Examples are provided of calculating the Fourier sine and cosine series for basic functions over [-1,1]. The approach generalizes to 2L-periodic functions defined on [-L,L].

1. TARUN GEHLOT (B.E, CIVIL HONORS)
Recall that the Fourier series of f(x) is defined by
where
We have the following result:
Theorem. Let f(x) be a function defined and integrable on interval .
(1)
If f(x) is even, then we have
and
(2)
If f(x) is odd, then we have
and

2. TARUN GEHLOT (B.E, CIVIL HONORS)
This Theorem helps define the Fourier series for functions defined only on the
interval . The main idea is to extend these functions to the interval and
then use the Fourier series definition.
Let f(x) be a function defined and integrableon . Set
and
Then f1 is odd and f2 is even. It is easy to check that these two functions are defined and
integrable on and are equal to f(x) on . The function f1 is called the odd
extension of f(x),
while f2 is called its even extension.
Definition. Let f(x), f1(x), and f2(x) be as defined above.
(1)
The Fourier series of f1(x) is called the Fourier Sine series of the function f(x),
and is given by
where

3. TARUN GEHLOT (B.E, CIVIL HONORS)
(2)
The Fourier series of f2(x) is called the Fourier Cosine series of the function f(x),
and is given by
where
Example. Find the Fourier Cosine series of f(x) = x for .
Answer. We have
and
Therefore, we have

4. TARUN GEHLOT (B.E, CIVIL HONORS)
Example. Find the Fourier Sine series of the function
Answer. We have
Hence
TARUN GEHLOT (B.E, CIVIL HONORS)
Find the Fourier Sine series of the function f(x) = 1 for .

5. TARUN GEHLOT (B.E, CIVIL HONORS)
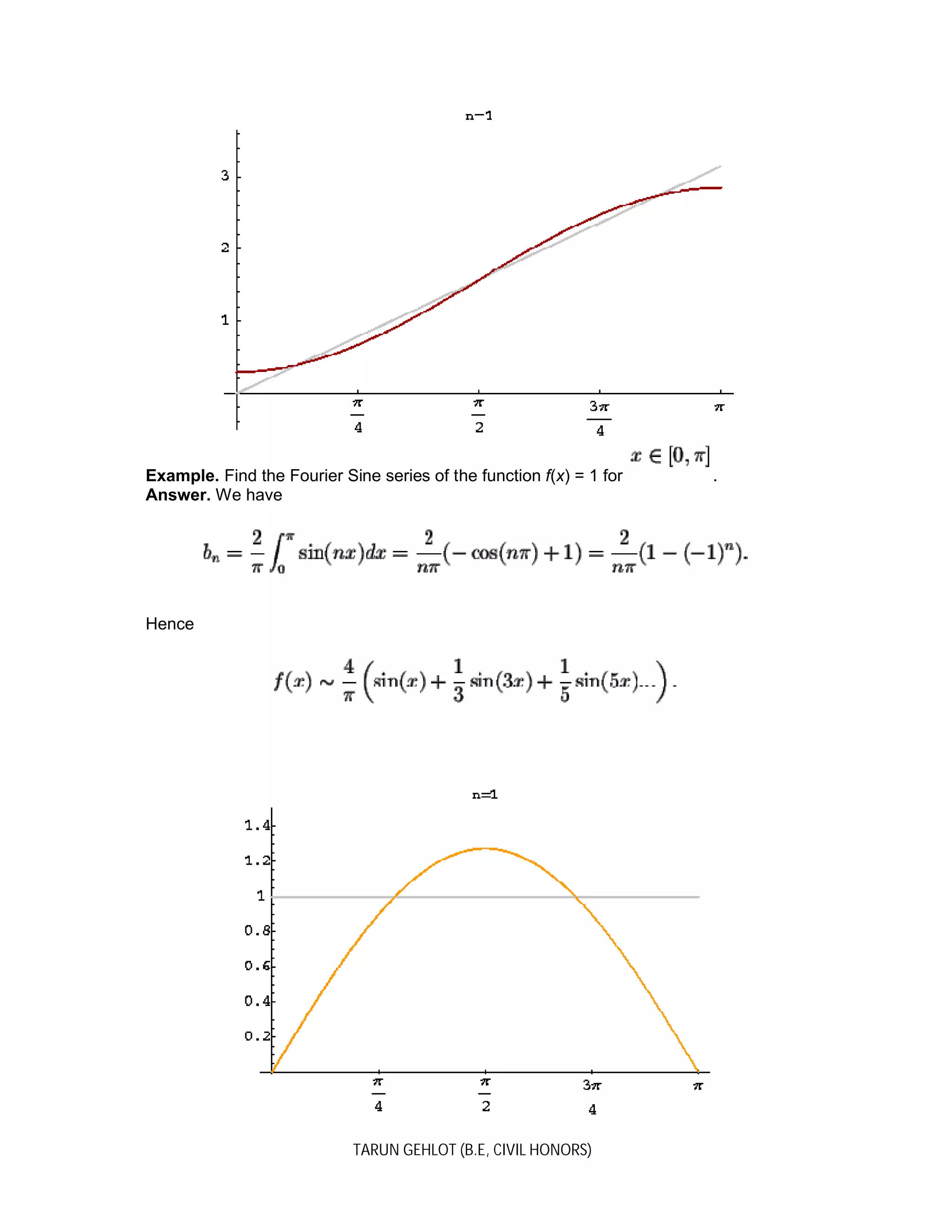
Example. Find the Fourier Sine series of the function
Answer. We have
which gives b1 = 0 and for n > 1, we obtain
Hence
Special Case of 2L-periodic functions.
As we did for -periodic functions, we can define
for functions defined on the interval [
TARUN GEHLOT (B.E, CIVIL HONORS)
Find the Fourier Sine series of the function for
> 1, we obtain
periodic functions.
periodic functions, we can define the Fourier Sine and Cosine series
for functions defined on the interval [-L,L]. First, recall the Fourier series of f(
.
the Fourier Sine and Cosine series
(x)

6. TARUN GEHLOT (B.E, CIVIL HONORS)
where
for .
1.
If f(x) is even, then bn = 0, for . Moreover, we have
and
Finally, we have
2.
If f(x) is odd, then an = 0, for all , and
Finally, we have

7. TARUN GEHLOT (B.E, CIVIL HONORS)