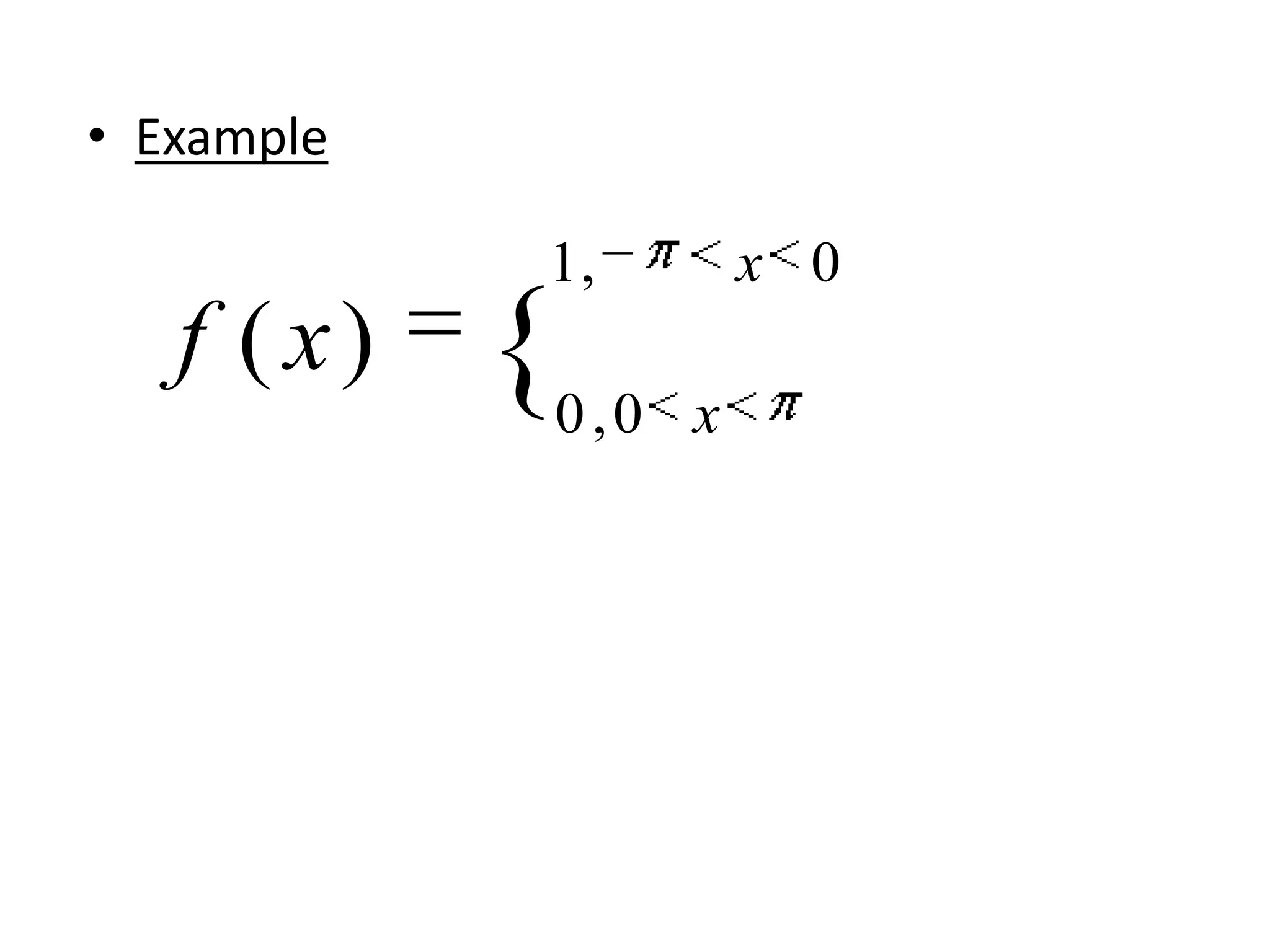Complex form fourier series
•Download as PPTX, PDF•
4 likes•5,425 views
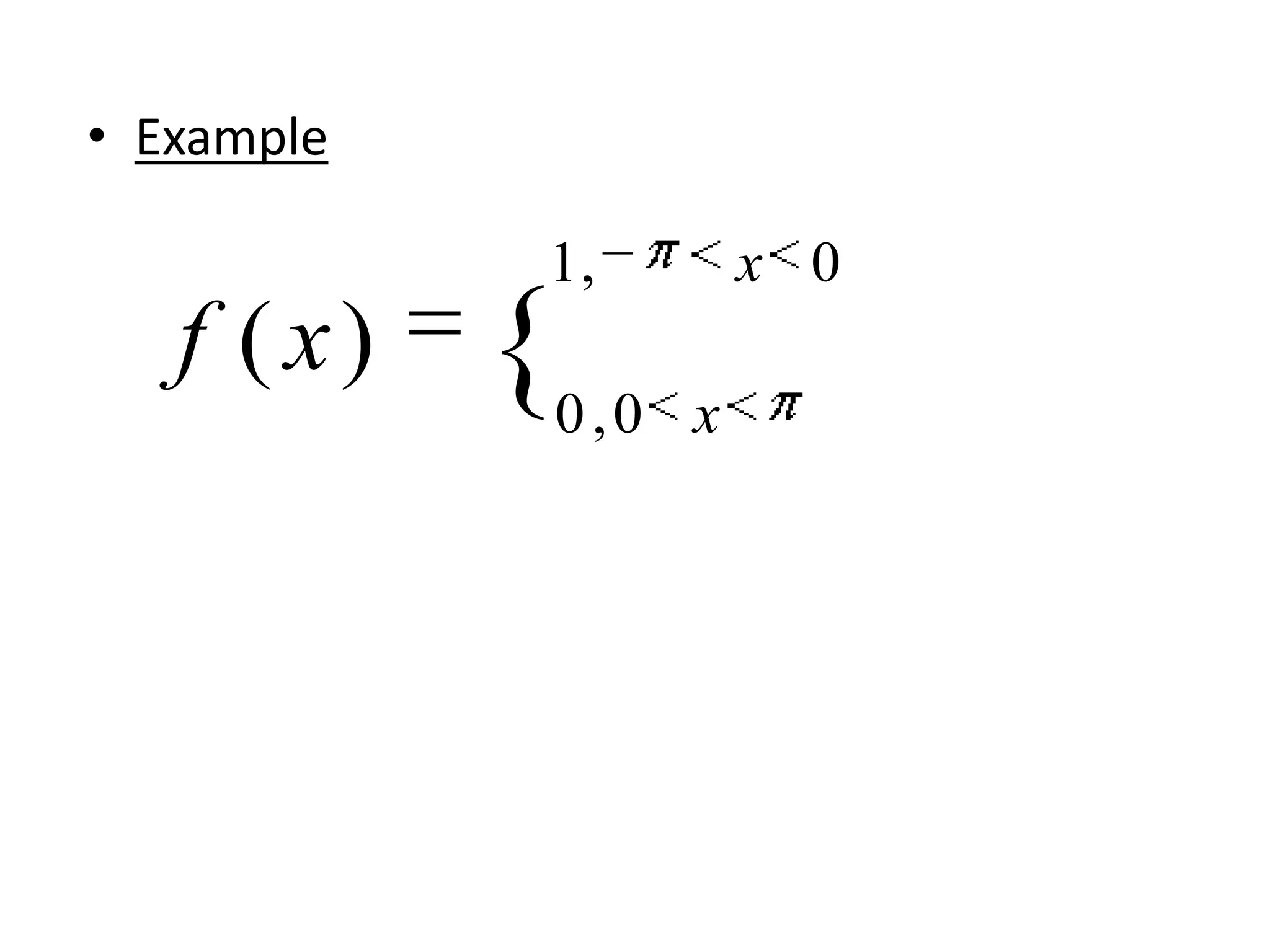
The document summarizes the complex form of Fourier series. It states that after substituting sine and cosine terms into the Fourier series formula, the complex form involves a summation of terms with coefficients multiplied by exponential terms with integer multiples of i and x. It provides the formulas for calculating the coefficients c0, c1, c2, etc. and gives an example function defined over an interval to demonstrate the complex form.
Report
Share
Report
Share
Recommended
Fourier series Introduction
Its states Periodic function, Fourier series for disontinous function, Fourier series, Intervals, Odd and even functions, Half range fourier series etc. Mostly used as active learning assignment in Degree 3rd sem students.
Fourier Transform
The document discusses the Fourier transform, which represents signals in terms of their frequencies rather than polynomials. It originated from Jean Fourier's idea that periodic functions can be represented as a weighted sum of sines and cosines of different frequencies. The Fourier transform generalizes this idea and represents functions as a sum of waves with different amplitudes and phases. It allows representing signals in the frequency domain rather than the spatial domain, making filtering and solving differential equations easier. The Fourier transform and its inverse are defined mathematically. It has many applications in areas like physics, signal processing, and image analysis.
Fourier series
Presentation on Fourier Series
contents are:-
Euler’s Formula
Functions having point of discontinuity
Change of interval
Even and Odd functions
Half Range series
Harmonic analysis
Fourier series
Fourier series can be used to represent periodic and discontinuous functions. The document discusses:
1. The Fourier series expansion of a sawtooth wave, showing how additional terms improve the accuracy of the representation.
2. How Fourier series are well-suited to represent periodic functions over intervals like [0,2π] since the basis functions are also periodic.
3. An example of using Fourier series to analyze a square wave, finding the coefficients for its expansion in terms of sines and cosines.
Fourier transforms
The Fourier transform is a mathematical tool that transforms functions between the time and frequency domains. It breaks down any function or signal into the frequencies that make it up. This allows analysis of signals in the frequency domain, enabling applications like image and signal processing. The Fourier transform represents functions as a combination of sinusoidal functions like sines and cosines. The inverse Fourier transform reconstructs the original function from its frequency representation. Fourier transforms have many uses including solving differential equations, filtering sound and images, and analyzing signals like heartbeats.
Linear differential equation with constant coefficient
The document discusses linear differential equations with constant coefficients. It defines the order, auxiliary equation, complementary function, particular integral and general solution. It provides examples of determining the complementary function and particular integral for different types of linear differential equations. It also discusses Legendre's linear equations, Cauchy-Euler equations, and solving simultaneous linear differential equations.
Laplace transform
The Laplace transform allows solving differential equations using algebra by transforming differential operators into algebraic operations. It transforms a function of time (f(t)) into a function of a complex variable (F(s)), allowing differential equations describing systems to be solved for variables of interest. Key properties include linearity, time and frequency shifting, and relationships between derivatives, integrals, and the Laplace transform that enable solving differential equations by taking the transform, performing algebra, and applying the inverse transform.
Properties of fourier transform
The document discusses 11 properties of the Fourier transform: (1) Linearity and superposition, (2) Time scaling, (3) Time shifting, (4) Duality or symmetry, (5) Area under the time domain function equals the Fourier transform at f=0, (6) Area under the Fourier transform equals the time domain function at t=0, (7) Frequency shifting, (8) Differentiation in the time domain, (9) Integration in the time domain, (10) Multiplication in the time domain becomes convolution in the frequency domain, and (11) Convolution in the time domain becomes multiplication in the frequency domain. Each property is explained briefly.
Recommended
Fourier series Introduction
Its states Periodic function, Fourier series for disontinous function, Fourier series, Intervals, Odd and even functions, Half range fourier series etc. Mostly used as active learning assignment in Degree 3rd sem students.
Fourier Transform
The document discusses the Fourier transform, which represents signals in terms of their frequencies rather than polynomials. It originated from Jean Fourier's idea that periodic functions can be represented as a weighted sum of sines and cosines of different frequencies. The Fourier transform generalizes this idea and represents functions as a sum of waves with different amplitudes and phases. It allows representing signals in the frequency domain rather than the spatial domain, making filtering and solving differential equations easier. The Fourier transform and its inverse are defined mathematically. It has many applications in areas like physics, signal processing, and image analysis.
Fourier series
Presentation on Fourier Series
contents are:-
Euler’s Formula
Functions having point of discontinuity
Change of interval
Even and Odd functions
Half Range series
Harmonic analysis
Fourier series
Fourier series can be used to represent periodic and discontinuous functions. The document discusses:
1. The Fourier series expansion of a sawtooth wave, showing how additional terms improve the accuracy of the representation.
2. How Fourier series are well-suited to represent periodic functions over intervals like [0,2π] since the basis functions are also periodic.
3. An example of using Fourier series to analyze a square wave, finding the coefficients for its expansion in terms of sines and cosines.
Fourier transforms
The Fourier transform is a mathematical tool that transforms functions between the time and frequency domains. It breaks down any function or signal into the frequencies that make it up. This allows analysis of signals in the frequency domain, enabling applications like image and signal processing. The Fourier transform represents functions as a combination of sinusoidal functions like sines and cosines. The inverse Fourier transform reconstructs the original function from its frequency representation. Fourier transforms have many uses including solving differential equations, filtering sound and images, and analyzing signals like heartbeats.
Linear differential equation with constant coefficient
The document discusses linear differential equations with constant coefficients. It defines the order, auxiliary equation, complementary function, particular integral and general solution. It provides examples of determining the complementary function and particular integral for different types of linear differential equations. It also discusses Legendre's linear equations, Cauchy-Euler equations, and solving simultaneous linear differential equations.
Laplace transform
The Laplace transform allows solving differential equations using algebra by transforming differential operators into algebraic operations. It transforms a function of time (f(t)) into a function of a complex variable (F(s)), allowing differential equations describing systems to be solved for variables of interest. Key properties include linearity, time and frequency shifting, and relationships between derivatives, integrals, and the Laplace transform that enable solving differential equations by taking the transform, performing algebra, and applying the inverse transform.
Properties of fourier transform
The document discusses 11 properties of the Fourier transform: (1) Linearity and superposition, (2) Time scaling, (3) Time shifting, (4) Duality or symmetry, (5) Area under the time domain function equals the Fourier transform at f=0, (6) Area under the Fourier transform equals the time domain function at t=0, (7) Frequency shifting, (8) Differentiation in the time domain, (9) Integration in the time domain, (10) Multiplication in the time domain becomes convolution in the frequency domain, and (11) Convolution in the time domain becomes multiplication in the frequency domain. Each property is explained briefly.
Differential equations
1. Differential equations are equations involving derivatives of an unknown function and can be of different orders. Separable differential equations can be expressed as the product of a function of x and a function of y.
2. The general solution or family of solutions to a differential equation represents all possible solutions as determined by initial or boundary conditions. Initial value problems find a particular solution satisfying given initial conditions.
3. Models of natural growth and decay can be represented by differential equations where the rate of change is proportional to the amount present, with solutions in the form of exponential functions. The logistic growth model accounts for limiting factors with a carrying capacity.
Laplace transform
The document discusses the Laplace transform and its applications. Specifically:
- The Laplace transform was developed by mathematicians including Euler, Lagrange, and Laplace to solve differential equations.
- It transforms a function of time to a function of complex frequencies, allowing differential equations to be written as algebraic equations.
- For a function to have a Laplace transform, it must be at least piecewise continuous and bounded above by an exponential function.
- The Laplace transform can reduce the dimension of partial differential equations and is used in applications including semiconductor mobility, wireless networks, vehicle vibrations, and electromagnetic fields.
Fourier series
The document discusses Fourier series and two of their applications. Fourier series can be used to represent periodic functions as an infinite series of sines and cosines. This allows approximating functions that are not smooth using trigonometric polynomials. Two key applications are representing forced oscillations, where a periodic driving force can be modeled as a Fourier series, and solving the heat equation, where the method of separation of variables results in a Fourier series representation of temperature over space and time.
Fourier transform
Fourier Transform ,Time Domain representation of the signal
Frequency Domain representation of the signal
Z Transform
The document discusses the Z-transform, which is the discrete-time equivalent of the Laplace transform. Some key points covered include:
- The Z-transform is used to analyze discrete-time signals and discrete-time systems. It allows representation in the frequency domain through pole-zero analysis.
- Causal, anti-causal, and two-sided sequences have different regions of convergence for their Z-transforms. Stability depends on poles lying inside or outside the unit circle.
- The Z-transform has various properties that allow computations and transformations. The inverse Z-transform can be obtained through techniques like partial fraction expansion or long division.
Second order homogeneous linear differential equations
1) The document discusses second order linear homogeneous differential equations, which have the general form P(x)y'' + Q(x)y' + R(x)y = 0.
2) It describes methods for finding the general solution including reduction of order, and discusses the solutions when the coefficients are constants.
3) The general solution depends on the nature of the roots of the auxiliary equation: distinct real roots, repeated real roots, or complex roots.
Cauchy integral theorem & formula (complex variable & numerical method )
1) The document discusses the Cauchy Integral Theorem and Formula. It states that if a function f(z) is analytic inside and on a closed curve C, then the integral of f(z) around C is equal to 0.
2) It provides examples of evaluating integrals using the Cauchy Integral Theorem when the singularities lie outside the closed curve C.
3) The Cauchy Integral Formula is introduced, which expresses the value of an analytic function F(a) inside C as a contour integral around C. Examples are worked out applying this formula to find the value and derivatives of functions at points inside C.
Laplace transform & fourier series
1. The document defines the Fourier series as an expansion of a function in a series of sines and cosines.
2. Fourier series can be used to represent even functions as a cosine series and odd functions as a sine series.
3. Examples are provided of calculating the Fourier coefficients for different functions, including finding the Fourier series of the function f(x)=x on the interval [0,π].
Fourier Series - Engineering Mathematics
In this slide fourier series of Engineering Mathematics has been described. one Example is also added for you. Hope this will help you understand fourier series.
Laplace Transformation & Its Application
This document presents an overview of the Laplace transform and its applications. It begins with an introduction to Laplace transforms as a mathematical tool to convert differential equations into algebraic expressions. It then provides definitions and properties of both the Laplace transform and its inverse. Examples are given of how Laplace transforms can be used to solve ordinary and partial differential equations, as well as applications in electrical circuits and other fields. The document concludes by noting some limitations of the Laplace transform method and references additional resources.
Presentation on laplace transforms
- The Laplace transform is a linear operator that transforms a function of time (f(t)) into a function of complex frequency (F(s)). It was developed from the work of mathematicians like Euler, Lagrange, and Laplace.
- The Laplace transform has many applications in fields like semiconductor mobility, wireless network call completion, vehicle vibration analysis, and modeling electric and magnetic fields. It allows transforming differential equations into algebraic equations that are easier to solve.
- For example, in semiconductors with varying material layers, the Laplace transform can relate the conductivity tensor to the Laplace transforms of electron and hole densities, enabling the determination of key properties like carrier concentration and mobility in each layer.
Unit step function
The document discusses unit step functions and their use in describing abrupt changes in function values that occur at specific times, such as a voltage being switched on or off in an electrical circuit. It defines the unit step function u(t) as having a value of 0 for negative t and 1 for positive t. Shifted and rectangular pulse functions are also described. Examples are provided of writing functions in terms of unit step functions and sketching the corresponding waveforms.
Methods of solving ODE
This presentation gives the basic idea about the methods of solving ODEs
The methods like variation of parameters, undetermined coefficient method, 1/f(D) method, Particular integral and complimentary functions of an ODE
Fourier series and transforms
This document discusses Fourier series and transforms. It begins by introducing periodic functions and their fundamental periods. It then defines Fourier series and derives the formulas for the Fourier coefficients. Several examples of calculating Fourier series are provided. It also covers Fourier series for functions with any period, complex Fourier series, Parseval's identity and its applications, and Dirichlet's theorem. The key topics of Fourier series, Fourier transforms, and their applications in engineering mathematics are covered over multiple sections.
Using Laplace Transforms to Solve Differential Equations
This document discusses using Laplace transforms to solve differential equations. It begins with an introduction to Laplace transforms and their inventor Pierre-Simon Laplace. The author then explains that Laplace transforms can be used to transform differential equations into simpler algebraic equations that are easier to solve. As an example, the document walks through using Laplace transforms to solve a first order differential equation. It concludes that Laplace transforms are an important mathematical tool for solving differential equations.
Fourier series and fourier integral
- The document discusses Fourier series and integrals.
- Fourier series decomposes a periodic function into a sum of sines and cosines. It is useful for representing periodic and discontinuous functions.
- There are three types of Fourier integrals: the general Fourier integral, Fourier cosine integral, and Fourier sine integral. These are used to represent functions over infinite intervals.
fourier transforms
The document provides an overview of Fourier transforms. It begins by introducing Fourier series which deals with continuous-time periodic signals and results in discrete frequency spectra. It then discusses how the Fourier integral and continuous Fourier transform can deal with aperiodic signals by providing continuous spectra. The continuous Fourier transform represents a function as an integral of its frequencies, while the inverse transform uses this representation to recover the original function. The properties of the Fourier transform discussed include linearity, time scaling, time reversal, time shifting, and frequency shifting. Real functions have special properties where the Fourier transform is always real or pure imaginary. Examples are provided to illustrate how to calculate the Fourier transform of simple functions.
Fourier transform
This presentation describes the Fourier Transform used in different mathematical and physical applications.
The presentation is at an Undergraduate in Science (math, physics, engineering) level.
Please send comments and suggestions to improvements to solo.hermelin@gmail.com.
More presentations can be found at my website http://www.solohermelin.com.
Laplace transform
The document presents information about Laplace transforms including:
- The definition and properties of the Laplace transform. It transforms differential equations into algebraic equations.
- Examples of applications in solving ordinary and partial differential equations, electrical circuits, and other fields.
- Limitations in that it can only be used to solve differential equations with known constants.
- Conclusion that the Laplace transform is a powerful mathematical tool used across many areas of science and engineering.
Optics Fourier Transform Ii
The document discusses several key concepts related to the Fourier transform:
1) It introduces the Dirac delta function and explains how it relates to the Fourier transform of exponential and cosine functions.
2) It describes several theorems regarding how the Fourier transform is affected by scaling, shifting, summing and differentiating functions.
3) It explains that both the intensity and phase of a time domain function, and the spectral intensity and phase in the frequency domain, are needed to fully characterize the function and its Fourier transform.
Fisika Matematika I (9 - 10) Deret fourier
The document discusses the Fourier series and its use in solving problems. It introduces the Fourier series and its trigonometric form. It then presents a example problem involving using a Fourier series to determine the power lost when passing a sawtooth wave through a communication channel that filters out frequencies above 5.5 Hz. The solution finds the Fourier series representation of the sawtooth wave, then calculates the power in the first 5 harmonics to obtain the power transmitted by the channel and the 0.51 dB power loss.
Admission in India
The document discusses Fourier series and their application to periodic functions. It introduces periodic functions and their properties. Fourier series can be used to decompose any periodic function into a sum of sines and cosines. This allows periodic waveforms to be analyzed and approximated as the sum of their harmonic components. Examples are provided to demonstrate how to calculate the Fourier series of simple periodic functions like square waves.
More Related Content
What's hot
Differential equations
1. Differential equations are equations involving derivatives of an unknown function and can be of different orders. Separable differential equations can be expressed as the product of a function of x and a function of y.
2. The general solution or family of solutions to a differential equation represents all possible solutions as determined by initial or boundary conditions. Initial value problems find a particular solution satisfying given initial conditions.
3. Models of natural growth and decay can be represented by differential equations where the rate of change is proportional to the amount present, with solutions in the form of exponential functions. The logistic growth model accounts for limiting factors with a carrying capacity.
Laplace transform
The document discusses the Laplace transform and its applications. Specifically:
- The Laplace transform was developed by mathematicians including Euler, Lagrange, and Laplace to solve differential equations.
- It transforms a function of time to a function of complex frequencies, allowing differential equations to be written as algebraic equations.
- For a function to have a Laplace transform, it must be at least piecewise continuous and bounded above by an exponential function.
- The Laplace transform can reduce the dimension of partial differential equations and is used in applications including semiconductor mobility, wireless networks, vehicle vibrations, and electromagnetic fields.
Fourier series
The document discusses Fourier series and two of their applications. Fourier series can be used to represent periodic functions as an infinite series of sines and cosines. This allows approximating functions that are not smooth using trigonometric polynomials. Two key applications are representing forced oscillations, where a periodic driving force can be modeled as a Fourier series, and solving the heat equation, where the method of separation of variables results in a Fourier series representation of temperature over space and time.
Fourier transform
Fourier Transform ,Time Domain representation of the signal
Frequency Domain representation of the signal
Z Transform
The document discusses the Z-transform, which is the discrete-time equivalent of the Laplace transform. Some key points covered include:
- The Z-transform is used to analyze discrete-time signals and discrete-time systems. It allows representation in the frequency domain through pole-zero analysis.
- Causal, anti-causal, and two-sided sequences have different regions of convergence for their Z-transforms. Stability depends on poles lying inside or outside the unit circle.
- The Z-transform has various properties that allow computations and transformations. The inverse Z-transform can be obtained through techniques like partial fraction expansion or long division.
Second order homogeneous linear differential equations
1) The document discusses second order linear homogeneous differential equations, which have the general form P(x)y'' + Q(x)y' + R(x)y = 0.
2) It describes methods for finding the general solution including reduction of order, and discusses the solutions when the coefficients are constants.
3) The general solution depends on the nature of the roots of the auxiliary equation: distinct real roots, repeated real roots, or complex roots.
Cauchy integral theorem & formula (complex variable & numerical method )
1) The document discusses the Cauchy Integral Theorem and Formula. It states that if a function f(z) is analytic inside and on a closed curve C, then the integral of f(z) around C is equal to 0.
2) It provides examples of evaluating integrals using the Cauchy Integral Theorem when the singularities lie outside the closed curve C.
3) The Cauchy Integral Formula is introduced, which expresses the value of an analytic function F(a) inside C as a contour integral around C. Examples are worked out applying this formula to find the value and derivatives of functions at points inside C.
Laplace transform & fourier series
1. The document defines the Fourier series as an expansion of a function in a series of sines and cosines.
2. Fourier series can be used to represent even functions as a cosine series and odd functions as a sine series.
3. Examples are provided of calculating the Fourier coefficients for different functions, including finding the Fourier series of the function f(x)=x on the interval [0,π].
Fourier Series - Engineering Mathematics
In this slide fourier series of Engineering Mathematics has been described. one Example is also added for you. Hope this will help you understand fourier series.
Laplace Transformation & Its Application
This document presents an overview of the Laplace transform and its applications. It begins with an introduction to Laplace transforms as a mathematical tool to convert differential equations into algebraic expressions. It then provides definitions and properties of both the Laplace transform and its inverse. Examples are given of how Laplace transforms can be used to solve ordinary and partial differential equations, as well as applications in electrical circuits and other fields. The document concludes by noting some limitations of the Laplace transform method and references additional resources.
Presentation on laplace transforms
- The Laplace transform is a linear operator that transforms a function of time (f(t)) into a function of complex frequency (F(s)). It was developed from the work of mathematicians like Euler, Lagrange, and Laplace.
- The Laplace transform has many applications in fields like semiconductor mobility, wireless network call completion, vehicle vibration analysis, and modeling electric and magnetic fields. It allows transforming differential equations into algebraic equations that are easier to solve.
- For example, in semiconductors with varying material layers, the Laplace transform can relate the conductivity tensor to the Laplace transforms of electron and hole densities, enabling the determination of key properties like carrier concentration and mobility in each layer.
Unit step function
The document discusses unit step functions and their use in describing abrupt changes in function values that occur at specific times, such as a voltage being switched on or off in an electrical circuit. It defines the unit step function u(t) as having a value of 0 for negative t and 1 for positive t. Shifted and rectangular pulse functions are also described. Examples are provided of writing functions in terms of unit step functions and sketching the corresponding waveforms.
Methods of solving ODE
This presentation gives the basic idea about the methods of solving ODEs
The methods like variation of parameters, undetermined coefficient method, 1/f(D) method, Particular integral and complimentary functions of an ODE
Fourier series and transforms
This document discusses Fourier series and transforms. It begins by introducing periodic functions and their fundamental periods. It then defines Fourier series and derives the formulas for the Fourier coefficients. Several examples of calculating Fourier series are provided. It also covers Fourier series for functions with any period, complex Fourier series, Parseval's identity and its applications, and Dirichlet's theorem. The key topics of Fourier series, Fourier transforms, and their applications in engineering mathematics are covered over multiple sections.
Using Laplace Transforms to Solve Differential Equations
This document discusses using Laplace transforms to solve differential equations. It begins with an introduction to Laplace transforms and their inventor Pierre-Simon Laplace. The author then explains that Laplace transforms can be used to transform differential equations into simpler algebraic equations that are easier to solve. As an example, the document walks through using Laplace transforms to solve a first order differential equation. It concludes that Laplace transforms are an important mathematical tool for solving differential equations.
Fourier series and fourier integral
- The document discusses Fourier series and integrals.
- Fourier series decomposes a periodic function into a sum of sines and cosines. It is useful for representing periodic and discontinuous functions.
- There are three types of Fourier integrals: the general Fourier integral, Fourier cosine integral, and Fourier sine integral. These are used to represent functions over infinite intervals.
fourier transforms
The document provides an overview of Fourier transforms. It begins by introducing Fourier series which deals with continuous-time periodic signals and results in discrete frequency spectra. It then discusses how the Fourier integral and continuous Fourier transform can deal with aperiodic signals by providing continuous spectra. The continuous Fourier transform represents a function as an integral of its frequencies, while the inverse transform uses this representation to recover the original function. The properties of the Fourier transform discussed include linearity, time scaling, time reversal, time shifting, and frequency shifting. Real functions have special properties where the Fourier transform is always real or pure imaginary. Examples are provided to illustrate how to calculate the Fourier transform of simple functions.
Fourier transform
This presentation describes the Fourier Transform used in different mathematical and physical applications.
The presentation is at an Undergraduate in Science (math, physics, engineering) level.
Please send comments and suggestions to improvements to solo.hermelin@gmail.com.
More presentations can be found at my website http://www.solohermelin.com.
Laplace transform
The document presents information about Laplace transforms including:
- The definition and properties of the Laplace transform. It transforms differential equations into algebraic equations.
- Examples of applications in solving ordinary and partial differential equations, electrical circuits, and other fields.
- Limitations in that it can only be used to solve differential equations with known constants.
- Conclusion that the Laplace transform is a powerful mathematical tool used across many areas of science and engineering.
Optics Fourier Transform Ii
The document discusses several key concepts related to the Fourier transform:
1) It introduces the Dirac delta function and explains how it relates to the Fourier transform of exponential and cosine functions.
2) It describes several theorems regarding how the Fourier transform is affected by scaling, shifting, summing and differentiating functions.
3) It explains that both the intensity and phase of a time domain function, and the spectral intensity and phase in the frequency domain, are needed to fully characterize the function and its Fourier transform.
What's hot (20)
Second order homogeneous linear differential equations
Second order homogeneous linear differential equations
Cauchy integral theorem & formula (complex variable & numerical method )
Cauchy integral theorem & formula (complex variable & numerical method )
Using Laplace Transforms to Solve Differential Equations
Using Laplace Transforms to Solve Differential Equations
Viewers also liked
Fisika Matematika I (9 - 10) Deret fourier
The document discusses the Fourier series and its use in solving problems. It introduces the Fourier series and its trigonometric form. It then presents a example problem involving using a Fourier series to determine the power lost when passing a sawtooth wave through a communication channel that filters out frequencies above 5.5 Hz. The solution finds the Fourier series representation of the sawtooth wave, then calculates the power in the first 5 harmonics to obtain the power transmitted by the channel and the 0.51 dB power loss.
Admission in India
The document discusses Fourier series and their application to periodic functions. It introduces periodic functions and their properties. Fourier series can be used to decompose any periodic function into a sum of sines and cosines. This allows periodic waveforms to be analyzed and approximated as the sum of their harmonic components. Examples are provided to demonstrate how to calculate the Fourier series of simple periodic functions like square waves.
Group 4 physics
The document describes someone who is really good at math, making and interpreting graphs, linking concepts to solve problems, writing detailed lab reports, and working organized and disciplined every day. They are willing to ask for help when needed and are considering studying engineering as they like physics but are not great at math.
Mathematical physics group 16
The average value of a function f(x) over an interval (a,b) can be approximated as:
f(x) = (f(x1) + f(x2) + ... + f(xn))/n, where x1, x2, ..., xn are values in the interval.
The Fourier coefficients for a periodic function f(x) are:
a0 = (1/π) ∫ f(x) dx
an = (2/π) ∫ f(x) cos(nx) dx
bn = (2/π) ∫ f(x) sin(nx) dx
The Fourier series expansion of
Fourier sine and cosine series
The document discusses Fourier series and their application to functions defined over intervals. It defines the Fourier sine and cosine series for functions on [-L,L] by extending the functions to the full interval [-π,π] in an odd or even way. The Fourier sine series results from the odd extension, using sine terms, while the Fourier cosine series uses the even extension and cosine terms. Examples are provided of calculating the Fourier sine and cosine series for basic functions over [-1,1]. The approach generalizes to 2L-periodic functions defined on [-L,L].
High Precision, Not High Energy: Using Atomic Physics to Look Beyond the Stan...
First of two lectures on atomic physics searches for exotic physics, given at the Nordita Workshop for Science Writers on Quantum Theory.
Chapter 15 and 16 questions and answers GCE OCR ADVANCING PHYSICS B
This document does not contain any meaningful content to summarize. It consists of two chapter numbers followed by a series of blank lines. A proper summary cannot be generated without substantive information in the original document.
Half range sine cosine fourier series
The document discusses half range Fourier series representations of functions defined on an interval (0, L). It explains that a periodic extension F(x) of period 2L can be constructed from the function f(x) defined on (0, L). This extended function F(x) is then expanded into either a Fourier sine series or cosine series. The coefficients of these series represent the half range Fourier sine or cosine series for the original function f(x) defined on the interval (0, L).
Half range sine and cosine series
The document discusses half-range Fourier series expansions for functions defined over a finite interval. Specifically, it explains that if a function f(x) is even or odd over the interval [0,L], it can be expressed using either a cosine or sine series just over the interval [0,L]. This is referred to as a half-range Fourier series. Examples are provided of using half-range sine and cosine series to expand specific functions like f(x)=x2 and f(x)=x over intervals like [0,l].
Accelerators and Applications- Summer Training in Physics 16
Particle accelerators are used to study nuclear structure by providing high energies needed to see subatomic details. They work by using electric fields to accelerate charged particles, gaining kinetic energy. Accelerators are essential for understanding materials through techniques like Rutherford backscattering spectroscopy (RBS) which uses ion beams and detection of backscattered ions to determine thickness, composition, and depth profiling of materials. Key applications of accelerators include ion implantation to dope materials, cancer treatment, materials characterization using techniques like RBS, and transmuting nuclear waste.
History and Real Life Applications of Fourier Analaysis
This document discusses the history and applications of Fourier analysis. It notes that Fourier analysis was invented by Jean Baptiste Joseph Fourier, a French mathematician and physicist born in the late 18th century. The document then lists some of the main applications of Fourier analysis, such as signal processing, image processing, heat distribution mapping, wave simplification, and light simplification. It provides examples of how Fourier analysis can be used to transform signals from the time domain to the frequency domain using Fourier series equations. Charts are shown demonstrating this transformation for simple sine waves. The document cautions that Fourier analysis works best for stationary waves and that more advanced techniques are needed for non-stationary waves like music or speech.
Group theory
contains adequate info. about group theory...some contents are not seen coz...thr r images on top of the info.... wud suggest to download and see the ppt on slideshow...content is good and adequate..!!
Group theory questions and answers
This document discusses group theory and symmetry elements as they relate to several different molecules. It provides examples of identifying the point groups, symmetry elements like rotation axes and planes of inversion, and determining the representations of atomic and molecular orbitals for molecules like ammonia, acetone, ethanediol, propadiene, water, BH3, cyclopropenyl cation, butadiene, and trichlorborane. Worked examples are provided to demonstrate how to analyze symmetry properties and construct molecular orbital diagrams for various systems.
GROUP THEORY ( SYMMETRY)
The document discusses symmetry operations and point groups in molecules. It defines five basic symmetry operations: identity, n-fold rotation, reflection, inversion, and improper n-fold rotation. Point groups describe the symmetry elements and operations in a molecule. There are 32 possible point groups that molecules can belong to depending on their specific symmetry properties. The document provides examples of molecules and their corresponding point groups.
fourier series
The document discusses Fourier series, which represent periodic functions as an infinite series of sines and cosines. Fourier series can be used to represent functions that are discontinuous or non-differentiable. The key formulas for the Fourier series coefficients are presented. Fourier series expansions take different forms depending on whether the function is even, odd, or defined on different intervals. Half-range Fourier series are also discussed as representations of functions defined on half periods.
Solid state physics d r joshi
This document provides an introduction to solid state physics presented by Dr. Dattu Joshi. It discusses the aims of solid state physics, including understanding the properties of solids based on the interactions between atomic nuclei and electrons. It describes crystalline solids as having a regular repeated atomic pattern and discusses different types of solids including crystalline, polycrystalline, and amorphous materials. The document outlines several topics that will be covered related to crystal structure, diffraction, imperfections, and bonding in solids.
The Fast Fourier Transform (FFT)
The discrete Fourier transform has many applications in science and engineering. For example, it is often used in digital signal processing applications such as voice recognition and image processing.
Physics form 4 chapter1 slides
1) Physics is the study of natural phenomena involving force, matter, and energy. It uses experimental observation and quantitative measurement.
2) There are base quantities like mass, time, and length that cannot be defined by other quantities, and derived quantities like volume and velocity that are calculated from base quantities.
3) Measurements in physics aim for both accuracy, being close to the true value, and consistency, having results that are close together. Instruments have varying levels of sensitivity to allow for small measurements.
Quantum Mechanics Presentation
Quantum mechanics is a new way of understanding the atomic world based on quanta or packets of energy. Light can behave as both a particle and a wave, with photons as quanta of light energy. The photoelectric effect and emission line spectra provided evidence that light behaves as quanta that can be absorbed or emitted in specific amounts of energy. Bohr's model of the hydrogen atom explained transitions between discrete energy levels by quantization of angular momentum and energy.
Introduction to group theory
This document discusses group theory and symmetry elements in chemistry. It defines symmetry elements as geometrical entities like points, lines, or planes that objects can be rotated or reflected around. Common symmetry operations are rotation, reflection, and inversion. Examples of symmetry elements include axes of rotation, planes of reflection, and centers of inversion. Several molecules like water, carbon dioxide, ethene, benzene, and ruthenium complexes are analyzed to identify their specific symmetry elements and point groups.
Viewers also liked (20)
High Precision, Not High Energy: Using Atomic Physics to Look Beyond the Stan...
High Precision, Not High Energy: Using Atomic Physics to Look Beyond the Stan...
Chapter 15 and 16 questions and answers GCE OCR ADVANCING PHYSICS B
Chapter 15 and 16 questions and answers GCE OCR ADVANCING PHYSICS B
Accelerators and Applications- Summer Training in Physics 16
Accelerators and Applications- Summer Training in Physics 16
History and Real Life Applications of Fourier Analaysis
History and Real Life Applications of Fourier Analaysis
Similar to Complex form fourier series
Engr 213 final 2009
This document contains a 9 question final exam for an applied ordinary differential equations engineering course. The questions cover a range of topics including: finding general and particular solutions to 1st and 2nd order differential equations using various methods; solving initial value problems; solving systems of differential equations; power series solutions; and modeling an LRC circuit with a differential equation. Students are given 3 hours to complete the exam worth a total of 100 points.
Welcome to International Journal of Engineering Research and Development (IJERD)
The document discusses L1-convergence of the Rees-Stanojević modified cosine sum. It contains the following key points:
1. The author obtains a necessary and sufficient condition for L1-convergence of the Rees-Stanojević sum under the condition that the Fourier coefficients satisfy a certain limit.
2. This generalizes a previous result by Garrett and Stanojević which proved convergence in the L-metric for quasi-convex sequences.
3. As a corollary, the author shows that the L1-convergence of the partial sums of the cosine series is equivalent to the condition that the product of the largest neglected coefficient and log n approaches 0 as n approaches
Assignment6
This document contains instructions for 5 assignment questions involving numerical integration and solving differential equations. Question 1 involves using the quad function to evaluate several integrals. Question 2 involves using quad to evaluate Fresnel integrals and plot the results. Question 3 involves using Monte Carlo methods to estimate volumes and double integrals. Question 4 involves using Euler's method to solve an initial value problem and analyze errors. Question 5 involves using lsode to solve a system of differential equations modeling atmospheric circulation and experimenting with initial conditions.
IJCER (www.ijceronline.com) International Journal of computational Engineerin...
This document summarizes a study on the Lp-convergence of the Rees-Stanojevic modified cosine sum for 0 < p < 1. It presents a theorem showing that if the sequence {ak} satisfies conditions ak → 0 and Σ|Δak| < ∞, then the limit of the integral of |f(x) - hn(x)|p dx from -π to π is 0 as n → ∞. It also includes a corollary deducing an earlier theorem by Ul'yanov as a special case where hn(x) is replaced with the partial sum Sn(x).
Lesson 28: The Fundamental Theorem of Calculus
This document contains lecture notes on the Fundamental Theorem of Calculus. It begins with announcements about the final exam date and current grade distribution. The outline then reviews the Evaluation Theorem and introduces the First and Second Fundamental Theorems of Calculus. It provides examples of how the integral can represent total change in concepts like distance, cost, and mass. Biographies are also included of mathematicians like Gregory, Barrow, Newton, and Leibniz who contributed to the development of calculus.
Lesson 28: The Fundamental Theorem of Calculus
This document contains notes from a calculus class. It provides the outline and key points about the Fundamental Theorem of Calculus. It discusses the first and second Fundamental Theorems of Calculus, including proofs and examples. It also provides brief biographies of several important mathematicians that contributed to the development of calculus, including the Fundamental Theorem of Calculus, such as Isaac Newton, Gottfried Leibniz, James Gregory, and Isaac Barrow.
Formula List Math 1230
The document lists 4 formulas relevant to a Math 1230 course:
1) Euler's method for numerical integration of differential equations.
2) Formulas for finding the centroid (center of mass) of a plane region and the average value of a function over that region.
3) Taylor series representation of functions, expressing a function as a sum of terms involving its derivatives.
4) Rules for differentiating and integrating power series representations of functions.
Md2521102111
IJERA (International journal of Engineering Research and Applications) is International online, ... peer reviewed journal. For more detail or submit your article, please visit www.ijera.com
Chapter 2 (maths 3)
The document summarizes Fourier series and related concepts:
1. It defines periodic functions and their periods, gives examples like sin x and cos x having period 2π.
2. It states Dirichlet's conditions for a function to have a Fourier series representation and defines the Fourier coefficients using Euler's formulas.
3. It explains that the Fourier series of an even function contains only cosine terms and of an odd function contains only sine terms.
4. It provides examples of even and odd functions and solves problems finding Fourier series representations of specific functions.
Deflection 2
This document contrasts vector mechanics and variational formulations for structural analysis. It uses the example of a simply supported beam under a uniformly distributed load to illustrate the approaches.
[1] Using vector mechanics, the beam is modeled as discrete elements and equilibrium equations are written for each element and solved. [2] Alternatively, the variational approach introduces a potential energy function for the system and finds the shape that minimizes this function. [3] For the beam example, an approximate solution is first found using a simple shape function, then a more accurate solution is obtained using a shape function with more degrees of freedom that matches the exact solution.
A Novel Methodology for Designing Linear Phase IIR Filters
This paper presents a novel technique for
designing an Infinite Impulse Response (IIR) Filter with
Linear Phase Response. The design of IIR filter is always a
challenging task due to the reason that a Linear Phase
Response is not realizable in this kind. The conventional
techniques involve large number of samples and higher
order filter for better approximation resulting in complex
hardware for implementing the same. In addition, an
extensive computational resource for obtaining the inverse
of huge matrices is required. However, we propose a
technique, which uses the frequency domain sampling along
with the linear programming concept to achieve a filter
design, which gives a best approximation for the linear
phase response. The proposed method can give the closest
response with less number of samples (only 10) and is
computationally simple. We have presented the filter design
along with its formulation and solving methodology.
Numerical results are used to substantiate the efficiency of
the proposed method.
Fourier transform
The Fourier transform decomposes a signal into its constituent frequencies, representing it in the frequency domain rather than the spatial domain, which can make certain operations and analyses easier to perform; it has both magnitude and phase components that provide information about the frequency content and relative phases of the signal. The discrete Fourier transform (DFT) is a sampled version of the continuous Fourier transform that is useful for digital signal and image processing applications.
Lesson 31: Evaluating Definite Integrals
The Second Fundamental Theorem of Calculus allows us to compute definite integrals by antidifferentiation
Fourier series 2
The document discusses the Fourier series representation of periodic functions with an arbitrary period. It provides the general form of the Fourier series for a function f(x) with period 2L, defined over the interval c < x < c + 2L. It also gives the specific forms when c = 0, -L, or L. An example of finding the Fourier series of the function f(x) = x^2 from 0 to 2 is worked out step-by-step.
Welcome to International Journal of Engineering Research and Development (IJERD)
The document presents a theorem that generalizes previous results on the L1-convergence of modified trigonometric cosine sums. Specifically, it obtains a necessary and sufficient condition for the L1-convergence of a modified cosine sum where the coefficients belong to the Fp class. This condition is that an log n = o(1) as n approaches infinity. The theorem also deduces Fomin's previous result as a corollary.
Primer for ordinary differential equations
This document provides an introduction and overview of ordinary differential equations (ODEs). It defines an ODE, distinguishes ODEs from partial differential equations, and outlines techniques for solving linear ODEs with constant coefficients using classical and Laplace transform methods. The document also discusses how engineers formulate and approach solving ODEs based on physical systems and provides examples of solving first and second order linear ODEs.
Reflect tsukuba524
This document summarizes a talk on Lorentz surfaces in pseudo-Riemannian space forms with horizontal reflector lifts. It introduces examples of Lorentz surfaces with zero mean curvature in these spaces. It also discusses reflector spaces and horizontal reflector lifts, and presents a rigidity theorem stating that if two isometric immersions from a Lorentz surface to a pseudo-Riemannian space form both have horizontal reflector lifts and satisfy certain curvature conditions, then the immersions must differ by an isometry of the target space.
Convolution and FFT
1. Polynomials
- Representation
- Convolution
2. Complex Roots of Unity
3. DFT
4. FFT
5. Euler’s formula
Business math
This document provides an introduction to basic definite integration. It defines definite integration as calculating the area under a curve between two limits using antiderivatives. It demonstrates how to calculate definite integrals of simple functions and interpret the results as areas. It also discusses how the sign of the integral depends on whether the function lies above or below the x-axis. Quizzes are included to assess understanding of these concepts.
Introduction to inverse problems
This document provides an introduction to inverse problems and their applications. It summarizes integral equations like Volterra and Fredholm equations of the first and second kind. It also describes inverse problems for partial differential equations, including inverse convection-diffusion, Poisson, and Laplace problems. Applications mentioned include medical imaging, non-destructive testing, and geophysics. Bibliographic references are provided.
Similar to Complex form fourier series (20)
Welcome to International Journal of Engineering Research and Development (IJERD)
Welcome to International Journal of Engineering Research and Development (IJERD)
IJCER (www.ijceronline.com) International Journal of computational Engineerin...
IJCER (www.ijceronline.com) International Journal of computational Engineerin...
A Novel Methodology for Designing Linear Phase IIR Filters
A Novel Methodology for Designing Linear Phase IIR Filters
Welcome to International Journal of Engineering Research and Development (IJERD)
Welcome to International Journal of Engineering Research and Development (IJERD)
Complex form fourier series
- 2. Group 15 1. M. Derry R.A (A1C410210) 2. Hairul Akbar (A1C410211)
- 3. Complex Form Of Fourier Series
- 4. • After we substite sin nx and cos nx to fourier series formula we can get the complex form of fourier series is : inx inx 2 inx 2 inx f ( x) c0 c1 e c 1e c2e c 2e .... 1 With coefficient: c0 f ( x ) dx 2 1 inx cn f ( x )e dx 2
- 5. • Example 1, x 0 f ( x) { 0,0 x
- 6. Other Interval • Fuction of other interval is:
- 8. • Example 0,0 x l f ( x) { 1, l x 2 l
- 9. Thank you