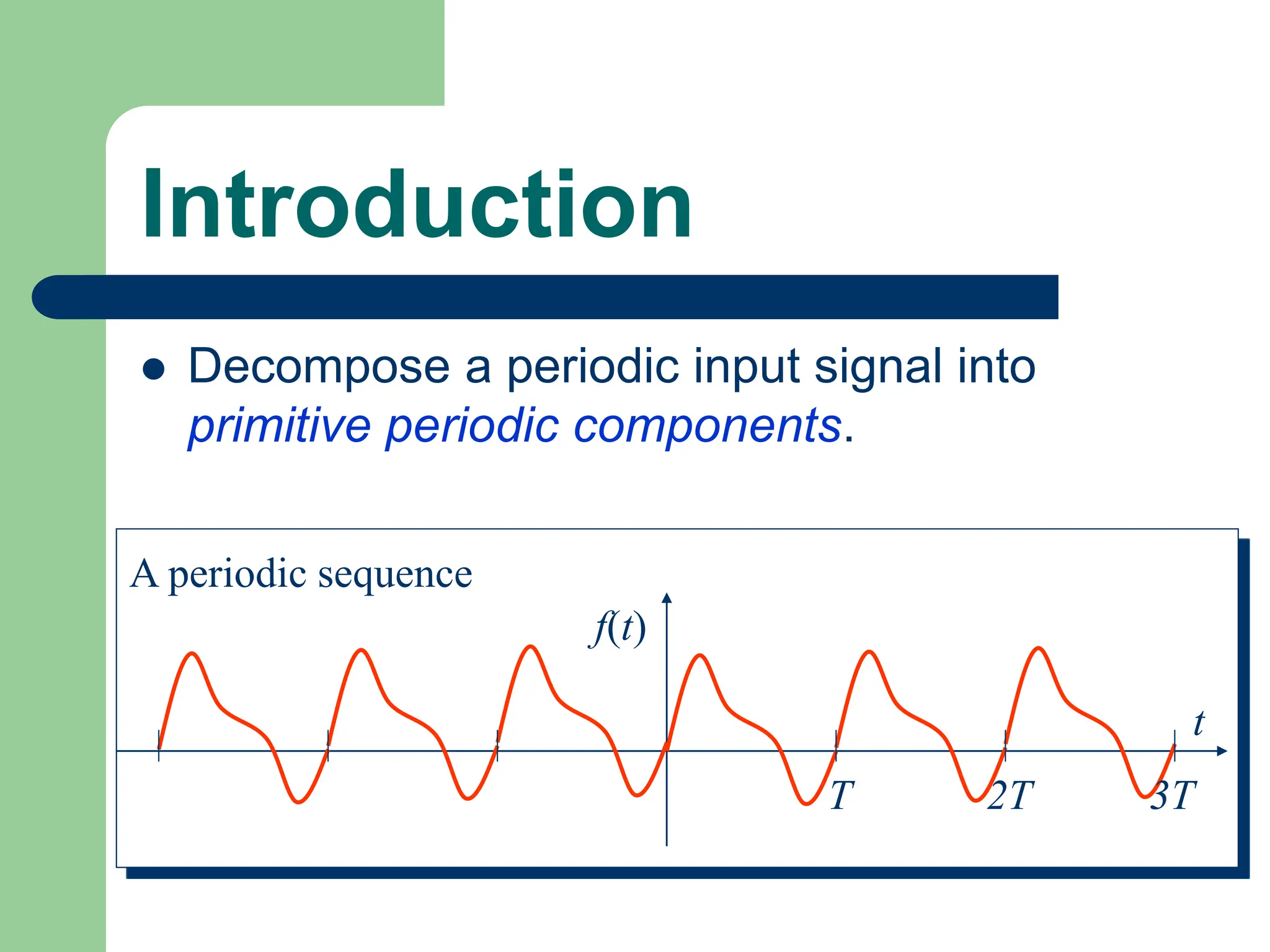
The document discusses the concept of Fourier series, introduced by Joseph Fourier, which allows periodic functions to be expressed as a sum of sines and cosines. It includes explanations of periodic functions, the mathematical formulation of Fourier series, and methods for analyzing periodic waveforms, including properties of symmetry and half-range expansions. Additionally, examples and proofs are provided to illustrate the decomposition of functions into basic periodic components.

1. Fourier Series
Present by
SUBHRANGSU
SEKHAR DEY
AMITY UNIVERSITY RAJASHAN
M.SC CHEMISTRY
DEPARTMENT OF
ASET

2. Joseph
Fourier(1768 -
1830)
Joseph Fourier(1768-1830), son of a
French taylor and friend of
nepolean,invented many examples of
expressions in trigonometric series in
connection with the problems of
conduction heat.His book entitled
“Theoric Analytique de le
Chaleur”(Analytical theory of heat)
published in 1822 is classical is the
theory of heat conduction for boundary
value problem.the fourier series comes
after his name for periodic function to be
expanded in trigonometric series.

3. Content
 Periodic Functions
 Fourier Series
 Analysis of Periodic Waveforms
● Half Range Series

4. Fourier Series
Periodic Functions

5. The Mathematic Formulation
 Any function that satisfies
( ) ( )
f t f t T
 
where T is a constant and is called the period
of the function.

6. Example:
4
cos
3
cos
)
(
t
t
t
f 
 Find its period.
)
(
)
( T
t
f
t
f 
 )
(
4
1
cos
)
(
3
1
cos
4
cos
3
cos T
t
T
t
t
t





Fact: )
2
cos(
cos 



 m

 m
T
2
3

 n
T
2
4

 m
T 6

 n
T 8

 24
T smallest T

7. Example:
t
t
t
f 2
1 cos
cos
)
( 


 Find its period.
)
(
)
( T
t
f
t
f 
 )
(
cos
)
(
cos
cos
cos 2
1
2
1 T
t
T
t
t
t 










 m
T 2
1


 n
T 2
2
n
m



2
1
2
1

 must be a
rational number

8. Example:
t
t
t
f )
10
cos(
10
cos
)
( 



Is this function a periodic one?





10
10
2
1 not a rational
number

9. Fourier Series
Fourier Series

10. Introduction
 Decompose a periodic input signal into
primitive periodic components.
A periodic sequence
T 2T 3T
t
f(t)

11. Synthesis
T
nt
b
T
nt
a
a
t
f
n
n
n
n




 





2
sin
2
cos
2
)
(
1
1
0
DC Part Even Part Odd Part
T is a period of all the above signals
)
sin(
)
cos(
2
)
( 0
1
0
1
0
t
n
b
t
n
a
a
t
f
n
n
n
n 



 





Let 0=2/T.

12. Decomposition
dt
t
f
T
a
T
t
t



0
0
)
(
2
0

,
2
,
1
cos
)
(
2
0
0
0


 

n
tdt
n
t
f
T
a
T
t
t
n

,
2
,
1
sin
)
(
2
0
0
0


 

n
tdt
n
t
f
T
b
T
t
t
n
)
sin(
)
cos(
2
)
( 0
1
0
1
0
t
n
b
t
n
a
a
t
f
n
n
n
n 



 






13. Proof
Use the following facts:
0
,
0
)
cos(
2
/
2
/
0 



m
dt
t
m
T
T
0
,
0
)
sin(
2
/
2
/
0 



m
dt
t
m
T
T








 n
m
T
n
m
dt
t
n
t
m
T
T 2
/
0
)
cos(
)
cos(
2
/
2
/
0
0








 n
m
T
n
m
dt
t
n
t
m
T
T 2
/
0
)
sin(
)
sin(
2
/
2
/
0
0
n
m
dt
t
n
t
m
T
T
and
all
for
,
0
)
cos(
)
sin(
2
/
2
/
0
0 




14. Example (Square Wave)
1
1
2
2
0
0 

 

dt
a

,
2
,
1
0
sin
1
cos
2
2
0
0








 n
nt
n
ntdt
an
,
6
,
4
,
2
0
,
5
,
3
,
1
/
2
)
1
cos
(
1
cos
1
sin
2
2
0
0











  

n
n
n
n
n
nt
n
ntdt
bn







 2 3 4 5
-
-2
-3
-4
-5
-6
f(t)
1

15. 1
1
2
2
0
0 

 

dt
a

,
2
,
1
0
sin
1
cos
2
2
0
0








 n
nt
n
ntdt
an
,
6
,
4
,
2
0
,
5
,
3
,
1
/
2
)
1
cos
(
1
cos
1
sin
2
1
0
0



















 

n
n
n
n
n
nt
n
ntdt
bn
 2 3 4 5
-
-2
-3
-4
-5
-6
f(t)
1
Example (Square Wave)











 
t
t
t
t
f 5
sin
5
1
3
sin
3
1
sin
2
2
1
)
(

16. 1
1
2
2
0
0 

 

dt
a

,
2
,
1
0
sin
1
cos
2
2
0
0








 n
nt
n
ntdt
an
,
6
,
4
,
2
0
,
5
,
3
,
1
/
2
)
1
cos
(
1
cos
1
sin
2
1
0
0



















 

n
n
n
n
n
nt
n
ntdt
bn
 2 3 4 5
-
-2
-3
-4
-5
-6
f(t)
1
Example (Square Wave)
-0.5
0
0.5
1
1.5











 
t
t
t
t
f 5
sin
5
1
3
sin
3
1
sin
2
2
1
)
(

17. Find the Fourier series for
In both cases note that we are integrating an odd function (x is
odd and cosine is even so the product is odd) over the
interval and so we know that both of these integrals will be
zero.
Example

18. Next here is the integral for
In this case we’re integrating an even function (x and sine are both
odd so the product is even) on the interval and so we can
“simplify” the integral as shown above. The reason for doing this
here is not actually to simplify the integral however. It is instead
done so that we can note that we did this integral back in the
Fourier sine series section and so don’t need to redo it in this
section. Using the previous result we get,

19. In this case the Fourier series is,

20. Fourier Series
Analysis of
Periodic Waveforms

21. Waveform Symmetry
 Even Functions
 Odd Functions
)
(
)
( t
f
t
f 

)
(
)
( t
f
t
f 



22. Decomposition
 Any function f(t) can be expressed as the
sum of an even function fe(t) and an odd
function fo(t).
)
(
)
(
)
( t
f
t
f
t
f o
e 

)]
(
)
(
[
)
( 2
1
t
f
t
f
t
fe 


)]
(
)
(
[
)
( 2
1
t
f
t
f
t
fo 


Even Part
Odd Part

23. Example







0
0
0
)
(
t
t
e
t
f
t
Even Part
Odd Part







0
0
)
(
2
1
2
1
t
e
t
e
t
f t
t
e








0
0
)
(
2
1
2
1
t
e
t
e
t
f t
t
o

24. Half-Wave Symmetry
)
(
)
( T
t
f
t
f 
 and  
2
/
)
( T
t
f
t
f 



25. Quarter-Wave Symmetry
Even Quarter-Wave Symmetry
T
T/2
T/2
Odd Quarter-Wave Symmetry
T
T/2
T/2

26. Hidden Symmetry
 The following is a asymmetry periodic function:
 Adding a constant to get symmetry property.
A
T
T
A/2
A/2
T
T

27. Fourier Coefficients of
Symmetrical Waveforms
 The use of symmetry properties simplifies the
calculation of Fourier coefficients.
– Even Functions
– Odd Functions
– Half-Wave
– Even Quarter-Wave
– Odd Quarter-Wave
– Hidden

28. 0
,
cos
)
(
2
cos
2
)
(
0
1
0








n
dx
l
x
n
x
f
l
a
where
l
x
n
a
a
x
f
l
n
n
n


HALF RANGE SERIES
COSINE SERIES
A function defined in can be expanded
as a Fourier series of period containing only
cosine terms by extending suitably in .
(As an even function)
)
(x
f
)
(x
f
)
,
0
( l
l
2
)
0
,
( l


29. SINE SERIES
A function defined in can be expanded
as a Fourier series of period containing
only sine terms by extending suitably in
[As an odd function]
1
,
sin
)
(
2
sin
)
(
0
1







n
dx
l
x
n
x
f
l
b
where
l
x
n
b
x
f
l
n
u
n


)
(x
f
)
(x
f
)
,
0
( l
).
0
,
( l

l
2

30. Expand in half range
(a) sine Series (b) Cosine series.
SOLUTION
(a)
Extend the definition of given function to that of
an odd function of period 4
i.e












2
0
;
0
2
;
)
(
x
x
x
x
x
f
2
0
,
)
( 

 x
x
x
f
Example of
Half Range Series

32. Here
dx
l
x
n
x
f
l
b
a
l
n
n



0
sin
)
(
2
0







n
n
x
n
n
x
n
x
dx
x
n
x
f
b
n
n
)
1
(
4
)
2
2
sin
(
1
)
2
2
cos
(
2
sin
)
(
2
2
2
0
2
2
2
2
0



















 

33. 2
sin
)
1
(
4
)
(
1
x
n
n
x
f
n
n








(b)
Extend the definition of given function to that of
an even function of period 4













2
0
;
0
2
;
)
(
x
x
x
x
x
f

35. dx
l
x
n
x
f
l
a
b
l
n
n



0
cos
)
(
2
0

 
0
;
1
)
1
(
4
)
2
2
cos
(
1
)
2
2
sin
(
2
cos
)
(
2
2
2
2
2
0
2
2
2
2
0



















 
n
n
n
x
n
n
x
n
x
dx
x
n
x
f
a
n
n







36.  

2
0
0 2
xdx
a
 
2
cos
1
)
1
(
4
1
)
(
1
2
2
x
n
n
x
f
n
n










37. Thank You