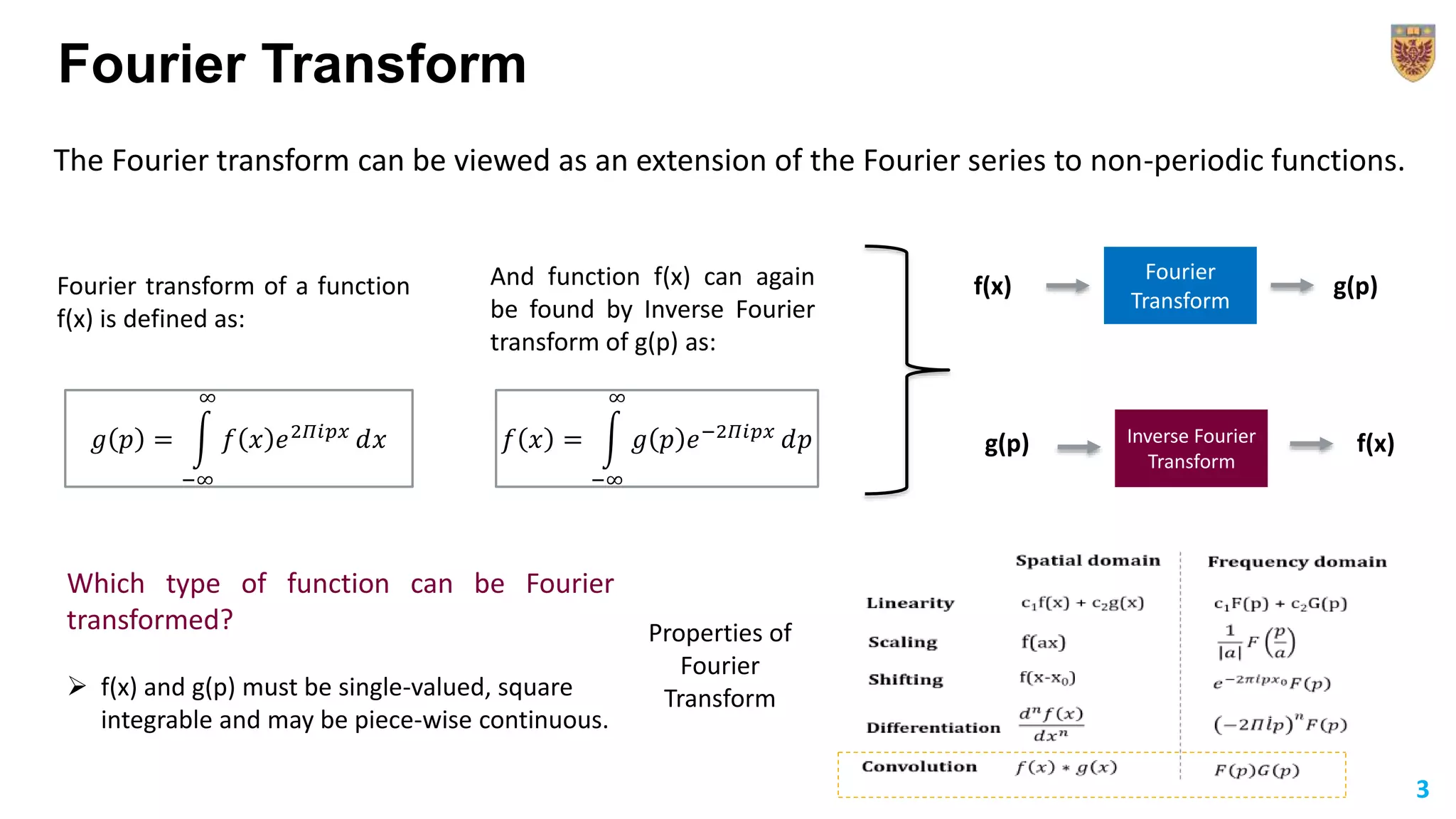
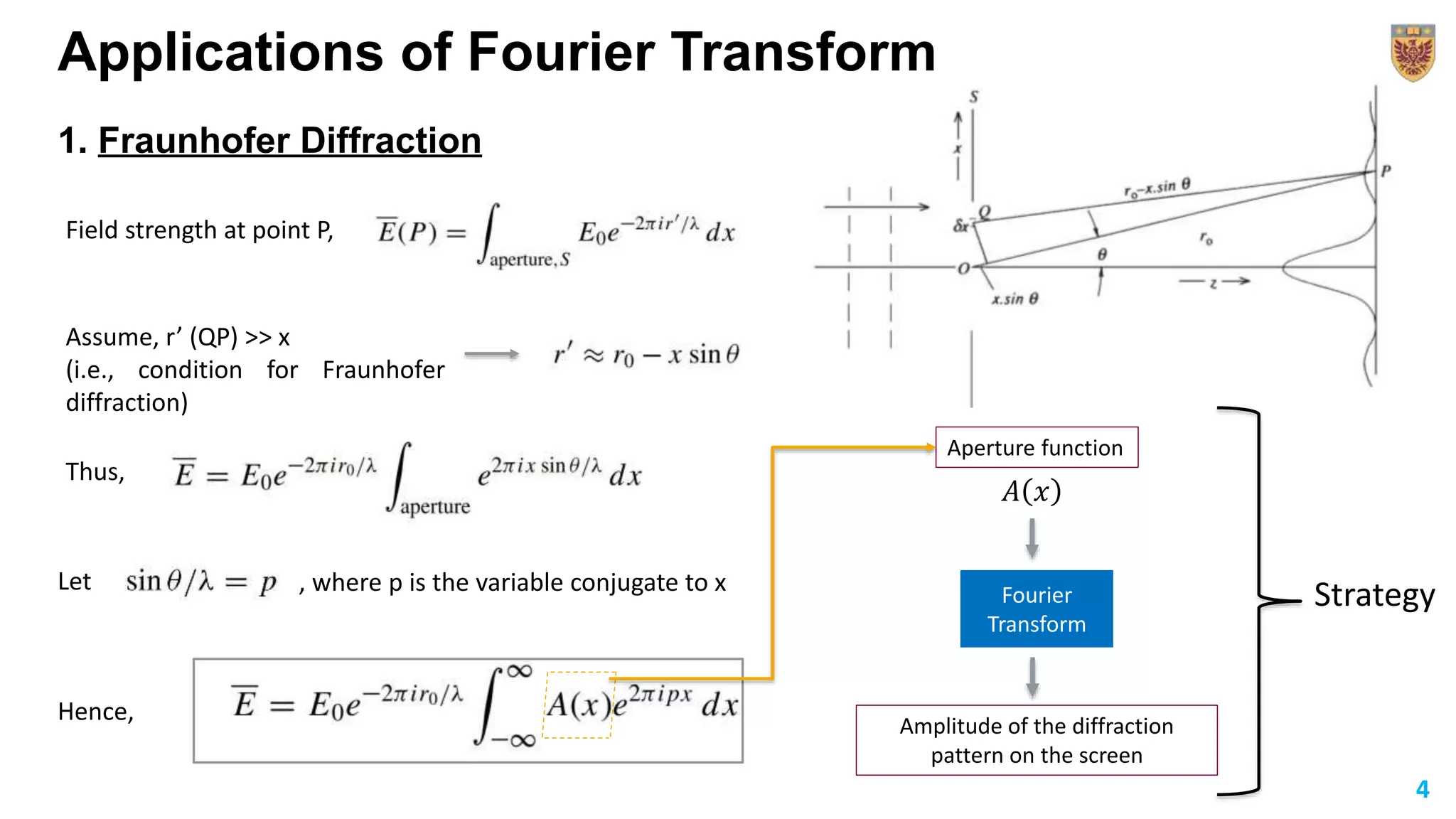
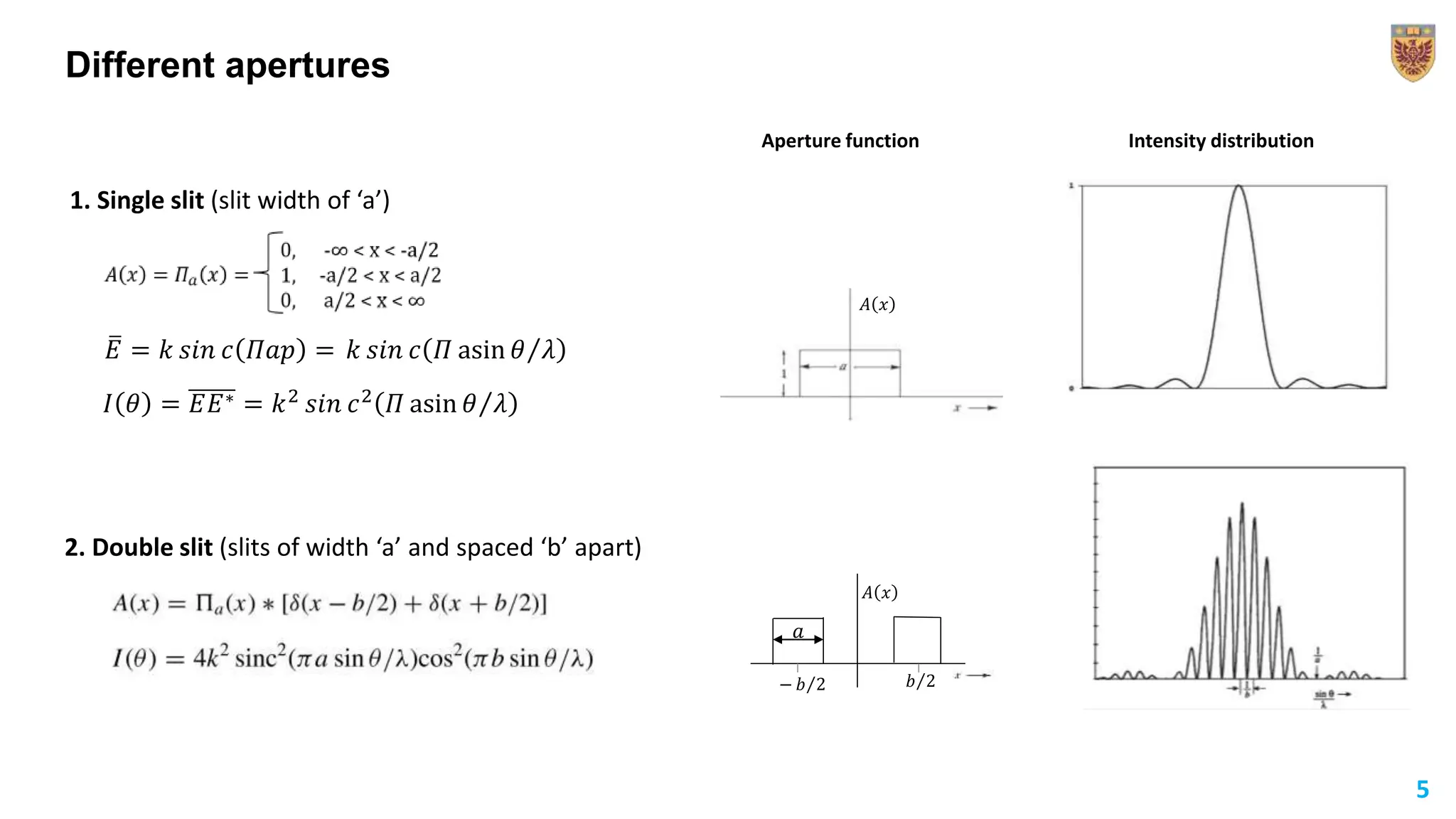
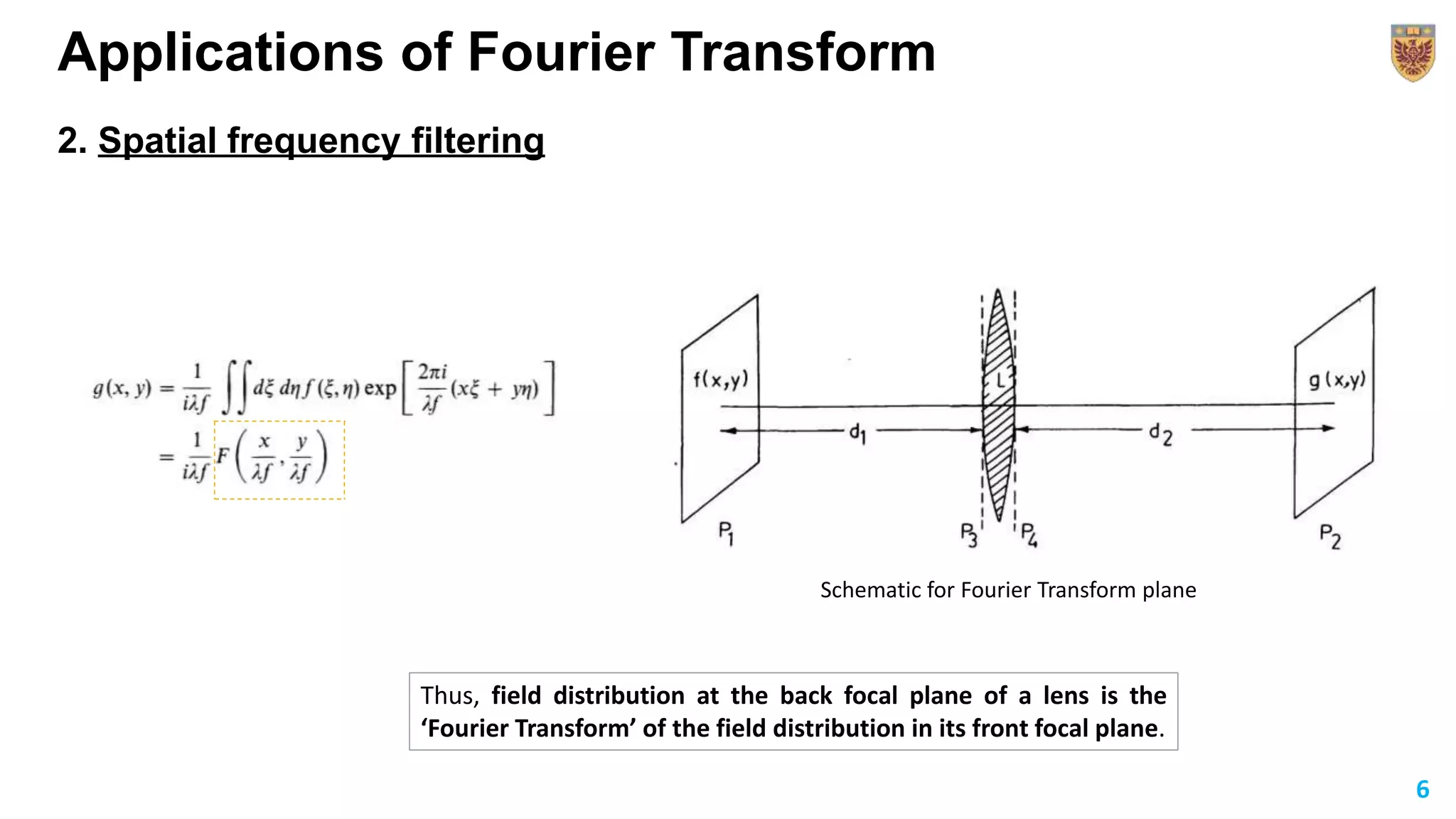
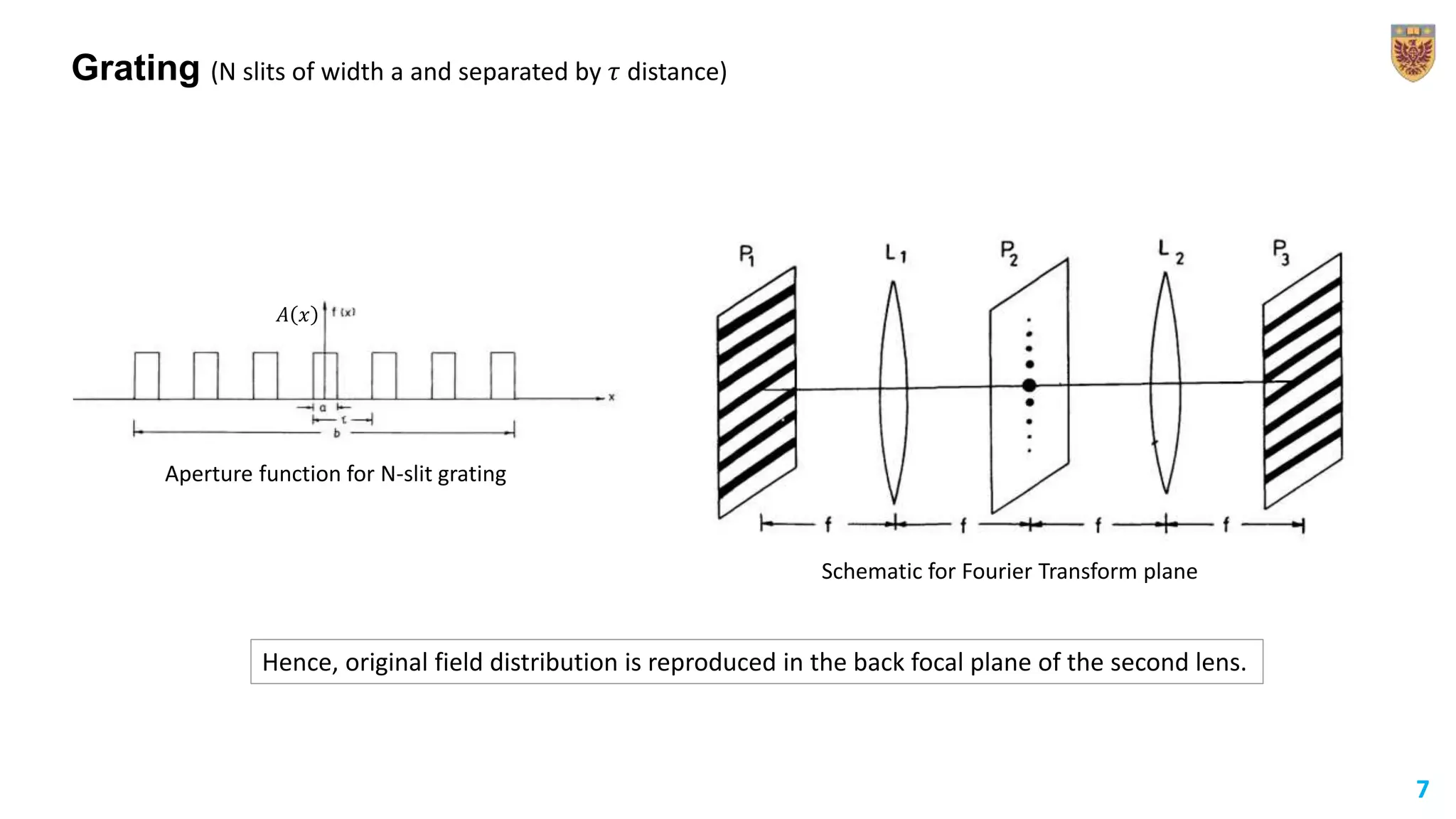
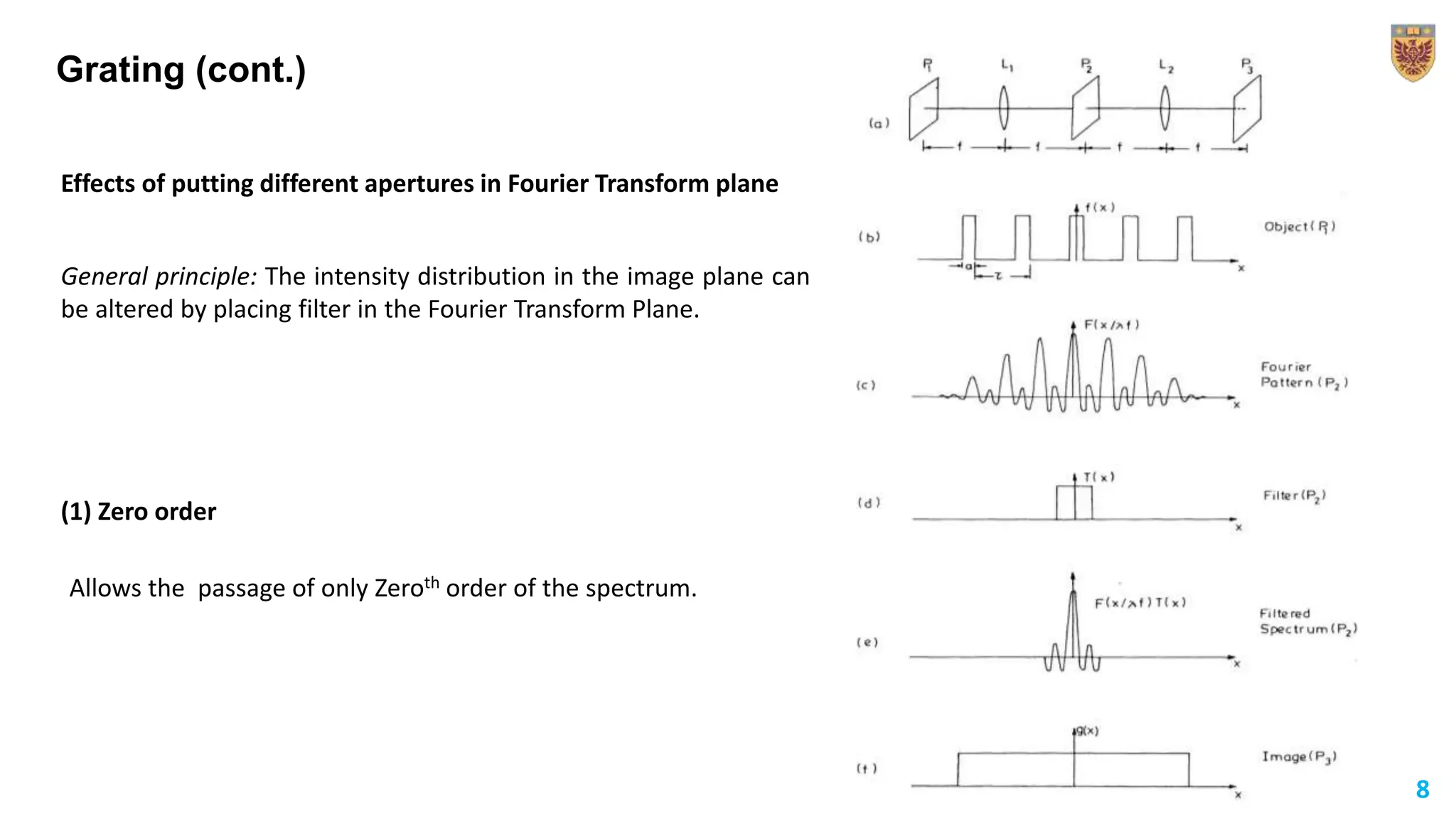
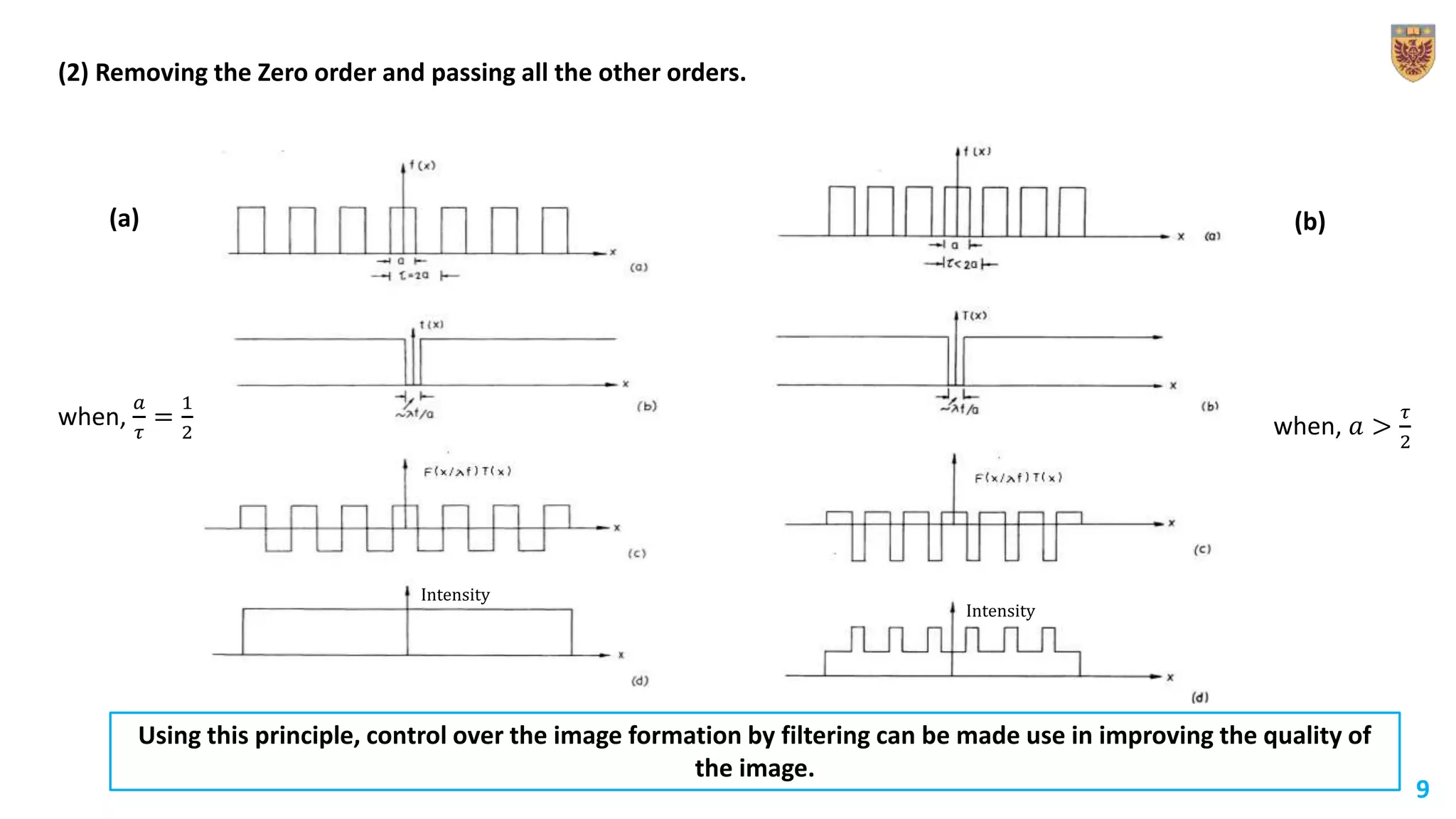
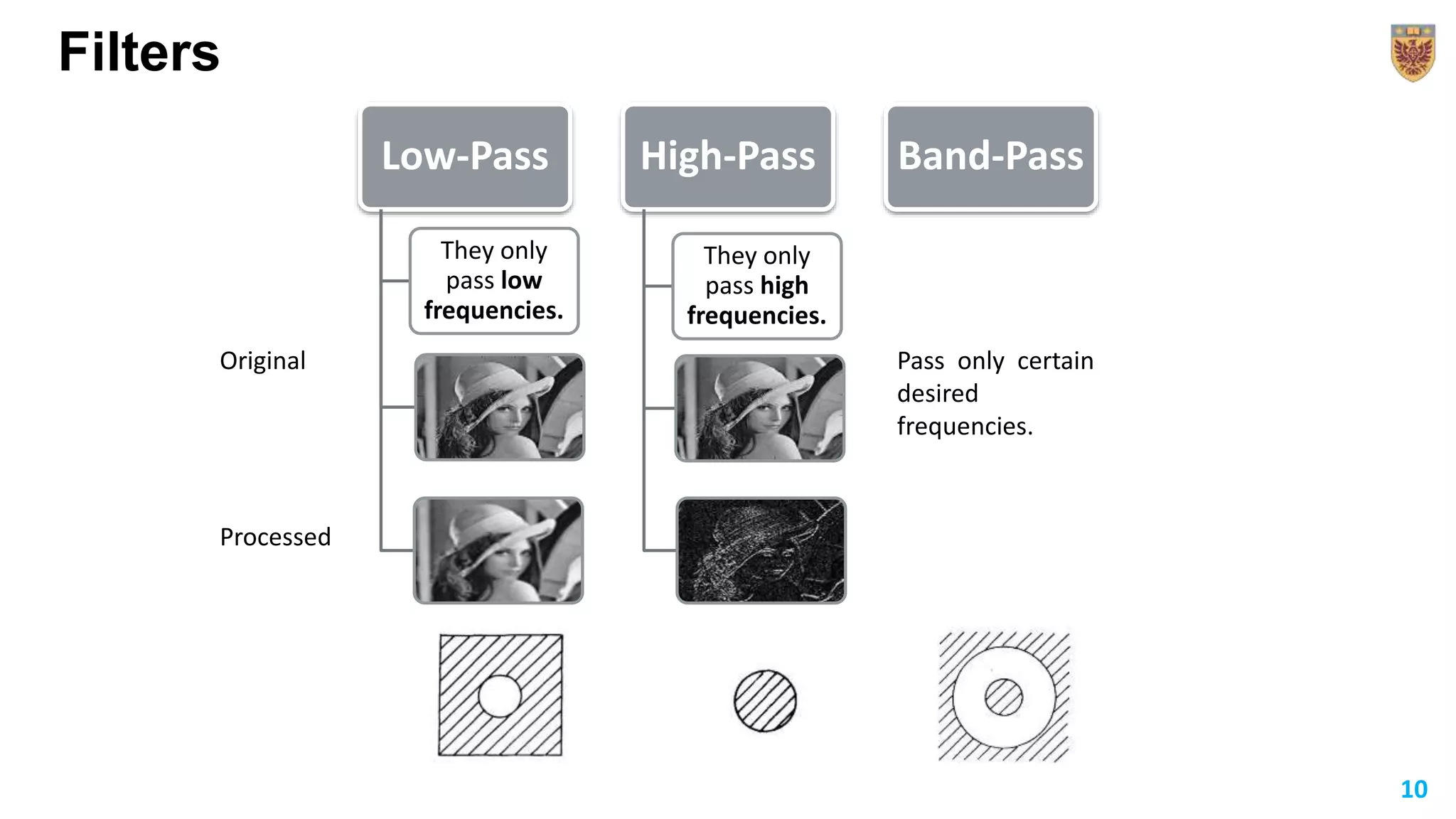
The document discusses the applications of Fourier transforms, extending the concept from Fourier series to non-periodic functions. It outlines the mathematical definitions, properties, and practical uses, such as in Fraunhofer diffraction and spatial frequency filtering. The document emphasizes how filtering in the Fourier transform plane can enhance image quality by controlling intensity distributions.