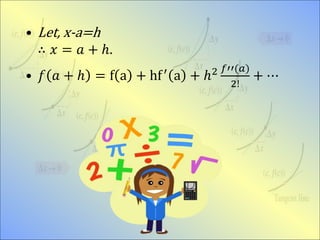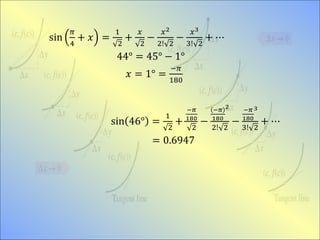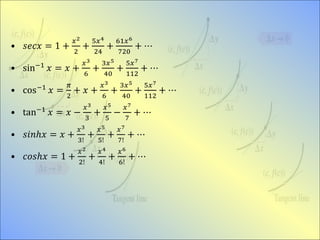This document discusses Taylor and Maclaurin series. It provides examples of expanding functions using these series, including expanding polynomials, trigonometric functions like sin and cos, and the natural log function. Standard expansions are also listed for common functions using Maclaurin series, such as e^x, ln(1+x), sin(x), and tanh(x).

1. GujaratPower EngineeingAndResearch
Institute
Sub :- Calculus
Topic :- Taylor’s and Maclaurin’s
Series
Nikhil Patel (161040119038)
Parth Patel (161040119040)
Smit Patel (161040119043)
Amit Prajapati (161040119047)
Created By :-Guided By :-
Prof. Janki Gajjar

2. Details
1) Taylor’s Series
I. Definition
II. Examples
2) Maclaurin’s Series
I. Definition
II. Examples
3) Standard Expand of Maclarin’s Series

3. Taylor’s Series
• Definition :- Let f be a function such that it
is infinitely many time differentiable in some
open interval I at some internal point x=a.
then the Taylor’s series generated by f at x=a
is,
𝑛=0
∞
𝑓 𝑛
(𝑎)
𝑛!
(𝑥 − 𝑎) 𝑛
= f a + f′
a x − a + f′′
a
𝑥 − 𝑎 2
2!
+ ⋯

4. • Let, x-a=h
∴ 𝑥 = 𝑎 + ℎ.
• 𝑓 𝑎 + ℎ = f a + hf′
a + ℎ2 𝑓′′(𝑎)
2!
+ ⋯

5. EXAMPLES
(1) Expand 𝑓 𝑥 = 𝑥4 − 11𝑥3 + 43𝑥2 − 60𝑥 + 14 in powers of x-3.
Ans. Hear x-a=x-3
So,a=3
We have to fine series about the point a=3.
𝑓 𝑥 = 𝑥4 − 11𝑥3 + 43𝑥2 − 60𝑥 + 14 ⇒ f 3 = 5
𝑓′ 𝑥 = 4𝑥3 − 33𝑥2 + 86𝑥 − 60 ⇒ 𝑓′ 3 = 9
𝑓′′ 𝑥 = 12𝑥2 − 66𝑥 + 86 ⇒ 𝑓′′ 3 = −4
𝑓′′′ 𝑥 = 24𝑥 − 66 ⇒ 𝑓′′′ 3 = 6
𝑓 𝑖𝑣
𝑥 = 24 ⇒ 𝑓 𝑖𝑣
3 = 24

6. We put this value In Taylor’s series, We get
𝑓 𝑥 = 5 + 9 𝑥 − 3 − 4
𝑥 − 3 2
2!
+ 6
𝑥 − 3 3
3!
+ 24
(𝑥 − 3)4
4!
= 5 + 9 𝑥 − 3 − 2 𝑥 − 3 2 + 𝑥 − 3 3 + (𝑥 − 3)4

7. (2) Using Taylor’s theorem find value of 25.15.
Ans.
𝑓 𝑎 + ℎ = 25.15
∴ 25.15 = 25 + 0.15
∴ 𝑎 = 25 ℎ = 0.15
𝑓 𝑥 = 𝑥
1
2 ⇒ 𝑓 25 = 5
𝑓′ 𝑥 =
1
2
∗
1
𝑥2 . ⇒ 𝑓′ 25 =
1
2
∗
1
5
𝑓′′ 𝑥 =
1
2
∗
−1
2
∗
1
𝑥
3
2
⇒ 𝑓′′ 25 =
−1
4
∗
1
53
𝑓′′′ 𝑥 =
−1
4
∗
−3
2
∗
1
𝑥
5
2
⇒ 𝑓′′′ 25 =
3
8
∗
1
55

8. 𝑓 𝑎 + ℎ = f a + hf′ a + ℎ2 𝑓′′(𝑎)
2!
+ ⋯
25.15 = 5 +
0.15
2
∗
1
5
−
0.15 2
2!∗4
∗
1
53 +
0.15 3∗3
3!∗8
∗
1
55 + ⋯

9. (3) Expand sin
𝜋
4
+ 𝑥 in power of 𝑥.Hence find the value of
𝑠𝑖𝑛44°.
Ans:
sin(
𝜋
4
+ 4)
let 𝑎 =
𝜋
4
𝑓 𝑥 = 𝑐𝑜𝑠𝑥 ⇒ 𝑓
𝜋
4
=
−1
2
𝑓′ 𝑥 = 𝑐𝑜𝑠𝑥 ⇒ 𝑓′ 𝜋
4
=
1
2
𝑓′′ 𝑥 = −𝑠𝑖𝑛𝑥 ⇒ 𝑓′′ 𝜋
4
= −
1
2
𝑓′′′ 𝑥 = −𝑐𝑜𝑠𝑥 ⇒ 𝑓′′′ 𝜋
4
=
−1
2
𝑓 𝑎 + ℎ = 𝑓 𝑎 + ℎ𝑓′ 𝑎 +
ℎ
2!
2
𝑓′′ 𝑎 + ⋯

10. sin
𝜋
4
+ 𝑥 =
1
2
+
𝑥
2
−
𝑥2
2! 2
−
𝑥3
3! 2
+ ⋯
44° = 45° − 1°
𝑥 = 1° =
−𝜋
180
sin 46° =
1
2
+
−𝜋
180
2
−
−𝜋
180
2
2! 2
−
−𝜋
180
3
3! 2
+ ⋯
= 0.6947

11. Maclaurin’s Series
• Definition :- Let f be a function such that it
has derivatives of all orders at x=0. then the
Maclaurin’s series generated by f is,
𝑛=0
∞
𝑓 𝑛
(0)
𝑛!
(𝑥 − 0) 𝑛 = f 0 + f′ 0 x + f′′ 0
𝑥 2
2!
+ ⋯

12. EXAMPLES
(1) Find a Maclaurin’s series of log 𝑠𝑖𝑛𝑥.
𝑓 𝑥 = log 1 − 𝑥 ⇒ 𝑓 0 = log 1 = 0
𝑓′ 𝑥 =
−1
1 − 𝑥
⇒ 𝑓′ 0 = −1
𝑓′′ 𝑥 =
−1
(1 − 𝑥)2
⇒ 𝑓′′ 0 = −1
𝑓′′′
𝑥 =
−2
(1 − 𝑥)3 ⇒ 𝑓′′′
0 = −2
𝑓 𝑖𝑣
𝑥 =
−6
(1 − 𝑥)4 ⇒ 𝑓 𝑖𝑣
0 = −6
We put this value in Maclaurin’s series we get,
ln 1 − 𝑥 = −𝑥 −
𝑥2
2
−
𝑥3
3
−
𝑥4
4
− ⋯

13. (2) Obtain a Maclaurin’s series for f x = 𝑐𝑜𝑠ℎ𝑥.
Ans.
Here,
𝑓 𝑥 = 𝑐𝑜𝑠ℎ𝑥 ⇒ 𝑓 0 =
1
𝑓′
𝑥 = 𝑠𝑖𝑛ℎ𝑥 ⇒ 𝑓′
0 = 0
𝑓′′
𝑥 = 𝑐𝑜𝑠ℎ𝑥 ⇒ 𝑓′′
0 = 1
𝑓′′′
𝑥 = 𝑠𝑖𝑛ℎ𝑥 ⇒ 𝑓′′′
0 = 0
𝑓 𝑖𝑣
𝑥 = 𝑐𝑜𝑠ℎ𝑥 ⇒ 𝑓 𝑖𝑣
0 = 1
We put this value in Maclaurin’s series we get
𝑓 𝑥 = 𝑐𝑜𝑠ℎ𝑥 = 1 +
𝑥2
2!
+
𝑥4
4!
+ ⋯

14. (3) Find Maclaurins’s series of
1
1+𝑥
.
Ans.
Here,
𝑓 𝑥 =
1
1+𝑥
⇒ f 0 = 1
𝑓′ 𝑥 =
−1
(1+𝑥)2 ⇒ f′ 0 = −1
𝑓′′
𝑥 =
2
(1+𝑥)3 ⇒ f′′
0 = 2
𝑓′′′
𝑥 =
−6
(1+𝑥)4 ⇒ f′′′
0 = −6

15. We put this value in Maclaurin’s series we get,
𝑓 𝑥 =
1
1+𝑥
= 1 + −1 𝑥 + 2
𝑥2
2!
+ −6
𝑥3
3!
+ ⋯
∴
1
1+𝑥
= 1 − 𝑥 + 𝑥2
− 𝑥3
+ ⋯

16. Standard Expanssion of
Maclaurin’s series
• 𝑒 𝑥 = 1 + 𝑥 +
𝑥2
2!
+
𝑥3
3!
+ ⋯
• 𝑒−𝑥
= 1 − 𝑥 +
𝑥2
2
−
𝑥3
3
+ ⋯
• ln 1 + 𝑥 = 𝑥 −
𝑥2
2
+
𝑥3
3
−
𝑥4
4
+ ⋯
• ln 1 − 𝑥 = −𝑥 −
𝑥2
2
−
𝑥3
3
−
𝑥4
4
− ⋯
• 𝑙𝑛
(1+𝑥)
(1−𝑥)
= 2𝑥 +
2
3
𝑥3 +
2
5
𝑥5 + ⋯
• 𝑠𝑖𝑛𝑥 = 𝑥 −
𝑥3
3!
+
𝑥5
5!
−
𝑥7
7!
+ ⋯
• 𝑐𝑜𝑠𝑥 = 1 −
𝑥2
2!
+
𝑥4
4!
−
𝑥6
6!
+ ⋯
• 𝑡𝑎𝑛𝑥 = 𝑥 +
𝑥3
3
+
2𝑥5
15
+
17𝑥7
315
+
62𝑥9
2835
+ ⋯

17. • 𝑠𝑒𝑐𝑥 = 1 +
𝑥2
2
+
5𝑥4
24
+
61𝑥6
720
+ ⋯
• sin−1
𝑥 = 𝑥 +
𝑥3
6
+
3𝑥5
40
+
5𝑥7
112
+ ⋯
• cos−1
𝑥 =
𝜋
2
+ 𝑥 +
𝑥3
6
+
3𝑥5
40
+
5𝑥7
112
+ ⋯
• tan−1 𝑥 = 𝑥 −
𝑥3
3
+
𝑥5
5
−
𝑥7
7
+ ⋯
• 𝑠𝑖𝑛ℎ𝑥 = 𝑥 +
𝑥3
3!
+
𝑥5
5!
+
𝑥7
7!
+ ⋯
• 𝑐𝑜𝑠ℎ𝑥 = 1 +
𝑥2
2!
+
𝑥4
4!
+
𝑥6
6!
+ ⋯