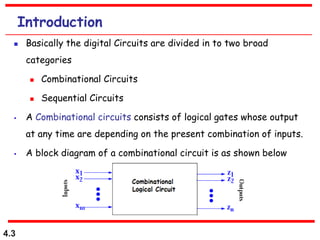
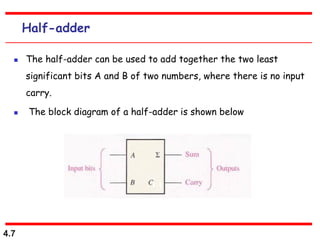
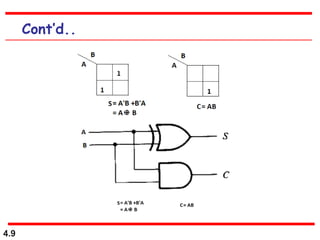
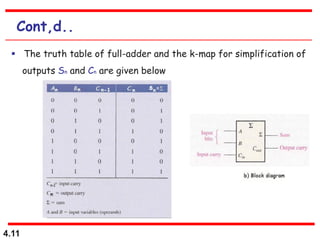
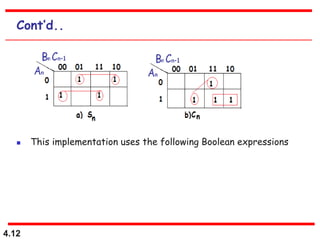
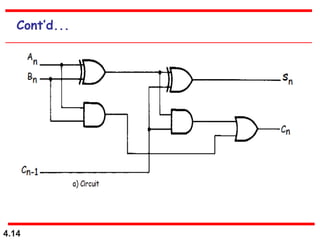
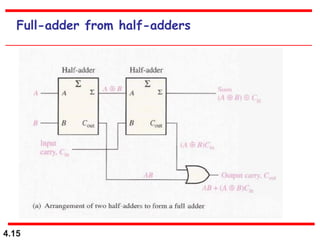
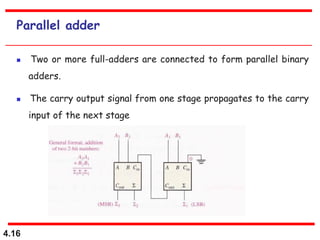
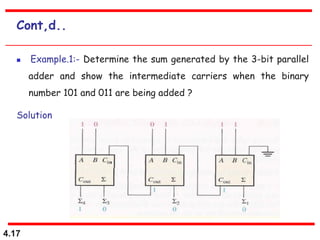
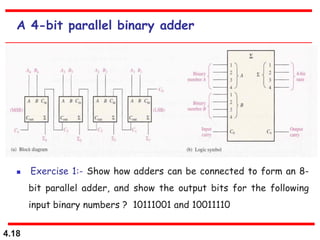
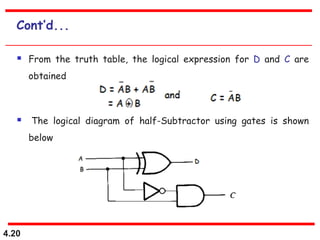
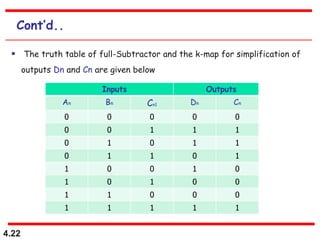
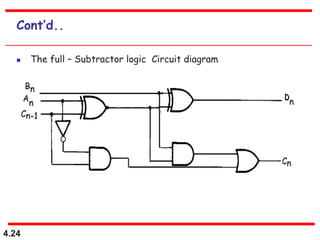
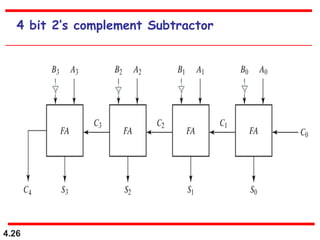
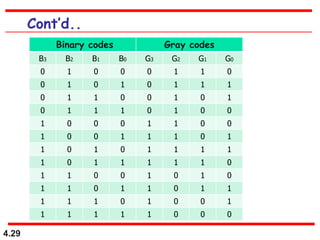
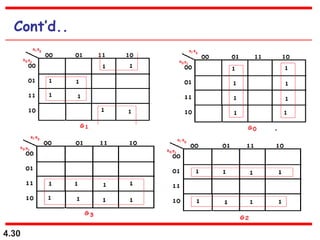
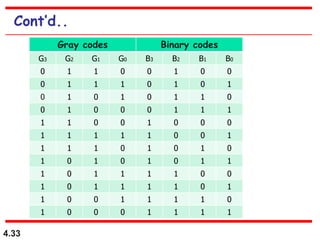
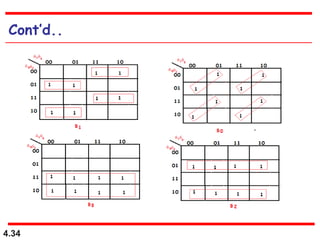
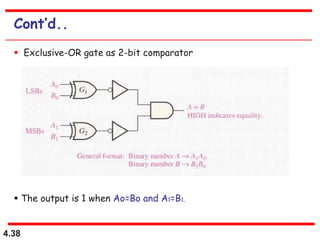
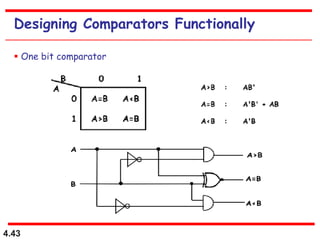
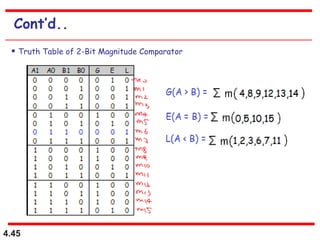
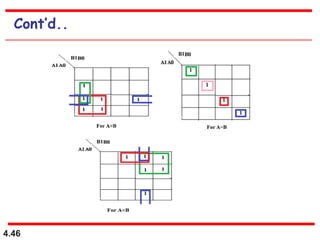
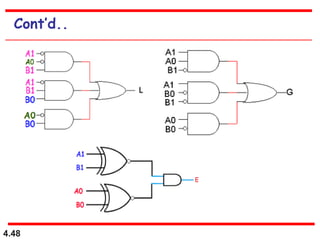
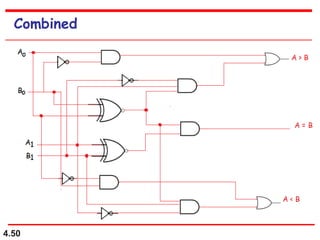
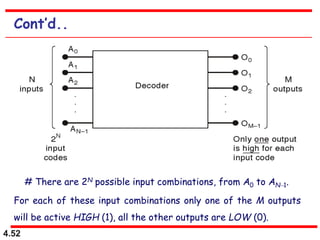
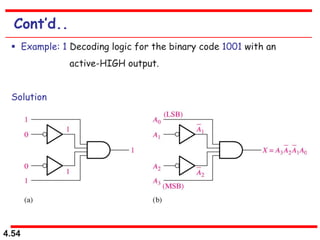
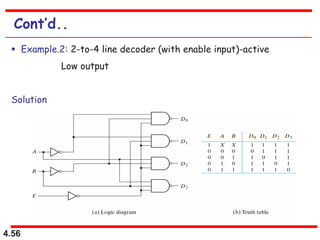
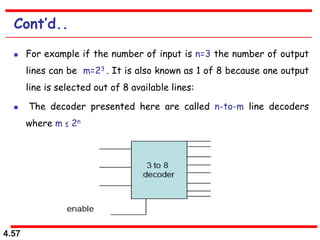
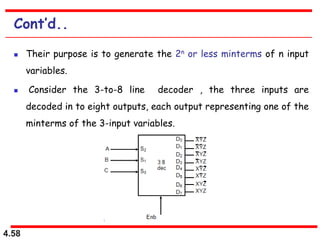
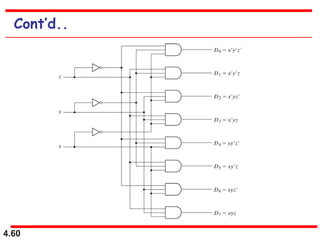
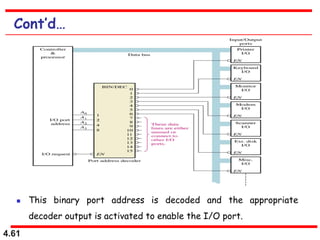
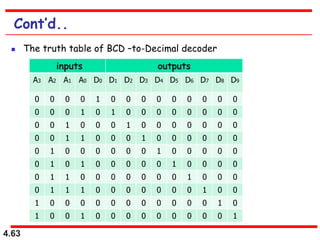
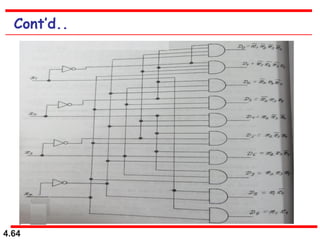
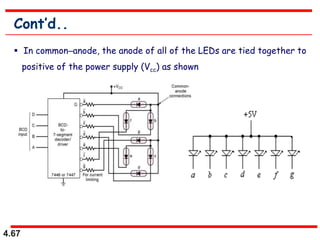
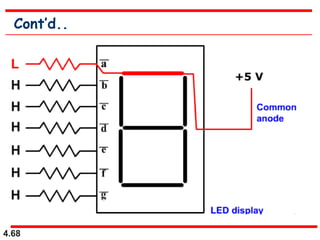
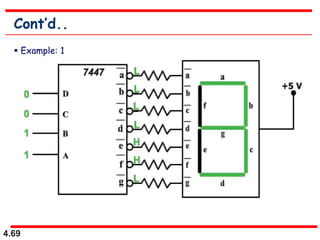
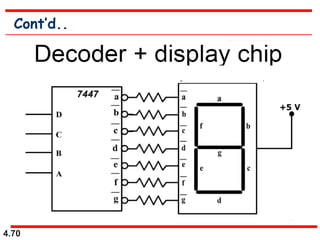
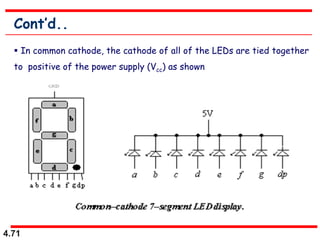
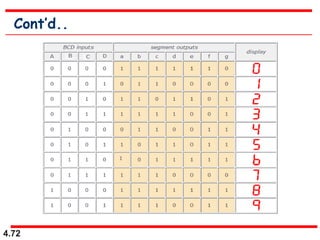
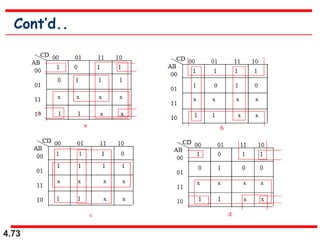
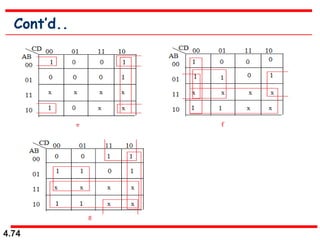
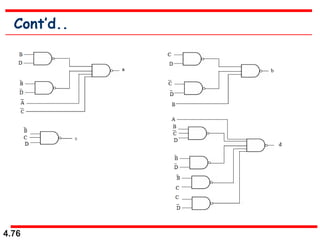
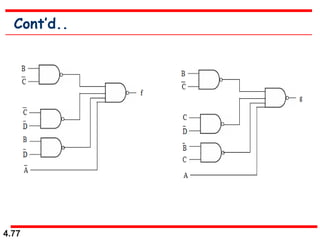
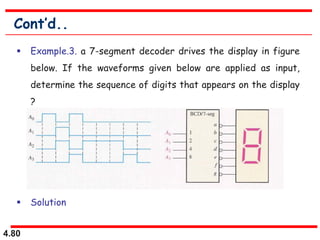
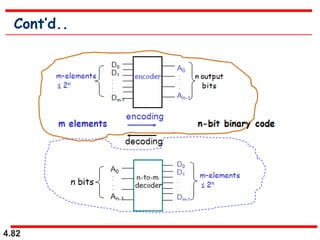
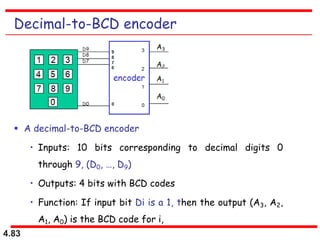
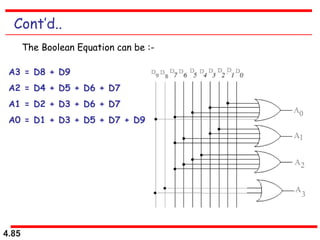
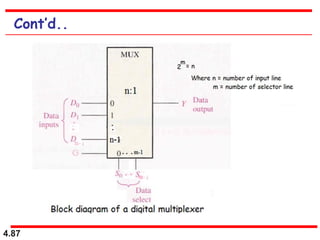
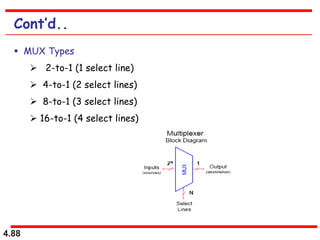
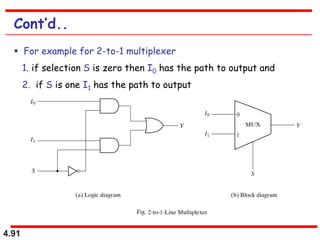
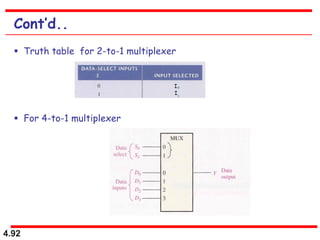
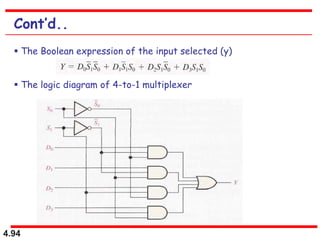
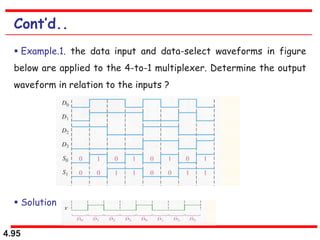
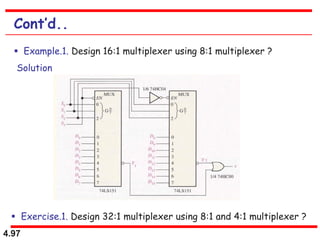
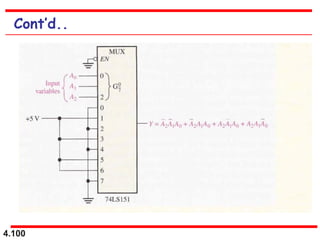
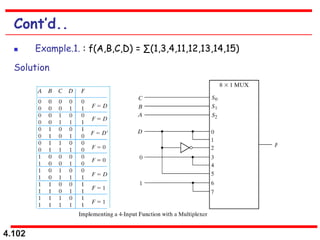
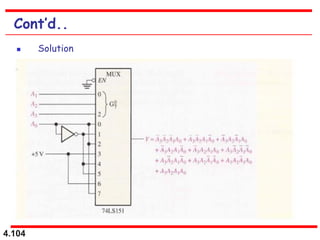
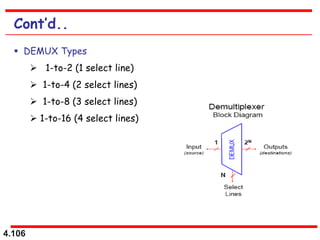
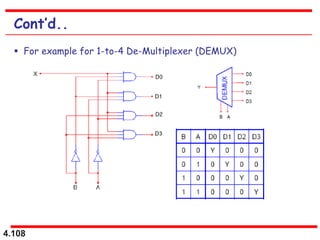
This document discusses combinational logic circuits. It begins with an introduction to combinational circuits and their characteristics. It then covers various types of combinational logic circuits including adders, subtractors, encoders, decoders, comparators, and multiplexers. For each circuit type, it provides explanations of how they work and examples of their logic designs and truth tables. The overall purpose is to explain the design and implementation of common combinational logic circuits.