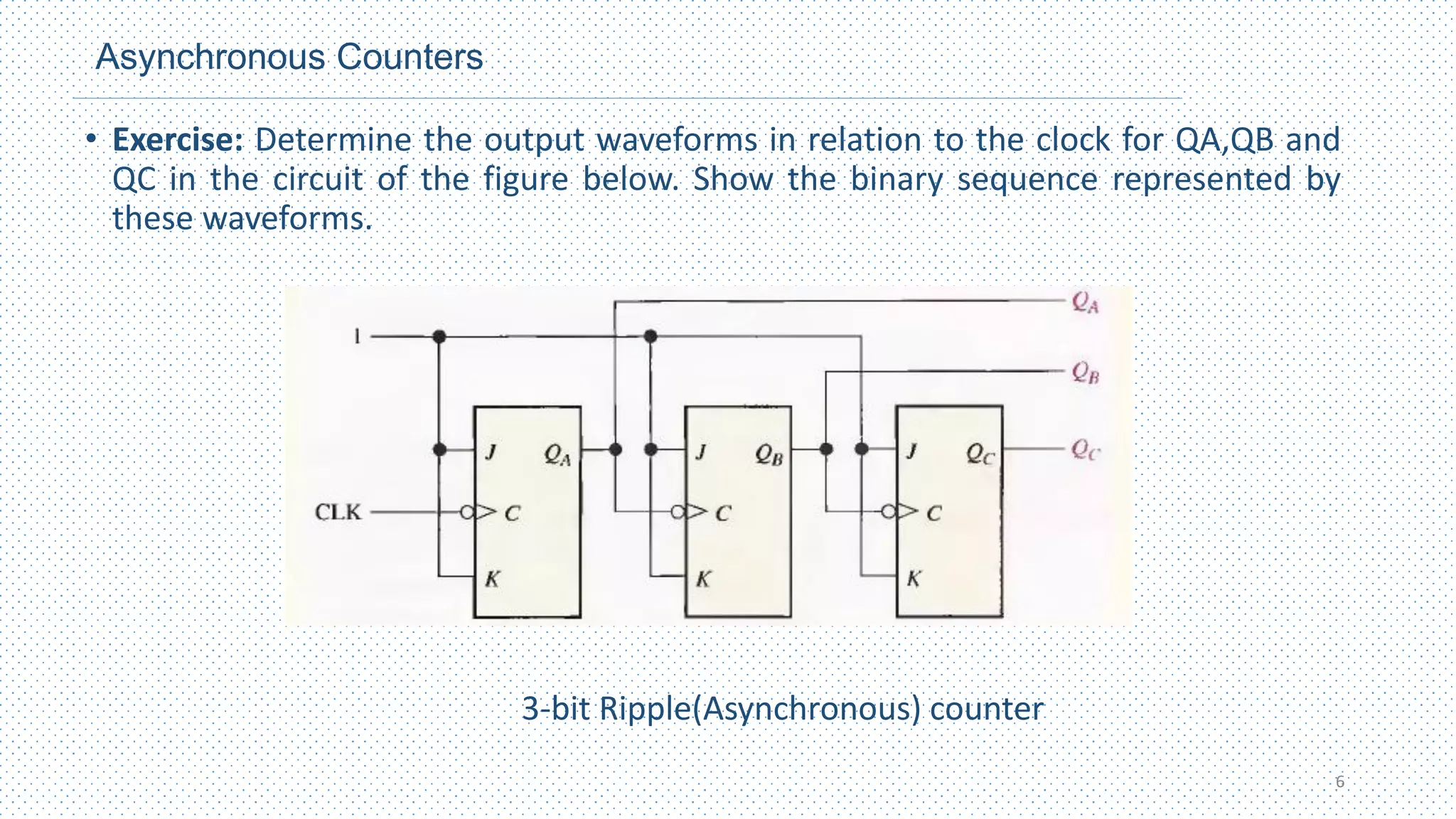
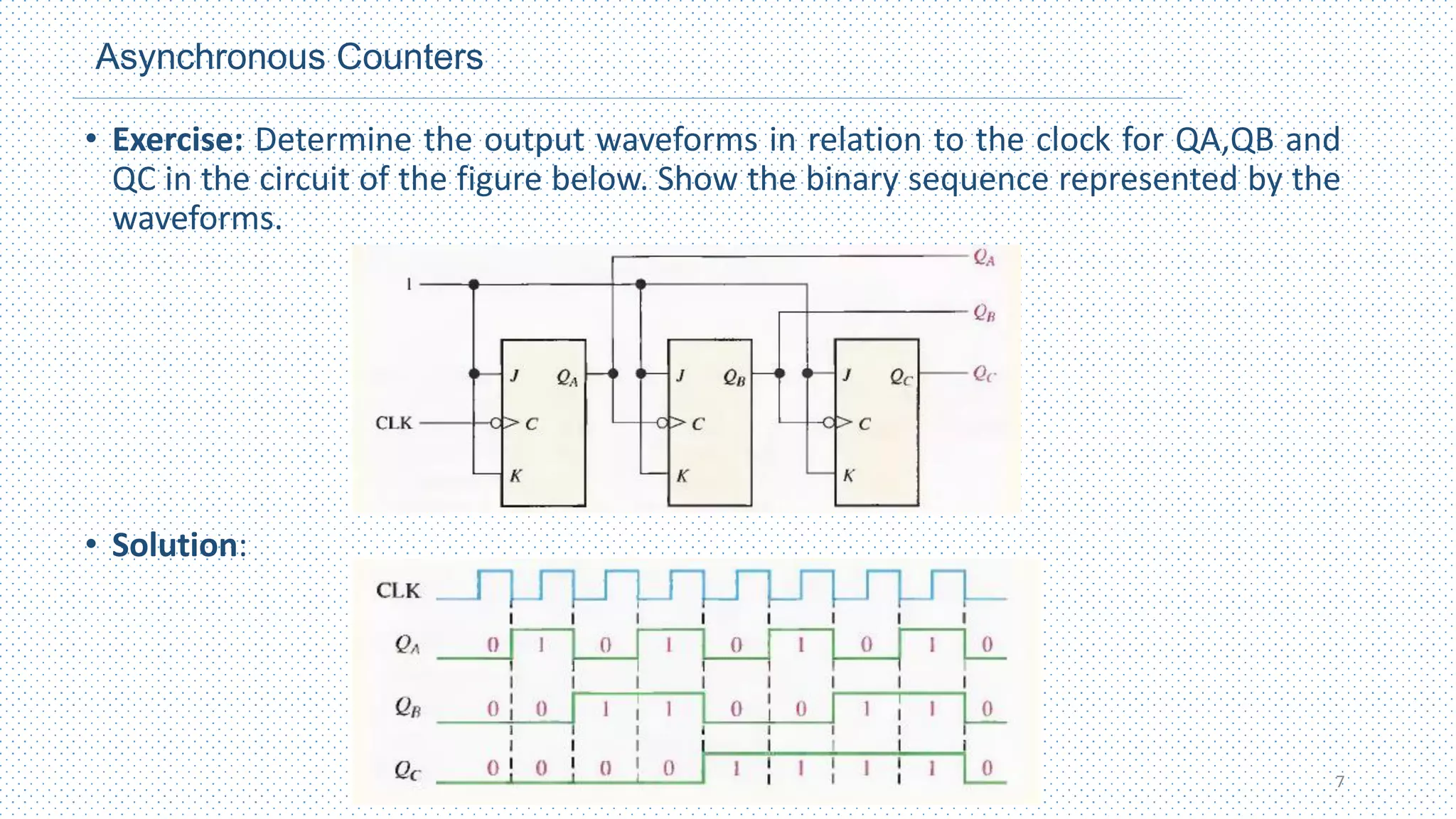
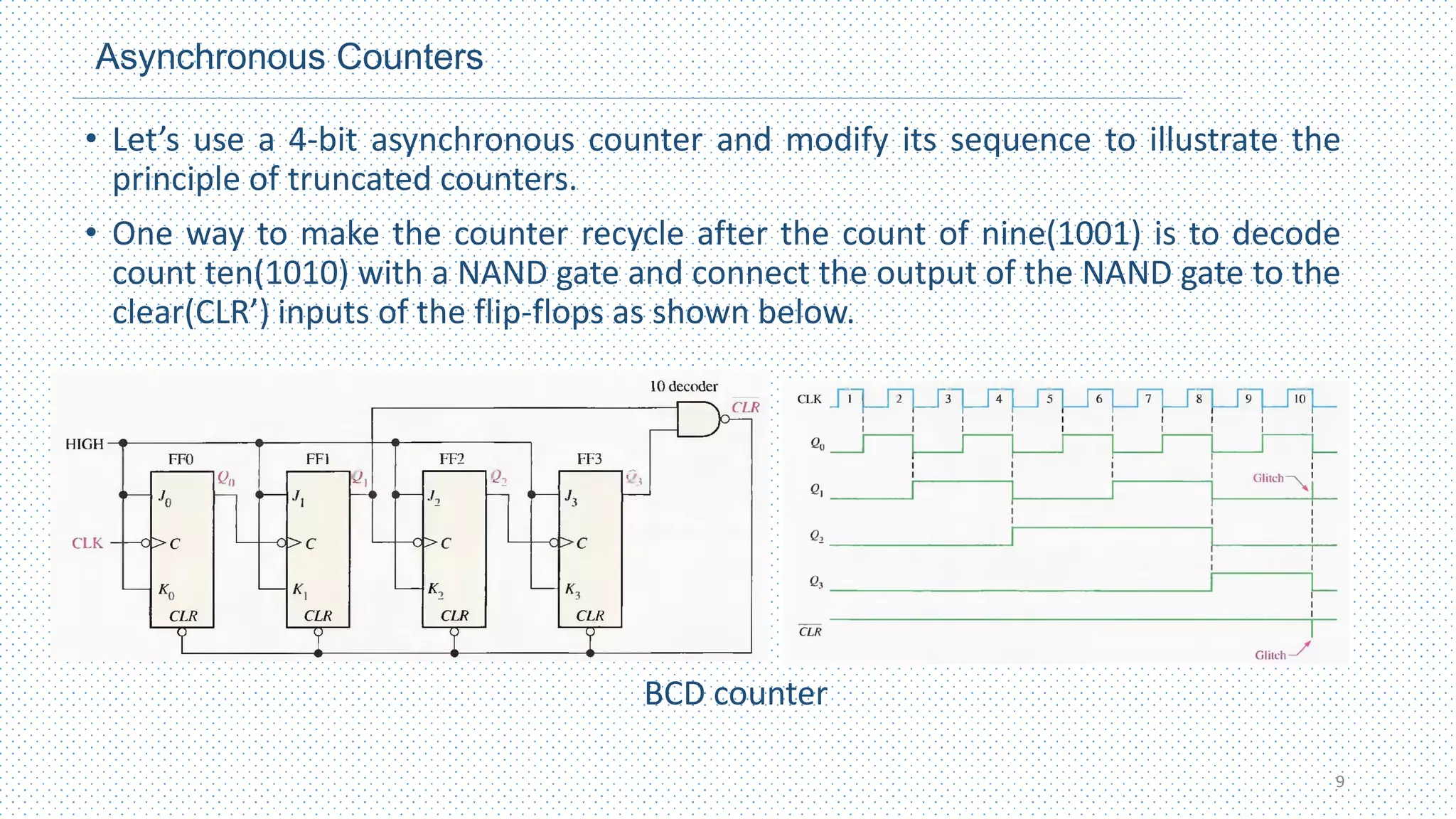
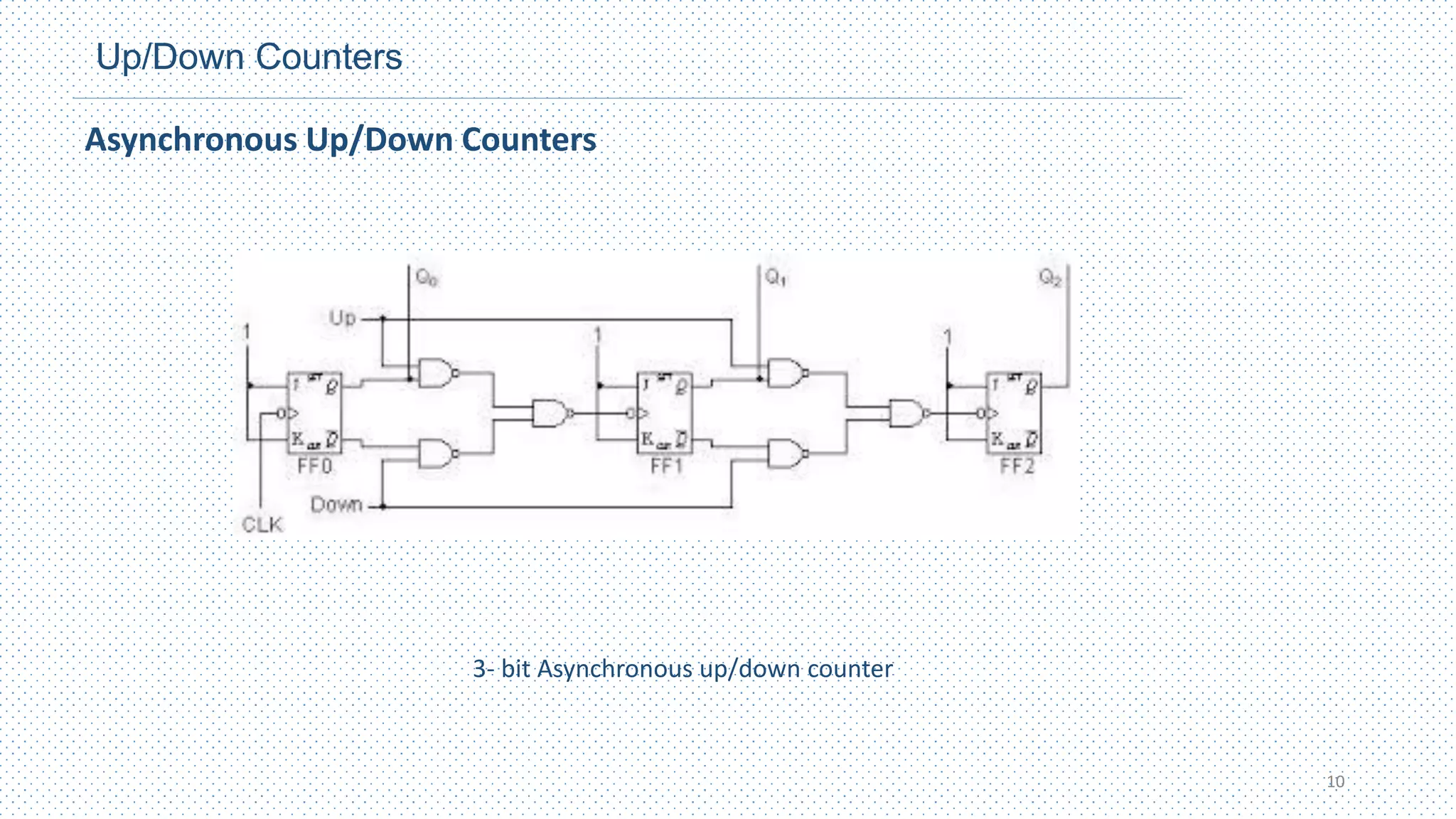
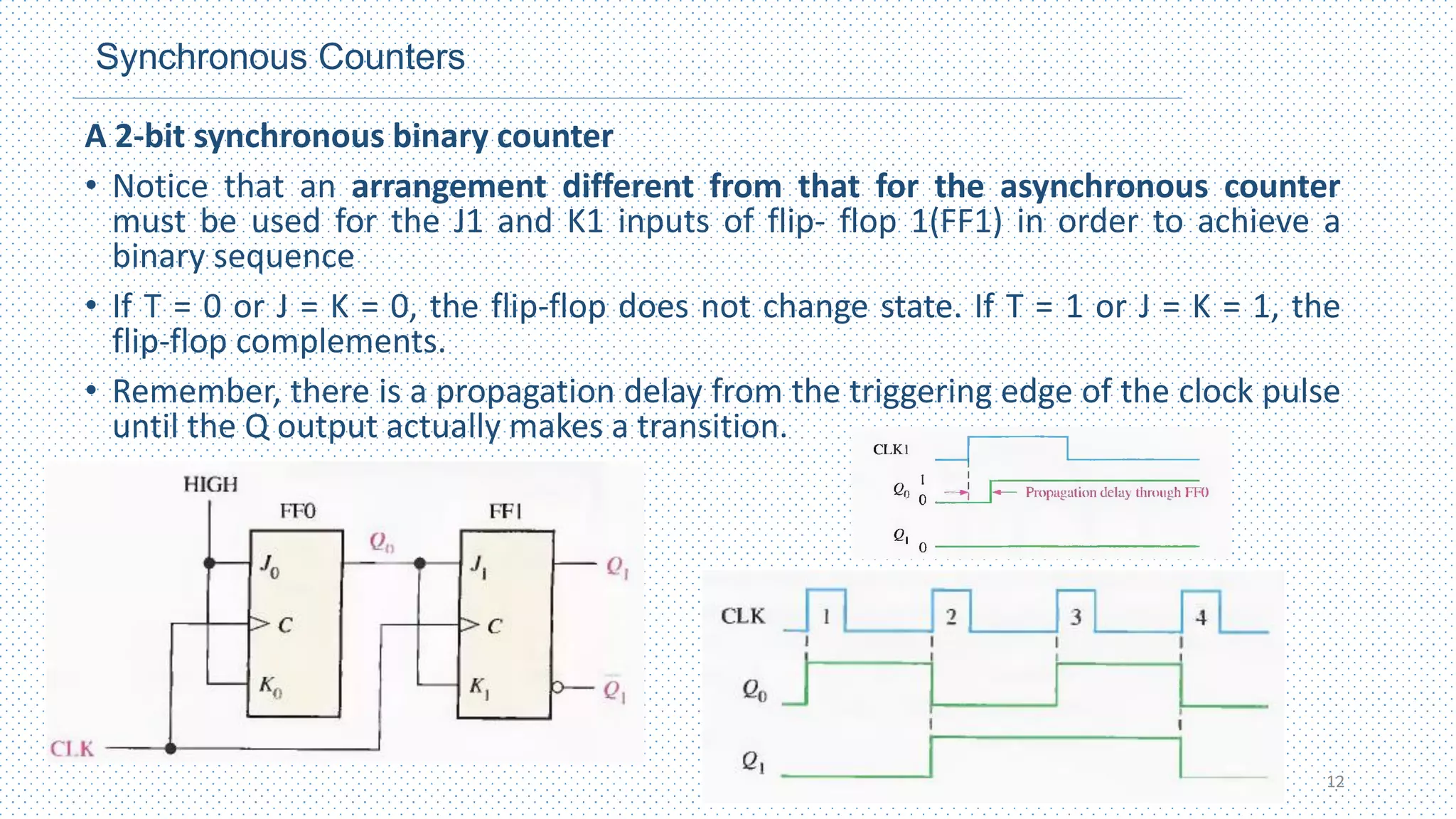
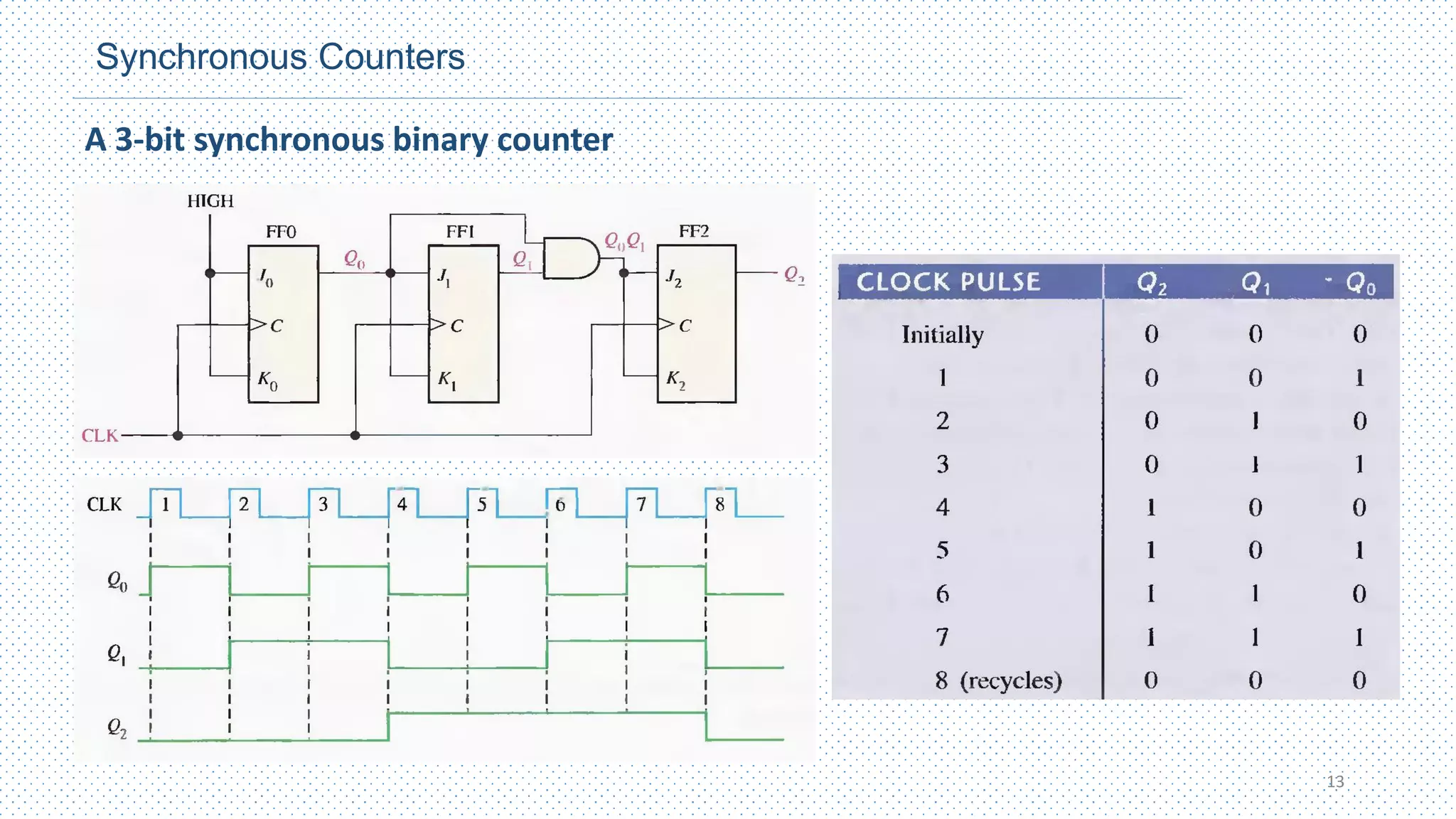
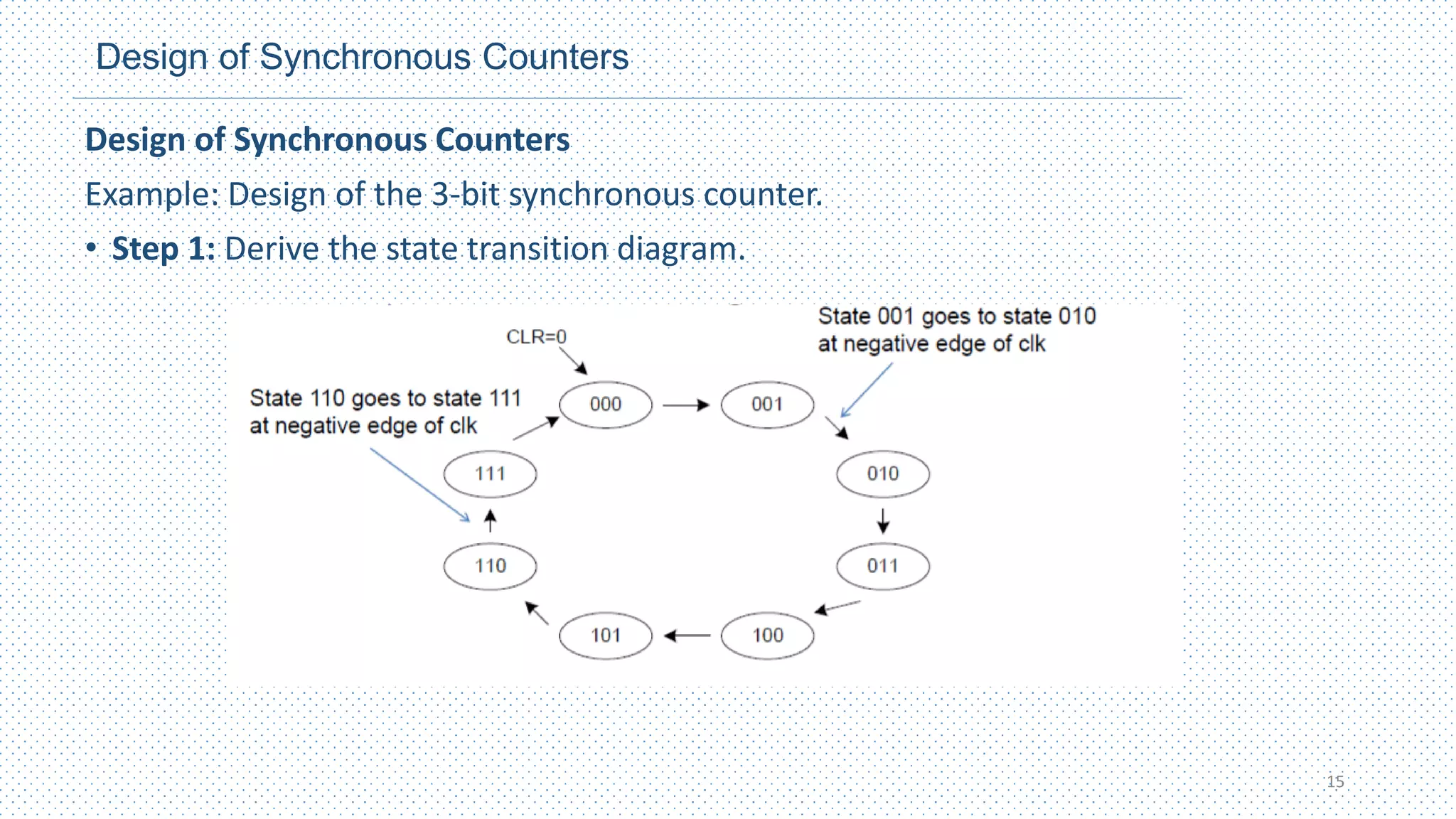
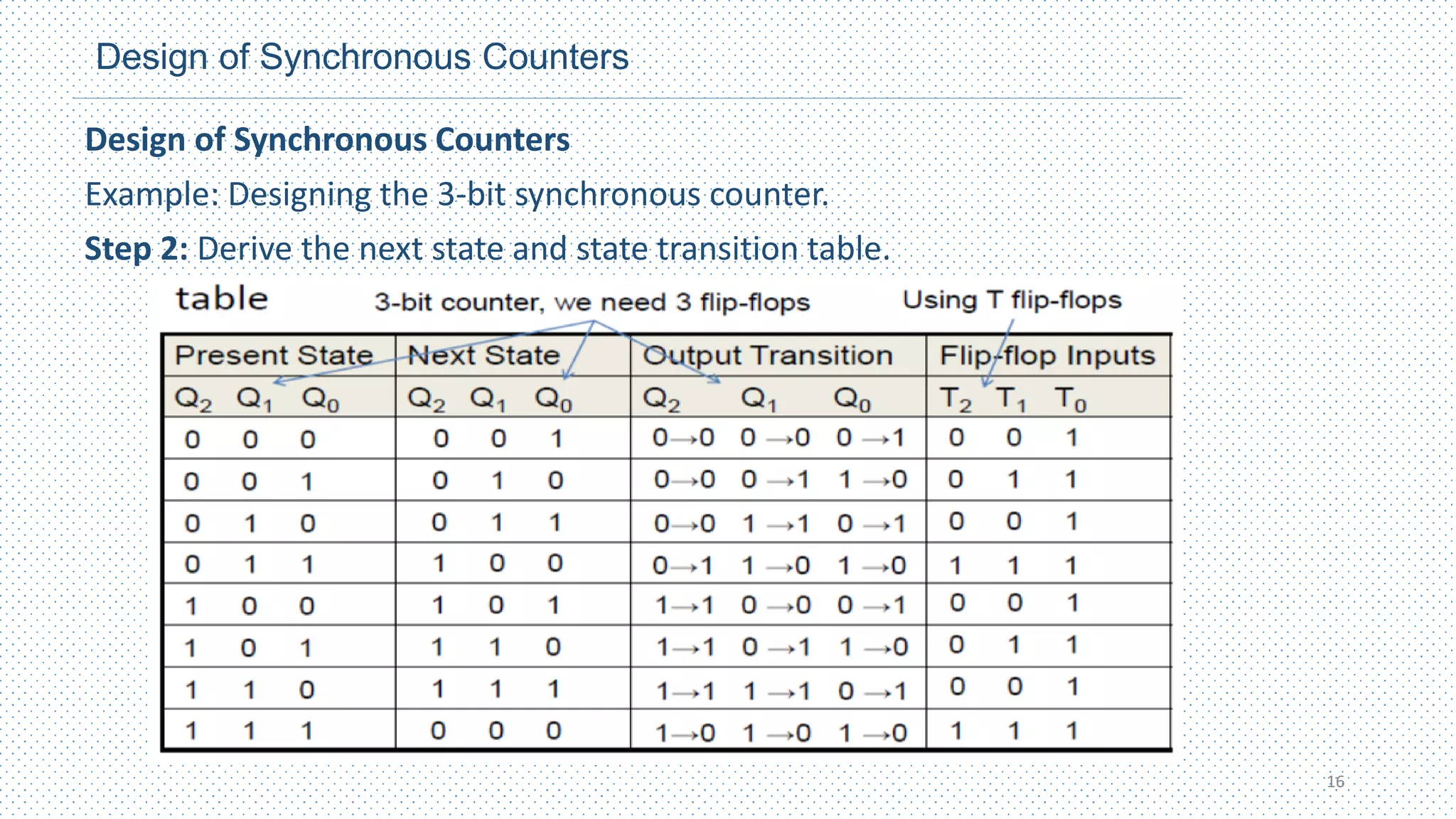
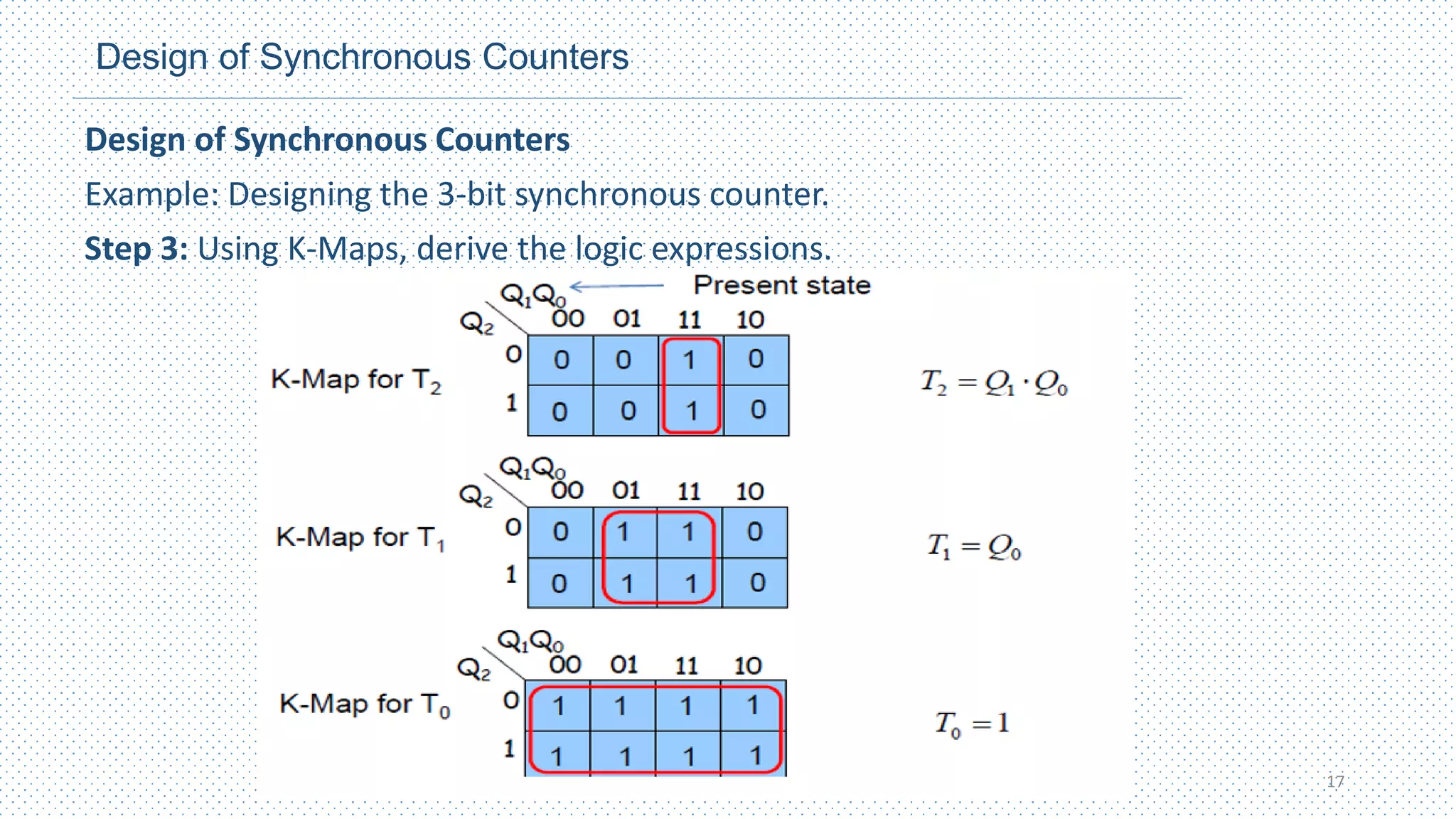
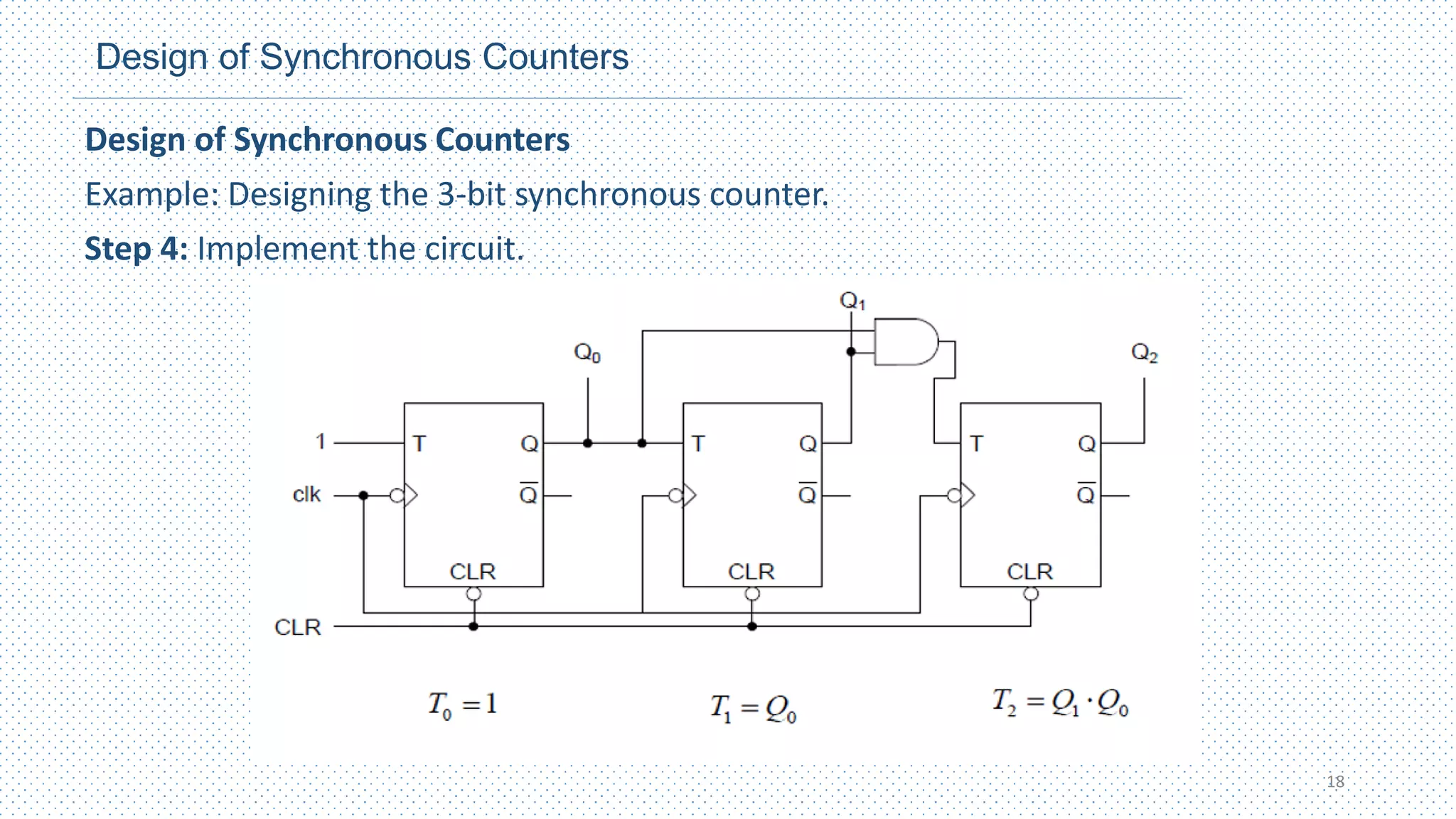
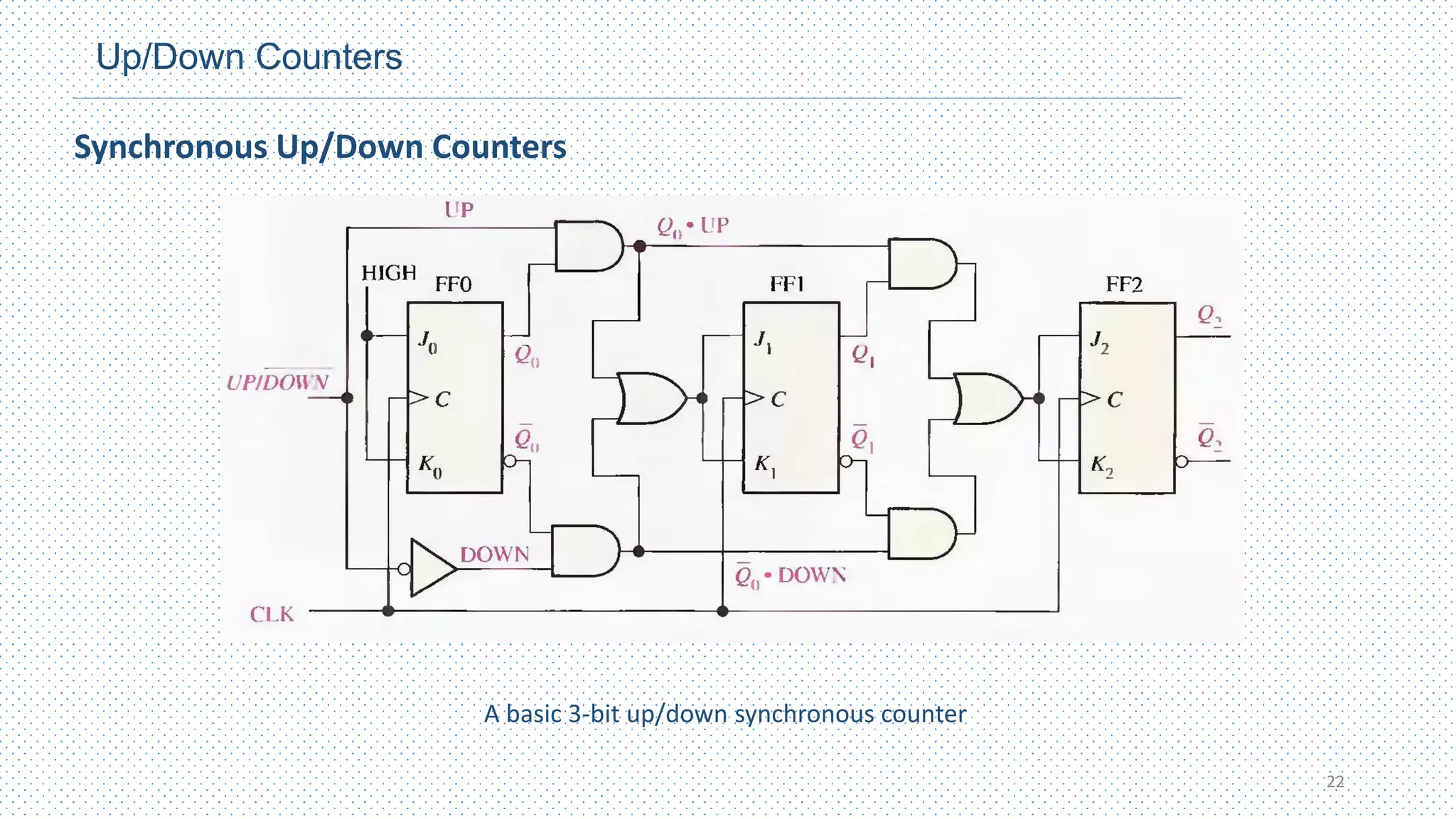
Digital Logic Design (EEEg4302) Chapter 7 : Counters This chapter discusses different types of counters, including asynchronous (ripple) counters and synchronous counters. Asynchronous counters use a ripple effect where one flip-flop triggers the next. Synchronous counters use a common clock signal to trigger all flip-flops simultaneously. The chapter also covers up/down counters, which can count up or down based on control signals, and methods for designing synchronous counters through state diagrams and logic expressions.

1. Digital Logic Design (EEEg4302)
Chapter 7 : Counters
AASTU
Department of Electrical and
Electronics Engineering
1
By Milkias H.

2. Outline
Chapter 7 : Counters
• Introduction
• Asynchronous Counters
• Synchronous Counters
• Up/Down Counters
• Design of Synchronous Counters
2

3. Introduction
• Counters – Circuits that performs the operation of counting at every clock edge.
• Counter are designed using flip-flops, Mostly the negative edge triggered.
• A counter that follows the binary number sequence is called a binary counter .
• An n ‐bit binary counter consists of n flip‐flops and can count in binary from 0
through 2n - 1.
• Counters are available in two categories: Asynchronous (ripple) counters and
synchronous counters.
• In a ripple counter, a flip‐flop output transition serves as a source for triggering
other flip‐flops. In other words, the C input of some or all flip‐flops are triggered,
not by the common clock pulses, but rather by the transition that occurs in other
flip‐flop outputs.
• In a synchronous counter, the C inputs of all flip‐flops receive the common clock.
3

4. Introduction
Benefits of counters
• Counters can act as simple clocks to keep track of “time.”
• You may need to record how many times something has happened.
• How many bits have been sent or received?
• How many steps have been performed in some computation?
• All processors contain a program counter, or PC.
• Programs consist of a list of instructions that are to be executed one after another
• The PC keeps track of the instruction currently being executed.
• The PC increments once on each clock cycle, and the next program instruction is
then executed.
4

5. Asynchronous Counters
• The term asynchronous refers to events that do not have a fixed time relationship
with each other and generally, do not occur the same time.
• Counting – Another important application of flip-flop is in digital counters. This
concept is illustrated in the following figure.
• The flip-flops are negative edge-triggered J-Ks and assume both are initially RESET.
• Flip flop A toggles on the negative going transition of each clock pulse. The Q
output of flip-flop A clocks flip-flop B. So each time QA makes a HIGH to LOW
transition, flip- flop B toggles.
• The resulting QA and QB waveforms are as shown below.(2-bit asynchronous)
5

6. Asynchronous Counters
• Exercise: Determine the output waveforms in relation to the clock for QA,QB and
QC in the circuit of the figure below. Show the binary sequence represented by
these waveforms.
3-bit Ripple(Asynchronous) counter
6

7. Asynchronous Counters
• Exercise: Determine the output waveforms in relation to the clock for QA,QB and
QC in the circuit of the figure below. Show the binary sequence represented by the
waveforms.
• Solution:
7

8. Asynchronous Counters
• The modulus of counter is the number of unique states through which the counter
will sequence.
• The maximum possible number of states(maximum Modulus) of a counter is 2𝑛
,
where n is the number of flip-flop in the counter.
• Counters can be designed to have a number of states in their sequence that is less
than the maximum of 2𝑛
. This type of sequence is called a Truncated Sequence.
• One common modulus for counters with truncated sequence is ten(MOD10).
• Counters with ten states in their sequence are called Decade counters.
• With a count sequence of zero(0000) through nine (1001) is BCD decade counters,
useful in display application in which BCD conversion is required to decimal
readout.
8

9. Asynchronous Counters
• Let’s use a 4-bit asynchronous counter and modify its sequence to illustrate the
principle of truncated counters.
• One way to make the counter recycle after the count of nine(1001) is to decode
count ten(1010) with a NAND gate and connect the output of the NAND gate to the
clear(CLR’) inputs of the flip-flops as shown below.
BCD counter
9

10. Up/Down Counters
Asynchronous Up/Down Counters
10
3- bit Asynchronous up/down counter

11. Synchronous Counters
• The term synchronous refers to events that have a fixed time relationship with
each other.
• A synchronous counter is one in which all the flip-flops in the counter are
clocked at the same time by a common clock pulse.
• The decision whether a flip‐flop is to be complemented is determined from the
values of the data inputs, such as T or J and K at the time of the clock edge.
• If T = 0 or J = K = 0, the flip‐flop does not change state. If T = 1 or J = K = 1, the
flip‐flop complements.
11

12. Synchronous Counters
A 2-bit synchronous binary counter
• Notice that an arrangement different from that for the asynchronous counter
must be used for the J1 and K1 inputs of flip- flop 1(FF1) in order to achieve a
binary sequence
• If T = 0 or J = K = 0, the flip‐flop does not change state. If T = 1 or J = K = 1, the
flip‐flop complements.
• Remember, there is a propagation delay from the triggering edge of the clock pulse
until the Q output actually makes a transition.
12

13. Synchronous Counters
A 3-bit synchronous binary counter
13

14. Design of Synchronous Counters
• There are a systematic procedure of designing synchronous counters.
Step 1: Derive the state transition diagram.
o A State Diagram shows the progression of states through which the counter advances
when it is clocked.
Step 2: Derive the next state and state transition table.
o Lists each state of counter (present state) along with the corresponding next state that the
counter goes from its present state.
Step 3: Using K-Maps, derive the logic expressions.
o K-maps can be used to determine the logic required for the inputs of the flip flop in the
counter. In this design procedure, each cell in a k-map represents one of the present
states in the counter sequence listed.
Step 4: Implement the circuit.
o The final step is to implement the combinational logic from the expressions for the inputs
and connect the flip-flops.
14

15. Design of Synchronous Counters
Design of Synchronous Counters
Example: Design of the 3-bit synchronous counter.
• Step 1: Derive the state transition diagram.
15

16. Design of Synchronous Counters
Design of Synchronous Counters
Example: Designing the 3-bit synchronous counter.
Step 2: Derive the next state and state transition table.
16

17. Design of Synchronous Counters
Design of Synchronous Counters
Example: Designing the 3-bit synchronous counter.
Step 3: Using K-Maps, derive the logic expressions.
17

18. Design of Synchronous Counters
Design of Synchronous Counters
Example: Designing the 3-bit synchronous counter.
Step 4: Implement the circuit.
18

19. Up/Down Counters
Synchronous Up/Down Counters
• An UP/DOWN(Bidirectional) counter is one that is capable of progressing in either
direction through a certain sequence.
• It can have any specified sequence of states.
• A 3- bit binary counter that advances upward through its sequence (0,1,2,3,4,5,6,7)
• And then can reversed so that it goes through the sequence in the opposite
direction(7,6,5,4,3,2,1,0) is an illustration of up/down sequential operation.
• It has an up control input and a down control input.
• When the up input is 1, the circuit counts up, since the FF inputs receive their
signals from the values of the previous normal outputs of the flip‐flops.
• When the down input is 1 and the up input is 0, the circuit counts down, since the
complemented outputs of the previous flip‐flops are applied to the FF inputs.
19

20. Up/Down Counters
Synchronous Up/Down Counters
• In general, Most up/down counters can reverse at any point in their sequence. For
instance, the 3-bit binary counter can be made to go through the following
sequence:
• For the UP sequence, Q1 changes state on the next clock pulse when Q0 = 1.
• For the down sequence, Q1 changes state on the next clock pulse when Q0 = 0.
• Thus, the J1 and k1 (T1) inputs of FF1 must equal 1 under the conditions expressed
by the following equation:
20

21. Up/Down Counters
Synchronous Up/Down Counters
• For the Up sequence, Q2 changes state on the next clock pulse when Q0=Q1=1.
• For the Down sequence, Q2 changes state on the next clock pulse when Q0=Q1=0.
• Thus, the J2 and K2 inputs of FF2 must equal 1 under the conditions expressed by
the following equation:
• Each of the conditions for the J and K inputs of each flip flop produces a toggle at
the appropriate point in the sequence.
21

22. Up/Down Counters
22
A basic 3-bit up/down synchronous counter
Synchronous Up/Down Counters

23. Last slide
23