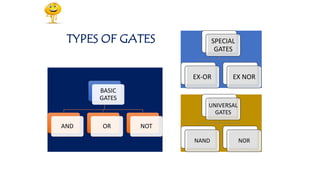
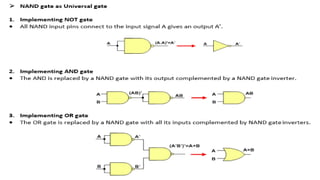
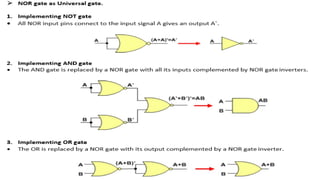
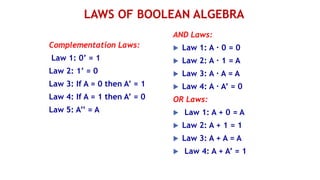
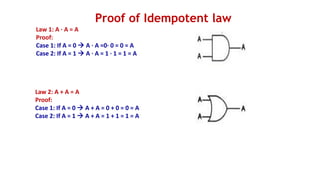
The document outlines the syllabus and course objectives for the Digital Electronics course at R.M.K. College of Engineering & Technology, focusing on digital fundamentals, combinational and sequential circuit design, semiconductor memory, and logic gate technology. It includes topics on various number systems, circuit design principles, and practical applications of digital systems. The course aims to equip students with skills to interpret digital fundamentals and construct combinational and sequential digital circuits, as well as compare different logic families.

1. R.M.K COLLEGE OF ENGINEERING & TECHNOLOGY
DEPARTMENT OF
ELECTRONICS AND COMMUNICATION ENGINEERING
EC8392- DIGITAL ELECTRONICS
By
S.Sesha Vidhya /ASP/ECE

2. SYLLABUS DISCUSSION

3. Course Objectives
1.To present the Digital fundamentals, Boolean algebra and its
applications in digital systems
2.To familiarize with the design of various combinational digital circuits
using logic gates
3.To introduce the analysis and design procedures for synchronous and
asynchronous sequential circuits
4. To explain the various semiconductor memories and related
technology
5. To introduce the electronic circuits involved in the making of logic
gates

4. UNIT I
Course Objective
1.To present the Digital fundamentals, Boolean algebra and its
applications in digital systems
DIGITAL FUNDAMENTALS
Number Systems – Decimal, Binary, Octal, Hexadecimal, 1’s and 2’s
complements, Codes – Binary, BCD, Excess 3, Gray, Alphanumeric codes,
Boolean theorems, Logic gates, Universal gates, Sum of products and product
of sums, Minterms and Maxterms, Karnaugh map Minimization and Quine-
McCluskey method of minimization.

5. UNIT II
2.To familiarize with the design of various combinational digital
circuits using logic gates
COMBINATIONAL CIRCUIT DESIGN
Design of Half and Full Adders, Half and Full Subtractors, Binary Parallel
Adder – Carry look ahead Adder, BCD Adder, Multiplexer, Demultiplexer,
Magnitude Comparator, Decoder, Encoder, Priority Encoder.

6. UNIT III
3.To introduce the analysis and design procedures for synchronous and
asynchronous sequential circuits
SYNCHRONOUS SEQUENTIAL CIRCUITS
Flip flops – SR, JK, T, D, Master/Slave FF – operation and excitation tables,
Triggering of FF, Analysis and design of clocked sequential circuits –
Design – Moore/Mealy models, state minimization, state assignment, circuit
implementation – Design of Counters- Ripple Counters, Ring Counters,
Shift registers, Universal Shift Register.

7. UNIT IV
4. To explain the various semiconductor memories and related
technology
ASYNCHRONOUS SEQUENTIAL CIRCUITS
Stable and Unstable states, output specifications, cycles and races, state
reduction, race free assignments, Hazards, Essential Hazards, Pulse mode
sequential circuits, Design of Hazard free circuits.

8. UNIT V
5. To introduce the electronic circuits involved in the making of logic
gates
MEMORY DEVICES AND DIGITAL INTEGRATED CIRCUITS
Basic memory structure – ROM -PROM – EPROM – EEPROM –
EAPROM, RAM – Static and dynamic RAM – Programmable Logic
Devices – Programmable Logic Array (PLA) – Programmable Array Logic
(PAL) – Field Programmable Gate Arrays (FPGA) – Implementation of
combinational logic circuits using PLA, PAL.
Digital integrated circuits: Logic levels, propagation delay, power
dissipation, fan-out and fan-in, noise margin, logic families and their
characteristics-RTL, TTL, ECL, CMOS

9. TEXT BOOK:
1. M. Morris Mano and Michael D. Ciletti, “Digital Design”, 5th Edition,
Pearson, 2014.
REFERENCES:
1. Charles H.Roth. “Fundamentals of Logic Design”, 6th Edition, Thomson
Learning, 2013.
2. Thomas L. Floyd, “Digital Fundamentals”, 10th Edition, Pearson
Education Inc, 2011

10. REFERENCES:
3. S.Salivahanan and S.Arivazhagan “Digital Electronics”, 1st
Edition, Vikas Publishing House pvt Ltd, 2012.
4. Anil K.Maini “Digital Electronics”, Wiley, 2014.
5. A.Anand Kumar “Fundamentals of Digital Circuits”, 4th Edition,
PHI Learning Private Limited, 2016.
6. Soumitra Kumar Mandal “ Digital Electronics”, McGraw Hill
Education Private Limited, 2016.

11. Course Outcomes(COs)
After successful completion of the course, the you should be able to
CO1:Interpret the Digital fundamentals, Boolean algebra and its
applications in digital systems.
CO2:Construct Combinational digital circuits for a given functions using
logic gates.
CO3:Implement synchronous sequential circuits for a given application.
CO4:Develop Asynchronous sequential circuits for a given application.
CO5:Experiment with various types of memory devices.
CO6:Compare the various logic families and their characteristics.

12. UNIT I
DIGITAL FUNDAMENTALS
➢ Number Systems – Decimal, Binary, Octal, Hexadecimal, 1’s and 2’s
complements
➢ Codes – Binary, BCD, Excess 3, Gray, Alphanumeric codes
➢ Boolean theorems
➢ Logic gates, Universal gates
➢ Sum of products and product of sums, Minterms and Maxterms
➢ Karnaugh map Minimization
➢ Quine-McCluskey method of minimization

13. DIGITAL ELECTRONICS
It’s a field of electronics involving the study of digital
signals and the engineering of the devices that use or
produce them.
A signal is a function that represents the variation of a
physical quantity with respect to any parameter.
(Independent quantity like Time, Distance).
What is signal?

14. Signal
Analog Digital
Continuous Discrete
https://www.youtube.com/watch?v=WxJKXGugfh8
https://www.youtube.com/watch?v=VRRbkobSsmM
https://youtu.be/C-oAyXibnJU
https://www.youtube.com/watch?v=j7-acuTio4M

15. • The system which process or works on the digital signals.
• Extensively used in computation of data processing,
control systems, communications & measurements .
DIGITAL SYSTEMS
CIRCUIT
DESIGN
LOGIC
DESIGN
SYSTEM
DESIGN

16. ❖ It has replaced many tasks of Analog systems.
❖ Also digital systems are easy to design
❖ Information storage is easy.
❖ Accuracy & precision are greater.
❖ It’s more versatile.
❖ They are less affected by noise.
❖ More digital circuitry can be fabricated on IC
chips.
❖ Reliability is more.
ADVANTAGES OVER ANALOG SYSTEM

17. Many physical quantities are Analog in nature.
❖ Which are often the inputs & outputs,
continually monitored, operated and
controlled by a system.
❖ When they are processed & expressed
digitally, we are really making a digital
approximation to an inherently analog
quantity.
LIMITATIONS OF DIGITAL TECHNIQUES
The real world
is Analog.

18. APPLICATIONS
BUSINESS
TRANSACTIONS
INDUSTRIAL
APPLICATIONS
MEDICAL
TREATMENT
DIGITAL TV,
DISKS,
TELEPHONES,
CAMERAS &
COMPUTERS
WEATHER
MONITORING
TRAFFIC
CONTOL &
COMMUNICA
TION
SYSTEM

19. NUMBER SYSTEM
➢ Introduction to Number Systems
➢ Counting in Decimal and Binary
➢ Decimal to Binary Conversion
➢ Binary to Decimal Conversion
➢ Decimal to Binary Conversion
➢ Hexadecimal Numbers
➢ Octal Numbers
➢ Bits, Bytes and Word
NUMBER SYSTEM

20. Information Representation
▪Elementary storage units inside computer are electronic switches.
Each switch holds one of two states: on (1) or off (0).
▪We use a bit (binary digit), 0 or 1, to represent the state.
ON OFF
▪In general, N bits can represent 2N different values.
▪For M values, bits are needed.
1 bit - represents up to 2 values (0 or 1)
2 bits - rep. up to 4 values (00, 01, 10 or 11)
3 bits - rep. up to 8 values (000, 001, 010. …, 110, 111)
4 bits - rep. up to 16 values (0000, 0001, 0010, …, 1111)
 
M
2
log

21. Positional Notations
➢Decimal number system, symbols = { 0, 1, 2, 3, …, 9 }
➢Position is important
➢Example:(7594)10 = (7x103) + (5x102) + (9x101) + (4x100)
➢In general, (anan-1… a0)10 = (an x 10n) + (an-1 x 10n-1) + … + (a0 x
100)
➢(2.75)10 = (2 x 100) + (7 x 10-1) + (5 x 10-2)
➢In general, (anan-1… a0 . f1f2 … fm)10 = (an x 10n) + (an-1x10n-1) + …
+ (a0 x 100) + (f1 x 10-1) + (f2 x 10-2) + … + (fm x 10-m)

22. Other Number Systems
▪ Binary (base 2): weights in powers-of-2. Binary digits (bits): 0,1.
▪ Decimal(base 10): weights in powers-of-10, Decimal digits: 0, 1,
2, 3, …, 9
▪ Octal (base 8): weights in powers-of-8. Octal digits:
0,1,2,3,4,5,6,7
▪ Hexadecimal (base 16): weights in powers-of-16. Hexadecimal
digits: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F

24. BINARY NUMBERSYSTEM
DIGITS
BASE
0,1
1*21
1*20
2
1011
1*23
0*22

25. DECIMAL NUMBER SYSTEM
0,1,2,3,4,5,6,7,8,9
DIGITS
10
BASE
5*10
7245
4*10
2*10
7*10
3
0

26. OCTALNUMBERSYSTEM
DIGITS
8
BASE
0,1,2,3,4,5,6,7
7*80
6*82
4*83
4637
3*81

27. HEXADECIMAL NUMBER SYSTEM
DIGITS
BASE
• 0,1,2,3,4,5,6,7,
• 8,9,A,B,C,D,E,F
16
6*161
A*160
B*16
2
2*16
3
2B6A

29. CONVERSION AMONG BASES
Hexadecimal
Decimal Octal
Binary

30. • Groupinto 3's startingat least significant symbol
• Write one octal digit for each group
Example: Convert (10011111)2to ( )8
010 011 111
2 3 7
Answer= (237)8
BINARY TO OCTAL
ifthe number of
bits is notevenly
divisible by3, then
add0's at the most
significant end

31. Answer= (011111110)2
OCTAL TO BINARY
Example: Convert(376)8
376
011 111
110

32. BINARY TO HEXADECIMAL
• Group into 4's starting at leastsignificantsymbol write1 hex digit for
eachgroup.
E.g Convert(1010111010)2to()16
10 1011 1010
A
2 B
Answer= (2BA)16
If the number of
bits is not evenly
divisible by 4,
then add 0's at
the most
significant end.

33. HEXADECIMAL TO BINARY
• For each of the Hexa digit write its binary equivalent.
E.g: Convert(35B1)16to()2
35 B1
0011
0101 1011
0001
Answer= (0011010110110001)2
use 4 bits
to
represent

34. Steps
❖ Convertoctalnumberto itsbinary equivalent.
❖ Convertbinarynumberto itshexadecimalequivalent.
E.g.: Convert (736.35)8to ()16
7 3 6 . 3 5
000 111 011 110 . 011 101 00
1 D E . 7 4
OCTAL TO HEXADECIMAL
ANSWER: (1DE.74 )16

35. Steps
1.Convert hexadecimal numberto itsbinaryequivalent.
2.Convertbinarynumberto itsoctalequivalent
E.g.Convert (A4C.6)16 = ( )8
HEXADECIMAL TO OCTAL
A 4 C . 6
1010 0100 1100 . 0110
00
5 1 1 4 . 3 0
ANSWER: (5114.30 )8

36. ANY BASE TO DECIMAL
❖Convertingfromany base to decimal is done by multiplying
each digit byits weight and summing.
➢(1101.101)2 = 123 + 122 + 120 + 12-1 + 12-3
= 8 + 4 + 1 + 0.5 + 0.125 = (13.625)10
➢(572.6)8 = 582 + 781 + 280 + 68-1
= 320 + 56 + 2 + 0.75 = (378.75)10
➢(2A.8)16 = 2161 + 10160 + 816-1
= 32 + 10 + 0.5 = (42.5)10
➢(341.24)5 = 352 + 451 + 150 + 25-1 + 45-2
= 75 + 20 + 1 + 0.4 + 0.16 = (96.56)10

37. DECIMAL TO ANYBASE
Decimal Toany
Base
Integer Part
Successive
Division Method
Fractional Part
Successive
Multiplication
Method

38. StepsinSuccessiveDivisionMethod
1. Divide the integer part ofdecimal number bydesired base number, store
quotient(Q)and remainder(R).
2. Consider quotient asa new decimal number and repeat Step1untilquotient
becomes 0.
3. Listthe remainders in thereverse order.
Stepsin SuccessiveMultiplicationMethod
1. Multiply the fractional part of decimalnumber by desired base number.
2. Record the integer part of product as carry and fractional part as new fractional
part.
3. RepeatSteps1and 2until fractional part of product becomes 0 oruntil you have
many digits as necessaryforyour application.
4. Readcarriesdownwardstoget desired base number.

39. Convert (108)10 into binary number
(108)10 = (1101100)2
Decimal to Octal Conversion
Decimal to Binary Conversion
DECIMAL TO ANYBASE
Convert 2477.6410 into octal number
(2477.64)10 = (4655.5075)8

40. Decimal to Hexadecimal Conversion
Convert (2479)10 into Hexadecimal number
(2479)10 = (9AF)16
Groupings of Binary Digits
•Bit 1-bit (0 or 1)
•Nibble 4-bits (such as 1101)
•Byte 8-bits (such as 1100 0111)
•Word 16-bits (common definition)
•Double-word 32-bits
•Quad-word 64-bits

41. Electronic Translators
Devices that convert from decimal to binary numbers
and from binary to decimal numbers.
Encoders -
translates from decimal to binary
Decoders -
translates from binary to decimal
41

42. Electronic Encoder –
Decimal to Binary
0
Decimal
to
Binary
Encoder
Binary output
Decimal input
0 0 0 0
5
0 1 0 1
7
0 1 1 1
3
0 0 1 1
• Encoders are available in IC form.
• This encoder translates from decimal input to binary
(BCD) output.
42

43. Binary-to-
7-Segment
Decoder/
Driver
Electronic Decoding –
Binary to Decimal
Binary input
0 0 0 0
Decimal output
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
• Electronic decoders are available in IC form.
• This decoder translates from binary to decimal.
• Decimals are shown on an 7-segment LED display.
• This decoder also drives the 7-segment display.
43

44. 1’SCOMPLEMENT
The 1’s complement of a binary number is the number that
results when we change all 1’s to zeros andthezeros to ones.
1 1 0 1 0 0 1 0
NOT OPEARATION
0 0 1 0 1 1 0 1

45. 2’SCOMPLEMENT
The 2’s complementthebinarynumberthatresultswhen add 1
to the 1’s complement.It’sgiven as,
2’s complement = 1’s complement + 1
Example Express 35in8-bit 2’scomplementform.
35in8-bit form is 00100011
+
0 0 1 0 0 0 1 1
1 1 0 1 1 1 0 0
1
1 1 0 1 1 1 0 1
1’s complement

46. 1’s complement subtraction
1.Perform 1’s complement subtraction 1010 – 1410
Binary equivalent of 10 = 1010
Binary equivalent of 14 = 1110
Complement of 14 = 0001
Add 10 = 1010
1011
Since there is no carry, take 1’s complement and
prefix negative sign.
Hence the answer is -0100
2.Perform 1’s complement subtraction 1410 –
1010
Binary equivalent of 10 = 1010
Binary equivalent of 14 = 1110
Complement of 10 = 0101
Add 14 = 1110
1 0011
Since a carry is generated, add carry and write the
answer.
0011
+1
Answer 0100

48. 1’s complement subtraction

49. 1’s complement subtraction

50. Procedure for the 2’s complement Subtraction
 Step 1:Add the minuend to the 2’s complement of the
subtrahend.
 Step 2 :If sum produces carry , discard the end carry and
record the result as positive.
 Step 3 :If sum does not generate carry ,take the 2’s
complement of the sum and place a negative sign in front
of the result .

51. 2’s complement subtraction
1.Perform 2’s complement subtraction 1010 – 1410
Binary equivalent of 10 = 1010
Binary equivalent of 14 = 1110
1’s Complement of 14 = 0001
+1
2’s Complement of 14= 0010
Add 10 = 1010
1100
Since there is no carry, take 2’s complement and
prefix negative sign.
Hence the answer is -0100
2.Perform 2’s complement subtraction 1410 – 1010
Binary equivalent of 10 = 1010
Binary equivalent of 14 = 1110
1’s Complement of 10 = 0101
+1
2’s Complement of 10
Add 14
= 0110
= 1110
1 0100
Discard the carry and write the Answer
Hence, the answer is 0100.

52. 2’s complement Subtraction

53. 2’s complement subtraction

54. 9’SCOMPLEMENT
The 9’scomplementof a decimaldigitisthe number thatmust be
addedto itto produce9.The complementof 3is 6,thecomplementof
7is 2.
Example:Obtain 9’s complementof 7493
Solution:
9 9 99
- 7 4 9 3
2 5 06 9’s complement

55. 10’SCOMPLEMENT
The10’scomplementof thegivennumberis obtainedby adding1
to the9’s complement.Itisgivenas,
10’s complement = 9’s complement + 1
Example:Obtain10’scomplementof 6492
Solution:
9999 3507
- 6 49 2 + 1
3 5 07 3 5 08 10’s complement

56. BINARY ADDITION
EXAMPLE
+
1
0
1
1
0
1
0
0
1 0 0 1 0
Carry

57. BINARY SUBTRACTION
• The Subtraction Consists of Four Possible ElementaryOperations.
• InCase ofSecondOperationtheMinuend bit is Smaller than the
Subtrahend bit, hence 1is borrowed.
0-0=0
0-1=1(borrow 1)
1-0=1
1-1=0
0
- 0
1
1
0
1
1
0
1 1 1 1
1
1 Borrow
EXAMPLE
Operations

58. BINARY MULTIPLICATION & DIVISION
e.g.: Multiply110 by 10
*
1 1
1
0
0
0 0 0
+ 1 1 0
1 1 0 0
e.g.: Divide110 by 10 1 1
10 1 1 0
1 0
0 1 0
1 0
0 0

59. Logic gate
• A logic gate is a small transistor circuit, which is
implemented in different forms within an
integrated circuit. Each type of gate has one or
more (most often two) inputs and one output.
• Logic gates are the basic building blocks of any
digital system.

60. BASIC
GATES
AND OR NOT
TYPES OF GATES SPECIAL
GATES
EX-OR EX NOR
UNIVERSAL
GATES
NAND NOR

61. Truth table & Symbol
Switching Circuit
AND GATE
IC 7408
PIN DIAGRAM
Q=A.B
Pin Diagram

62. OR GATE
Truth table & Symbol Switching Circuit Pin Diagram
A HIGH output (1) results if any of the input is
HIGH .Otherwise LOW output results.
The OR gate is a basic
digital logic gate that
implements logical
disjunction (Addition).

63. NOT GATE
Truth table & Symbol Pin Diagram
Switching Circuit
A HIGH output (1)
results if the input
to the NOT gate is
LOW (0), otherwise
HIGH (1).

64. UNIVERSAL GATES
They can replace
all other basic
gates.
Number of IC’s
used will be
reduced, in turn
space, size and cost
of the circuit would
be reduced

65. NAND GATE
Truth table & Symbol Switching Circuit Pin Diagram
IC 7400
The NAND gate
implements logical
inversion of AND
gate.
It produces LOW
output (0), if all the
input is HIGH (1),
Otherwise output
is HIGH (1).

66. NOR GATE
The NOR gate is a basic digital
logic gate that implements
logical inversion of OR gate.
Truth table & Symbol Switching Circuit Pin Diagram
It produces HIGH
output (1), if all the
input is LOW (0),
Otherwise output is
LOW (0).

67. X-OR GATE
Pin Diagram
Switching Circuit
IC 7486
.
The XOR gate is a
derived logic gate that
produces HIGH logic
output, when the inputs
are different
Truth table & Symbol

68. XNOR GATE
Truth table & Symbol
Switching Circuit
Pin Diagram
It implements logical
inversion of XOR
gate that produces
HIGH logic output,
when all the inputs
are same.

71. CODES
Binary Codes:
The digital data is represented, stored and transmitted as group of bits. This group
of bits is also called as binary code.
Binary codes can be classified into two types Weighted codes
Unweighted codes
Weighted codes
In a weighted code each bit position is assigned by a weighting factor.
Example: 8421, 5421, 2421, 84-2-1
8421 code is also known as Binary Coded decimal(BCD code)
Unweighted codes
Example: Gray code, Excess 3-code
Gray code
Gray code system is a binary number system in which every successive pair
of numbers differ in only one bit.

72. Example: Convert 0101 binary to gray code.
Gray to Binary Conversion
Example: Convert gray code 1101 to binary.
Binary to Gray Code Conversion
Example: Convert 1001 binary to gray code

73. Excess-3 Code
• This code doesn’t have any weights. So, it is an un-
weighted code.
• Excess-3 code of a decimal number is obtained by
adding three 0011 to the binary equivalent of that
decimal number.
• Excess-3 Code is also known as Self-
complementing code.
Value BCD Code Excess-3 Code
0 0000 0011
1 0001 0100
2 0010 0101
3 0011 0110
4 0100 0111
5 0101 1000
6 0110 1001
7 0111 1010
8 1000 1011
9 1001 1100
Alphanumeric Codes
• Alphanumeric codes, also called character codes used to represent
alphanumeric data.
• The alphanumeric data includes letters of the alphabet, numbers,
mathematical symbols and punctuation marks

74. BOOLEAN ALGEBRA
 Inventor of Boolean algebra was George Boole (1815 - 1864).
 Designing of any digital system there are three main
objectives;
 Build a system which operates within given
specifications
 Build a reliable system
 Minimize resources
 Boolean algebra is governed by certain rules and laws.
 Boolean algebra is different from ordinary algebra & binary
number system. In ordinary algebra; A + A = 2A and AA = A2,
here A is numeric value.
 In Boolean algebra A + A = A and A.A = A, here A has logical
significance, but no numeric significance.

75. Symbolic Logic uses values, variables and operations :
− True is represented by the value 1.
− False is represented by the value 0.
Variables are represented by letters( A) and can have one of two
values, either 0 (A’)or 1(A).
Operations are functions of one or more variables.
− AND is represented by X.Y
− OR is represented by X + Y
− NOT is represented by X’
.

76. Difference between Binary, Ordinary and Boolean system
Binary no.
system
Ordinary no.
system
Boolean
algebra
1 + 1 = 10 1 + 1 = 2 1 + 1 = 1
 Boolean algebra represent logical operation only.
 Logical multiplication is same as AND operation and
logical addition is same as OR operation.
 Boolean algebra has only two values 0 & 1.

77. Axioms of Boolean Algebra
 Axioms 1: 0 · 0 = 0
 Axioms 2: 0 · 1 = 0
 Axioms 3: 1 · 0 = 0
 Axioms 4: 1 · 1 = 1
 Axioms 5: 0 + 0 = 0
 Axioms 6: 0 + 1 = 1
 Axioms 7: 1 + 0 = 1
 Axioms 8: 1 + 1 = 1
 Axioms 9: 1’ = 0
 Axioms 10: 0’ = 1
AND LAWS
OR LAWS
COMPLEMENTARY LAWS

78. LAWS OF BOOLEAN ALGEBRA
Complementation Laws:
Law 1: 0’ = 1
Law 2: 1’ = 0
Law 3: If A = 0 then A’ = 1
Law 4: If A = 1 then A’ = 0
Law 5: A’’ = A
AND Laws:
 Law 1: A · 0 = 0
 Law 2: A · 1 = A
 Law 3: A · A = A
 Law 4: A · A’ = 0
OR Laws:
 Law 1: A + 0 = A
 Law 2: A + 1 = 1
 Law 3: A + A = A
 Law 4: A + A’ = 1

79. COMMUTATIVE LAW
For addition:- This law States
that the order in which
variables are ORed makes no
difference
For Multiplication:- This
states that the order in which
the variable ANDed makes no
difference

80. Associative Law-1
For addition:- This law states that when ORing more than two variables the result is
the same regardless of the grouping of variables

81. Associative Law-2
For Multiplication:- This law states that when ANDing more than two
variables the result is the same regardless of the grouping of variables

82. Distributive Laws
Law 1: A (B + C) = AB + AC This law states that ORing two or more
variables and than ANDing the result with
single variable is equivalent to ANDing the
Single variable with each of two or more
than two variables and then ORing the
product
Law 2: A+(B.C) =(A+B) . (A+C)
This law states that ANDing two or
more variables and than ORing the
result with single variable is
equivalent to ORing the Single variable
with each of two or more than two
variables and then ANDing the sum

83. Proof of Idempotent law
Law 1: A · A = A
Proof:
Case 1: If A = 0 → A · A =0· 0 = 0 = A
Case 2: If A = 1 → A · A = 1 · 1 = 1 = A
Law 2: A + A = A
Proof:
Case 1: If A = 0 → A + A = 0 + 0 = 0 = A
Case 2: If A = 1 → A + A = 1 + 1 = 1 = A

84. Complementation Law / Negation Law/Inverse Law
Law 1: A · A’ = 0
Proof:
Case 1: If A = 0 → A’ = 1 So, A · A’ = 0 · 1 = 0
Case 2: If A = 1 → A’ = 0 So, A · A’ = 1 · 0 = 0
Law 2: A + A’ = 1
Proof:
Case 1: If A = 0 → A’ = 1 So, A + A’ = 0 + 1 = 1
Case 2: If A = 1 → A’ = 0 So, A + A’ = 1 + 0 = 1
Double Negation Law/Involution Law
This law states that double negation of a variables is equal to the
variable itself.
Law 1: A’’ = A
Proof:
Case 1: If A = 0 → A’’ = 0’’ = 1’ = 0=A
Case 2: If A = 1 → A’’ = 1’’ = 0’ =1= A
Any odd no. of inversion is equivalent to single inversion.
Any even no. of inversion is equivalent to no inversion at all.

85. Identity Law
Law 1: A · 1 = A
Proof:
Case 1: If A= 1 → A · 1 = 1 · 1 = 1 = A
Case 2: If A= 0 → A · 1 = 0 · 1 = 0 = A
Law 2: A + 1 = 1
Proof:
Case 1: If A= 1 → A + 1 = 1 + 1 = 1
Case 2: If A= 0 → A + 1 = 0 + 1 = 1
Null Law/Dominant Law
Law 1: A · 0 = 0
Proof:
Case 1: If A= 1 → A · 0 = 1 · 0 = 0 = 0
Case 2: If A= 0 → A · 0 = 0 · 0 = 0 = 0
Law 2: A + 0 = A
Proof:
Case 1: If A= 1 → A + 0 = 1 + 0 = 1 = A
Case 2: If A= 0 → A + 0 = 0 + 0 = 0 = A

86. Proof of Absorption Law
Law 1: A + AB = A
Proof: L.H.S. = A + AB
= A (1 + B)
= A (1)
= A
R.H.S.
Law 2: A (A + B) = A
Proof: L.H.S. = A (A + B)
= A · A + AB
= A + AB
= A (1 + B)
= A (1)
= A
= R.H.S.

87. Boolean theorems and Laws
Boolean theorems and laws are used to simplify the various logical expressions. In a digital
designing problem, a unique logical expression is evolved from the truth table. If this logical
expression is simplified the designing becomes easier.

88. Principle of Duality
• It states that:
• If a theorem holds good in Boolean algebra , then by
i. Interchanging 0 to 1 and vice versa
ii. Interchanging + to . and vice versa
iii. Keeping the form of variables as such also holds true.
• The result obtained by doing so is called dual of the theorem.

89. Principle of Duality

91. Demorgan’s Theorem

92. Summary of Rules and Laws of Boolean Algebra

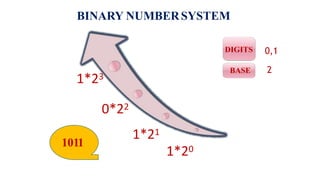
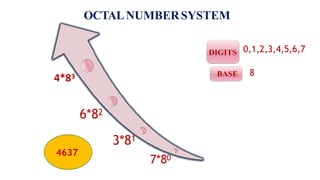
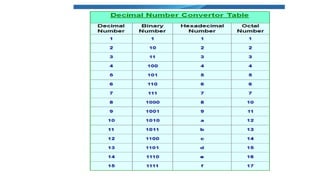
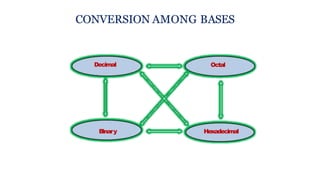
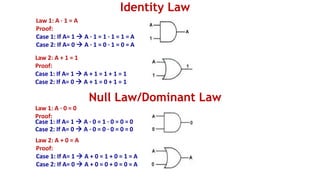
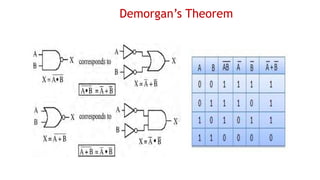
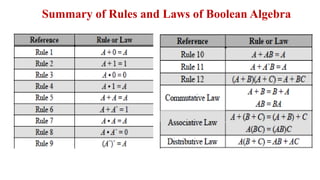
93. MINIMIZATION OF BOOLEAN EXPRESSIONS
EXAMPLE 1: [(A + B’) (C + D’)]’
= (A + B’)’ + (C + D’)’
= A’ B’’ + C’D’’
= A’B + C’D
EXAMPLE 2: REDUCE A (A + B)
=A (A + B) = AA + AB
= A (1 + B) [1 + B = 1]
= A

94. EXAMPLE 3 : [(AB)’ + A’ + AB]’
= (AB)’’ · A’’ · (AB)’
= ABA (A’ + B’)
= ABA’ + ABB’
= 0
EXAMPLE 4 : Y = (A + B) (A + C’) (B' + C’)
= (AA' + AC +A'B +BC) (B' + C') [A.A' = 0]
= (AC + A'B + BC) (B' + C’)
= AB'C + ACC' + A'BB' + A'BC' + BB'C + BCC’
= AB'C + A'BC'

95. EXAMPLE 5 : SHOW THAT (X + Y' + XY) (X + Y') (X'Y) = 0
(X + Y' + XY)(X + Y')(X'Y)
= (X + Y' + X) (X + Y’) (X' + Y) [A + A'B = A + B]
= (X + Y’) (X + Y’) (X’Y) [A + A = 1]
= (X + Y’) (X’Y) [A.A = 1]
= X.X' + Y'.X'.Y = 0 [A.A' = 0]
EXAMPLE 6 : PROVE THAT ABC + ABC' + AB'C + A'BC = AB + AC + BC
ABC + ABC' + AB'C + A'BC
=AB(C + C') + AB'C + A'BC
=AB + AB'C + A'BC =A(B + B'C) + A'BC
=A(B + C) + A'BC
=AB + AC + A'BC
=B(A + C) + AC
=AB + BC + AC

96. Minterms Vs Sum of Product (SOP)
A minterm is a product (AND) of all variables in the function, in the direct or
complemented form
Sum-of-Product (SOP) form: When two or more product terms are
summed by Boolean addition.
For n variables, there are 2n distinct minterms
Sum of Products (SOP)
X Y F Minterm Symbol
0 0 0 X’.Y’ m0
0 1 0 X’.Y m1
1 0 1 X.Y’ m2
1 1 1 X.Y m3
SOP is F(X,Y) = X.Y’ + X.Y =m2+m3
=∑m(2,3)

97. Maxterm Vs Product of Sum (POS )
A maxterm is a sum (OR) of all the variables in the function, in direct or
complemented form
Product-of-Sum (POS) form: When two or more sum terms are multiplied by
Boolean multiplication.
Product of Sum (POS)
X Y F Maxterm symbol
00 0 X+Y M0
01 1 X+Y’ M1
10 0 X’+Y M2
1 1 0 X’+Y’ M3
POS is F(X,Y) = (X+Y)(X’+Y)(X’+Y’)
= ∏M(0,2,3)=M0.M2.M3

98. Minterms and Maxterms for 3 Variables

99. A B C F
0 0 0 1
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 0
1 1 0 1
1 1 1 1
Write the SOP form of a Boolean function F, which
is represented by the following truth table
F = A’B’C’ + A’BC + ABC’ + ABC
x y z F
0 0 0 1
0 0 1 1
0 1 0 1
0 1 1 0
1 0 0 0
1 0 1 1
1 1 0 0
1 1 1 1
Write the POS form of a Boolean function F, which
is represented by the following truth table
F =(X+Y’+Z’)(X’+Y+Z)(X’+Y’+Z)
FOR PRACTICE

100. Canonical Forms
Any boolean expression can be expressed in Sum of Product (SOP) form or Product of Sum (POS) form, they are
called Canonical form.
Standard SOP - Sum of Product:
A standard SOP form is one in which a no. of product terms, each one of which contains all the variables of the
function either in complemented or non-complemented form, summed together.
➢ Each of the product term is called minterm.
➢ For minterms, Each non-complemented variable → 1 , Each complemented variable → 0
➢ Decimal equivalent is expressed in terms of lower case ‘m’.
For example,
1. XYZ = 111 = m7
2. A’BC = 011 = m3
Example 1 : F1 = X’Y’Z + XY’Z’ + XYZ
= 001 + 100 + 111
= m1 + m4 + m7
= Σm(1,4,7)
Example 2: F3 = XY’ZW + XYZ’W’ + X’Y’Z’W’
= 1011 + 1100 + 0000
= m11 + m12 + m0
= Σm(0,11,12)

101. Standard POS - Product of Sum
A Standard POS form is one in which a no. of sum terms, each one of which contains all the variables of the
function either in complemented or non-complemented form, are multiplied together.
➢ Each of the product term is called MAXTERM.
➢ For maxterms, Each non-complemented variable → 0 Each complemented variable → 1
➢ Decimal equivalent is expressed in terms of upper case ‘M’.
For example,
1. X+Y+Z = 000 = M0
2. P’+Q’+R’ = 111 = M7
Example 1: F3 = (A’+B+C)(A+B’+C)(A+B+C’)
= (100) (010) (001)
= M4 M2 M1
= ΠM(1,2,4)
Example 2: F1 = (P’+Q)(P+Q’)
= (10)(01) = M2·M1
= ΠM(1,2)

102. Canonical SoP and PoS forms
Canonical SoP form
➢ In this form, each product term contains all literals.
➢ Canonical SoP form is also called as sum of minterms form.
Canonical PoS form
➢ In this form, each sum term contains all literals.
➢ Canonical PoS form is also called as product of Maxterms form.
F(A,B,C)=ABC+AB’C(CANONICAL SOP)
F(A,B,C)=A+B’C(MINIMAL SOP)
F(A,B,C)=(A+B)(B’+C)( MINIMAL POS )
F=(A+B+C)(A’+B+C’) ( CANONICAL POS )

103. 1.Convert the given minimal SOP into standard
SOP Y = A C + B C + A B
2.Convert the given minimal POS into Standard
POS Y = (A + B) (B + C) (A + C)
F(A,B,C)=∑(111,101,011,110)
=m7, m5,m3, m6
=Σ(3,5,6,7) STANDARD SOP or
CANONICAL SOP or SUM OF MINTERMS
F(A,B,C)=Π(000,001,100,010)
=M0,M1,M4, M2
=Π(0,1,2,4) STANDARD POS or
CANONICAL POS or PRODUCT OF MAXTERM

104. Conversion Between Canonical forms
Conversion of SOP form to POS form
The SOP function F(A,B,C) = ∑(0, 2, 3, 5, 7)
 Step 1: changing the operational sign to Π
 Step 2: writing the missing indexes in the given function
Writing down the new equation in the form of POS form,
F(A,B,C) = Π(1, 4, 6)
Conversion of POS form to SOP form
The POS function F(A,B,C) = Π (2, 3, 5)
 Step 1: changing the operational sign to Σ
 Step 2: writing the missing indexes of the terms,
Writing down the new equation in the form of SOP form,
F(A,B,C) = Σ (0, 1, 4, 6, 7)

105. Karnaugh Map (K-Map)
➢ In 1953, the American physicist Maurice Karnaugh
➢ A visual way to simplify logic expressions
➢ K-Map is a graphical representation of a truth table
➢ A method to simplify Boolean algebra expressions used in switching circuits.
➢ It gives the most simplified form of the Boolean expression
➢ A Karnaugh map is a graphical method used to obtained the most simplified form of
an expression in a standard form (Sum-of-Products or Product-of-Sums).
➢ In this method, which consists of 2
n
cells for ‘n’ variables.
➢ The adjacent cells are differed only in single bit position.(gray code)
➢ Types of K-Map:
2-variable K-Map
3-variable K-Map
4-variable K-Map
5-variable K-Map

106. Constructing a 2-Variable K-Map

107. Constructing a 3-Variable K-Map

108. Constructing a 4-Variable K-Map

109. Rules for simplifying K-maps
➢ Select the respective K-map based on the number of variables present in the
Boolean function.
➢ If the Boolean function is given as sum of min terms form, then place the
ones at respective minterm cells in the K-map.
➢ Check for the possibilities of grouping maximum number of adjacent ones. It
should be powers of two. Start from highest power of two and upto least power
of two. Highest power is equal to the number of variables considered in K-map
and least power is zero.
➢ Each grouping will give either a literal or one product term. It is known
as prime implicant.
➢ The prime implicant is said to be essential prime implicant, if atleast single ‘1’
is not covered with any other groupings but only that grouping covers.

110. 1.Groups may not include any cell containing a zero in SOP
2.Groups may be horizontal or vertical, but not diagonal.

111. 3.Groups must contain 1, 2, 4, 8, or in general 2n cells.
That is if n = 1, a group will contain two 1's since 21 = 2.
If n = 2, a group will contain four 1's since 22 = 4.

112. 4.Each group should be as large as possible.

113. 5.Groups may overlap

114. 6.Groups may wrap around the table
Summary:
1.No zeros allowed.
2.No diagonals.
3.Only power of 2 number of cells in each group.
4.Groups should be as large as possible.
5.Overlapping allowed.
6.Wrap around allowed.
Overlapping and Rolling of K-Map

115. POSSIBLE GROUPING of K-MAP(PAIR)

116. POSSIBLE GROUPING of K-MAP(QUAD)

117. POSSIBLE GROUPING of K-MAP(OCLET)

118. Boolean simplification using K-Map
1. Simplify the following Boolean function using K-Map:
F(X,Y,Z) = Ʃ(2,3,4,5).
F = X’ Y + X Y’

119. 2.Simplify the following Boolean function using K-Map:
F(X,Y,Z) = Ʃ (3,4,6,7).
F = Y Z + X Z’
3.Simplify the following Boolean function using
K-Map: F = Ʃ (1,2,3,5,7)
F = C + A’ B
EX: F = m1 + m5 + m10 + m11 + m12 + m13 + m15
EX: F = A’ C + A’ B + A B’ C + B C

120. 4. Simplify the following using K-Map:
F = Ʃ(0,2,4,5,6,7,8,10,11,12,14,15)
F = D’ + A’ B + A C
5. Simplify the following Boolean function using K-
Map: F = A’ C + A’ B + A B’ C + B C Express the
function in Minterms.
F = A’ C (B + B’) + A’ B (C + C’) + A B’ C + B C (A + A’)
= A’ B C + A’ B’ C + A’ B C + A’ B C’ + A B’ C + A B C + A’ B C
= A’ B C + A’ B’ C + A’ B C’ + A B’ C + A B C
0 1 1 0 0 1 0 1 0 1 0 1 1 1 1
F = Ʃ(1,2,3,5,7)
F = C + A’ B
6.Simplify the following using K-Map:
F = m1 + m5 + m10 + m11 + m12 + m13 + m15
F = A’ C’ D + A B C’ + A C D + A B’ C

121. 7.Simplify the following POS expression using K-Map:
F = Π (0,1,4,5,6,8,9,12,13,14)
F’ = C’ + B D’
F’ is converted into F by taking complement.
F =C.(B ’ +D)

122. 8.Simplify the following POS expression using K-Map:
F = Π (0,6,7,8,12,13,14,15)
F’ = B’ C’ D’ + A B + B C
F’ is converted into F by taking complement.
F=(B+C+D)(A’+B’)(B’+C’)

123. Don’t care term in K-Map
▪ In some digital systems, certain output conditions
never occur. This is denoted by ‘X’ in the K-Map. This term is called as Don’t
care term.
▪ Don’t care terms are grouped with Minterms and Maxterms. No need to group Don’t
care terms alone.
1.Simplify the Boolean function using K-Map:
F = Ʃ(7,8,9) + d (10,11,12,13,14,15)
F = A + B C D
2. Simplify the Boolean function using K-Map:
F = Ʃ m (1,3,7,11,15) + d (0,2,5)
F = A’ B’ + C D

124. 3. Simplify the Boolean function using K-Map:
F = Ʃ m (0,2,3,6,7) + d (8,10,11,15)
F = B’ D’ + A’ C

125. 5-variable K-Map
The 5-variable K-Map consists of two 4-variable K-Maps with variables A, B, C, D and E.
Here, variable A distinguishes between the two K-Maps as shown in the diagram.
Minterms (0 – 15) belong to A = 0
Minterms (16 – 31) belong to A = 1

126. 1. Simplify the Boolean function using K-Map:
F = Ʃ m (0,2,3,4,5,6,7,11,15,16,18,19,23,27,31)
F1 = DE + B’C + B’E’ F2 = DE + B’C’E’
F= DE + A’B’C + A’B’E’ + AB’C’E

127. 2. Simplify the Boolean function using K-Map:
F = Ʃ m (0,2,4,6,9,13,21,23,25,29,31)
F1 = B’E’ + BD’E F2 = CE + BD’E
F = BD’E + A’B’E’ + A C E

128. BC
00
0
01
1
11 10
A
BC
00
0
01
1
11 10
A
BC
00
0
01
1
11 10
A
BC
00
0
01
1
11 10
A
BC
00
0
01
1
11 10
A
BC
00
0
01
1
11 10
A
1
1 1 1
1
1
1 1
1 1 1
1 1
1
1
1 1
1 1
1 1
1
FOR PRACTICE

129. CD
00
00
01
01
11
11
10
10
AB
CD
00
00
01
01
11
11
10
10
AB
CD
00
00
01
01
11
11
10
10
AB
CD
00
00
01
01
11
11
10
10
AB
CD
00
00
01
01
11
11
10
10
AB
CD
00
00
01
01
11
11
10
10
AB
1
1
1
1
1
1
1
1
1
1
1
1 1 1
1
1 1 1
1
1
1
1
1
1
1
1 1 1 1
1 1
1 1
1
1
FOR PRACTICE

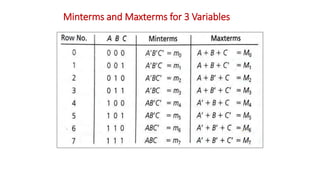
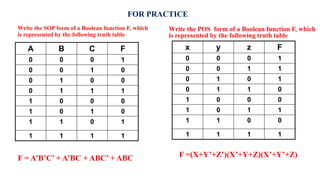
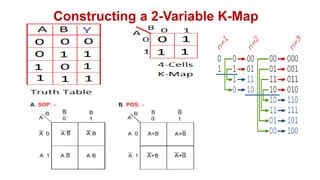
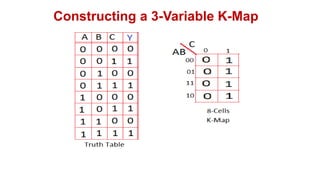
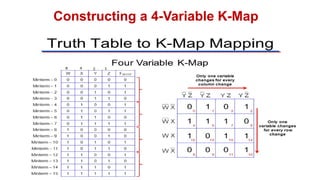
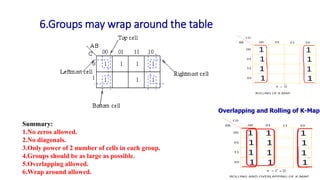
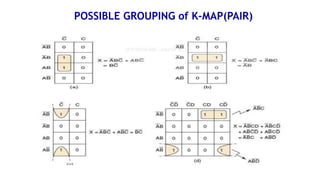
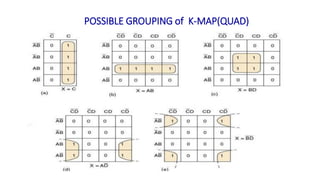
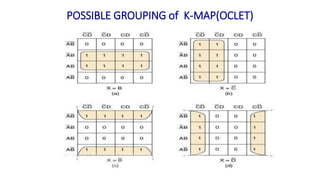
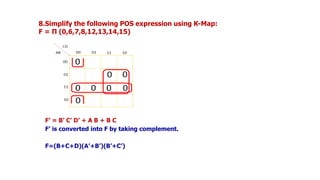
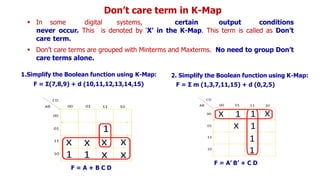
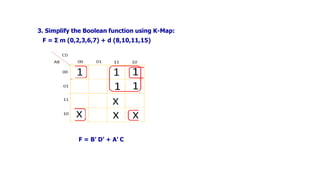
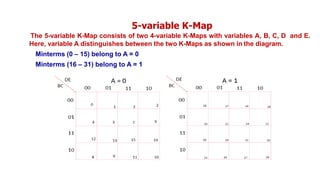
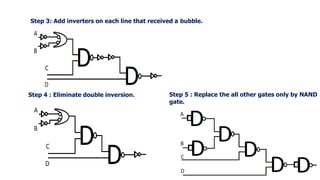
130. Realize the following Boolean Expression using NAND Gate:
F = [(A+B)C]’.D
NAND Gate Implementation
Step 1: Draw the logic diagram using basic gates.
Step 2 : Add bubbles at the output of the AND Gate and the input of the OR Gate.

131. Step 3: Add inverters on each line that received a bubble.
Step 4 : Eliminate double inversion. Step 5 : Replace the all other gates only by NAND
gate.

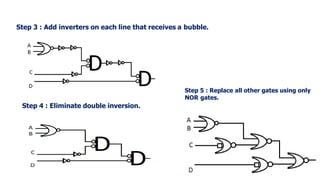
132. NOR Gate Implementation
Implement the following Boolean Expression using NOR Gate
only : F = [(A+B)C]’.D
Step 1: Draw the logic diagram using basic gates.
Step 2: Add bubbles at the output of OR gate
and input of AND gate.

133. Step 3 : Add inverters on each line that receives a bubble.
Step 4 : Eliminate double inversion.
Step 5 : Replace all other gates using only
NOR gates.

134. Tabulation Method or Quine Mc-Cluskey Method
1.Simplify the following Boolean function using Tabulation method.
F = Ʃ(0,2,3,6,7,8,10,12,13)
Step 1
Express each minterm in its binary
representation
Step 2
Arrange the minterms based on their
number of 1’s.

135. Step 3
Compare each binary number from one
group to another, if it differs only one bit
position, put a dash (-) mark and write
the remaining terms.
2-Cell combination
Step 4
Two terms can be combined only if they have
dashes in the same position and one more
differing variable is allowed.
4-Cell combination

136. Step 5
All the terms that remain unchecked during the
process are considered as prime implicants.
Prime implicants that cover minterms with a
single cross in their columns are considered
as EPI (Essential Prime Implicants)
F=B’D’+A’C+ABC’
Note: The term which are not present in the 4-cell
combination is also known as prime implicant
Verification using K-map
For the given Truth Table, the K-Map is constructed as
shown below:
F=B’D’+A’C+ABC’

137. 2.Simplify the following Boolean function using Tabulation method.
F = Ʃ(2,3,7,9,11,13) + d(1,10,15)
Step 1
Express each minterm in its binary representation
Step 2
Arrange the minterms based on their
number of 1’s

138. Step 3
Compare each binary number from one group to
another, if it differs only one bit
position, put a dash (-) mark and write the remaining
terms.
2-Cell combination
Step 4
Two terms can be combined only if they have
dashes in the same position and one more
differing variable is allowed.
4-Cell combination

139. Step 5
All the terms that remain unchecked during the process
are considered as prime implicants.
Prime implicants that cover minterms with a single
cross in their columns are considered as EPI (Essential
Prime Implicants)
Note: The term which are not present in the 4-cell
combination is also known as prime implicant.
Don’t care columns are omitted when forming prime
implicants table
F=B’C+CD+AD
Verification using K-map
F=B’C+CD+AD

140. STAY HOME…
STAY SAFE…