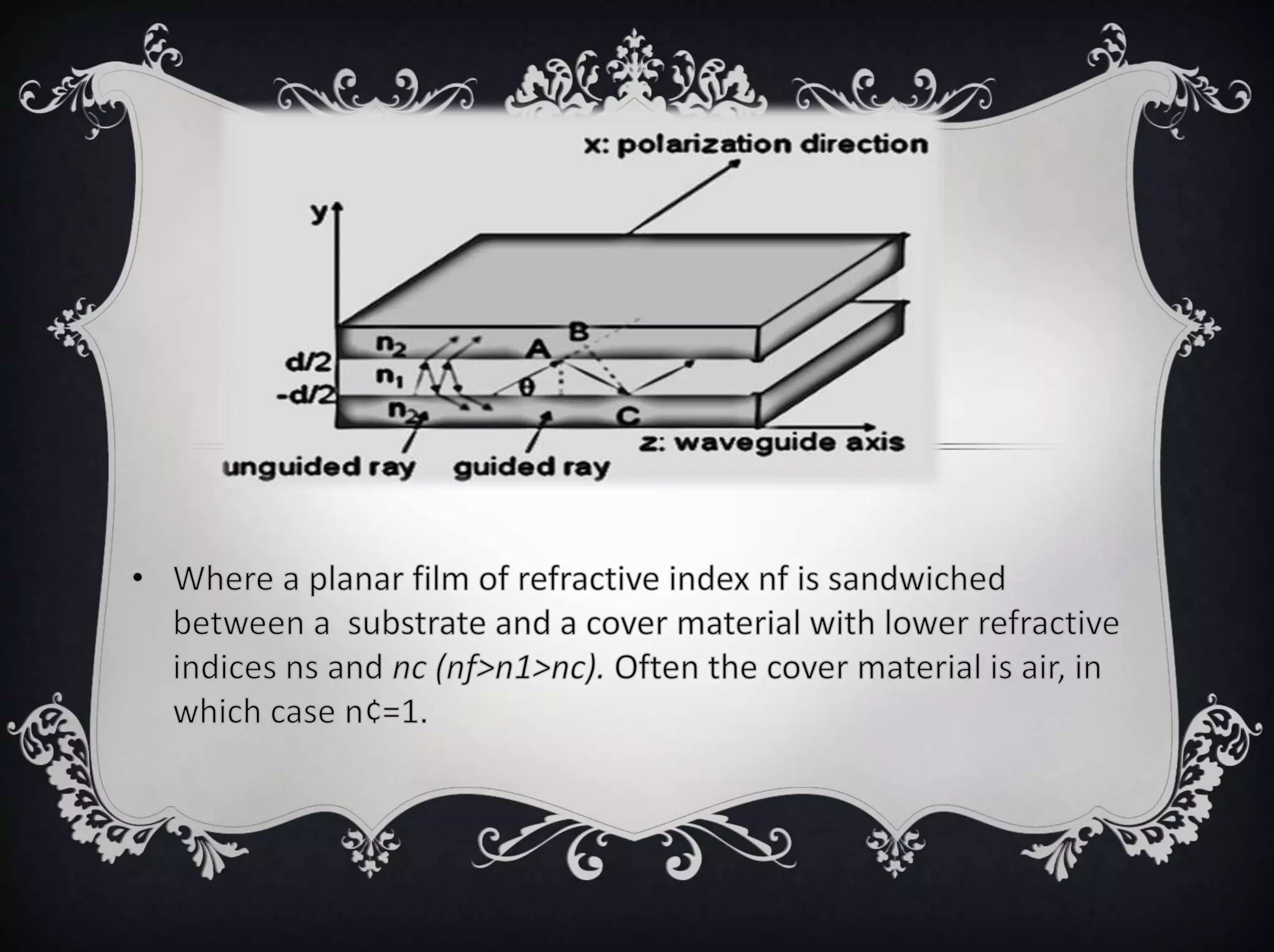
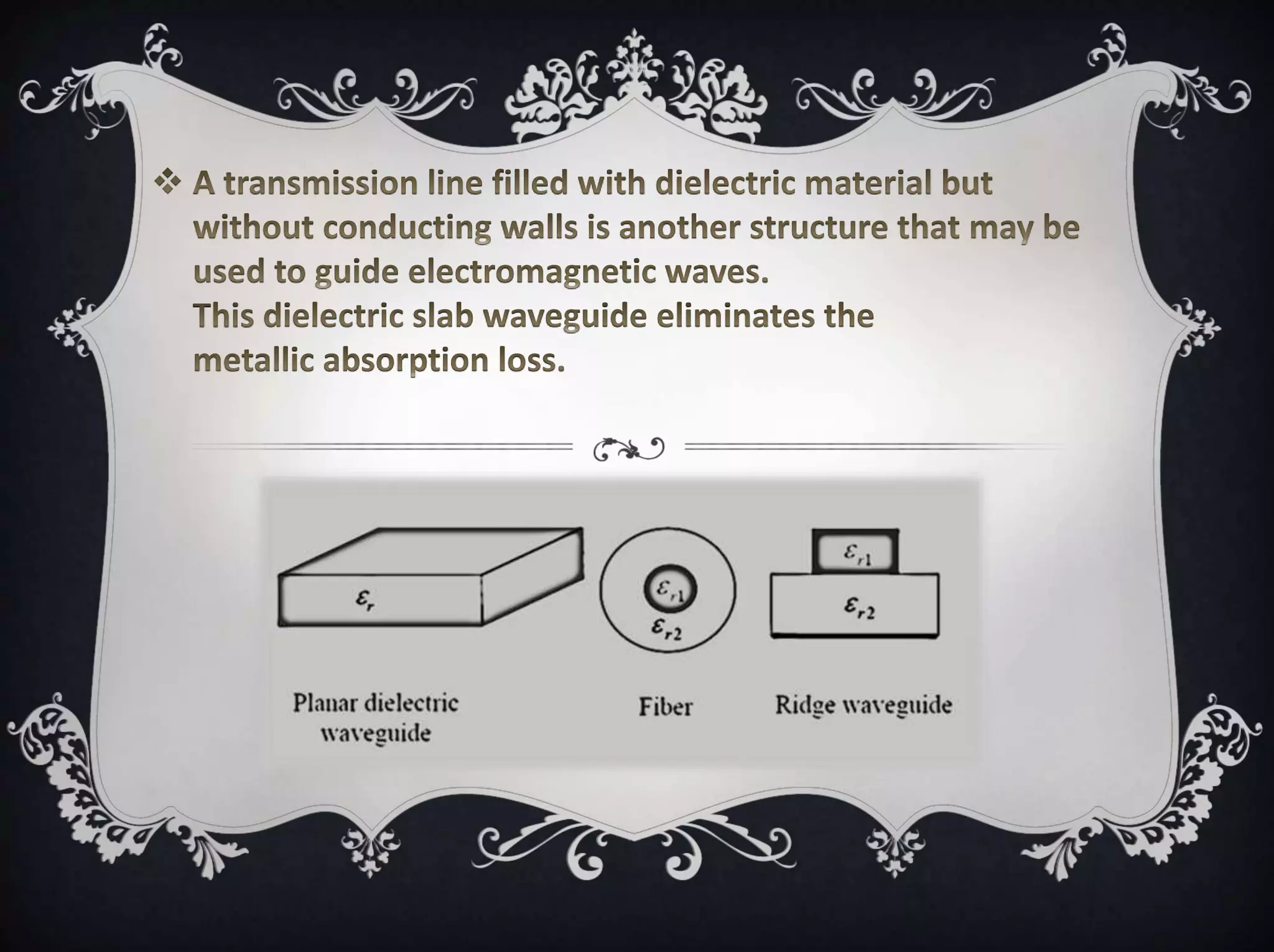
Dielectric waveguides confine and guide light using differences in the dielectric constants between core and cladding materials. They include optical fibers and planar slab waveguides. Waves propagating along dielectric waveguides can have transverse magnetic (TM) or transverse electric (TE) modes. TM and TE modes are determined by the nonzero field components and satisfy different wave equations. The solutions for the field components inside and outside the waveguide core involve sinusoidal and exponential functions that must match at boundaries to satisfy continuity. The propagation constants and decay constants of the modes relate to the waveguide structure and satisfy dispersion equations.

1. DIELECTRIC
WAVE GUIDE

2. KEY
CONCEPTS:-

3.  Dielectric waveguides are the structures
that are used to confine and guide the light
in the guided -wave devices and circuits of
integrated optics. A well -known dielectric
waveguide is, of course, the optical fiber
which usually has a circular cross -section.
In contrast, the guides of interest to
integrated optics the simplest dielectric
guide is the planar slab guide shown in fig.
INTRODUCTION: DIELECTRIC WAVE GUIDE

7. Why it is used?????

8. Consider the dielectric slab as in fig.,
Bouncing wave interpretation of propagating waves along
dielectric waveguide:

10. F o r T M w a v e s , h z = 0 , s i n c e t h e r e i s n o x - d e p e n d e n c e s o
e q . ,
w e h a v e ,
𝑑2 𝐸 𝑧
0
𝑑 𝑦2 + h2 𝐸 𝑧
0
(y) =0………..(1)
where,
h2=2+2Μ ………(2)
00
00
dd

11.  S o l u t i o n O f E q . ( 1 ) m u s t B e C o n s i d e r e d I n B o t h S l a b
A n d F r e e S p a c e R e g i o n W h i c h M a t c h A t B o u n d a r i e s .
I n S l a b R e g i o n We A s s u m e T h a t Wa v e P r o p a g a t e I n + Z
D i r e c t i o n Wi t h o u t A t t e n u a t i o n S o ,
=jβ … … . ( 3 )

12.  S o l u t i o n o f e q . I n d i e l e c t r i c s l a b ma y c o n t a i n b o t h
s i n e & c o s i n e t e r m, w h i c h a r e a n o d d & e v e n
f u n c t i o n , r e s p e c t i v e l y o f y :
𝐸 𝑧
0
( y ) = 𝐸0 s i n 𝑘 𝑦 y + = 𝐸 𝑒 C O S 𝑘 𝑦 y , | y | ≤
𝑑
2
… … ( 4 )
w h e r e ,
… … … ( 5 )
I n f r e e s p a c e r e g i o n ( y >
𝑑
2
& y <
𝑑
2
) w a v e mu s t d e c a y
e x p o n e n t i a l l y s o t h e y g u i d e d a l o n g s l a b & d o n o t
r a d i a t e a w a y f r o m i t . T h e n w e h a v e ,
𝐸 𝑧
0
( y ) =
𝑐 𝑢 𝑒
− 𝛼 𝑦 −
𝑑
2 ,
𝑐 𝑙 𝑒 𝛼 ( 𝑦 +
𝑑
2
)
,
y ≥
𝑑
2
y ≤ −
𝑑
2
… … … . ( 6 )

13. w h e r e ,
… … … . ( 7 )
e q . ( 7 ) & ( 5 ) a r e d i s p e r s i o n r e l a t i o n s b e c a u s e i t s h ow s
n o n l i n e a r d e p e n d e n c e o f p h a s e c o n s t a n t & .
Fo r f o l l ow i n g a m p l i t u d e s, we w i l l c o n s i d e r o d d &
e ve n t e r m f o r T M m o d e s.
[ A ] O d d T M m o d e :
I n T h i s M o d e 𝐸 𝑧
0
( y ) D e s c r i b e Wi t h S i n e F u n c t i o n
T h a t I s A n t i - S y mme t r i c w i t h R e s p e c t Y = 0 p l a n e .

14. i) in the dielectric region,|y|≤
𝑑
2
:
From eq.(4), and 𝐻 𝑥
0
=
𝑗 𝜔 𝜖
ℎ 2 then,
𝐸 𝑧
0
(y) = 𝐸0 sin 𝑘 𝑦 y ……(8)
𝐸 𝑦
0
(y) =(-
𝑗 𝛽
𝑘 𝑦
) 𝐸0 cos 𝑘 𝑦 y ………..(9)
𝐻 𝑥
0
(y)= =
𝑗 𝜔 𝜖 𝑑
𝑘 𝑦
) 𝐸0 cos 𝑘 𝑦 y ………(10)

15. i i ) I n u p p e r f r e e - s p a c e r e g i o n , y ≥
𝑑
2
:
𝐸 𝑧
0
(y) =( 𝐸0 sin
𝑘 𝑦 𝑑
2
) 𝑒 − 𝛼( 𝑦−
𝑑
2
)
… … … ( 1 1 )
𝐸 𝑦
0
( y ) = −
𝑗 𝛽
α
( 𝐸0 s i n
𝑘 𝑦 𝑑
2
) 𝑒 − 𝛼 ( 𝑦 −
𝑑
2
)
… … … . ( 1 2 )
𝐻 𝑥
0
(y) =−
𝑗 𝜔 𝜖0
α
( 𝐸0 sin
𝑘 𝑦 𝑑
2
) 𝑒 − 𝛼( 𝑦−
𝑑
2
)
… … ( 1 3 )
w h e r e 𝑐 𝑢 i n e q . 6 h a s b e e n s e t t o e q u a l 𝐸0 s i n
𝑘 𝑦 𝑑
2
w h i c h i s v a l u e o f e q . ( 8 ) .

16. i i ) I n l owe r s p a c e r e g i o n , y ≤ −
𝑑
2
:
𝐸 𝑧
0
(y) =−( 𝐸0 sin
𝑘 𝑦 𝑑
2
) 𝑒 𝛼 ( 𝑦 +
𝑑
2
)
… … … ( 1 4 )
𝐸 𝑦
0
( y ) = −
𝑗 𝛽
α
( 𝐸0 s i n
𝑘 𝑦 𝑑
2
) 𝑒 𝛼 ( 𝑦 +
𝑑
2
)
… … … . ( 1 5 )
𝐻 𝑥
0
(y) = 𝑗 𝜔 𝜖0
α
( 𝐸0 sin
𝑘 𝑦 𝑑
2
) 𝑒 𝛼 ( 𝑦+
𝑑
2
)
… … ( 1 6 )
w h e r e 𝑐 𝑙 i n e q . 6 h a s b e e n s e t t o e q u a l − 𝐸0 s i n
𝑘 𝑦 𝑑
2
w h i c h i s v a l u e o f e q . ( 8 ) a t l o w e r i n t e r f e r e n c e y = −
𝑑
2
.

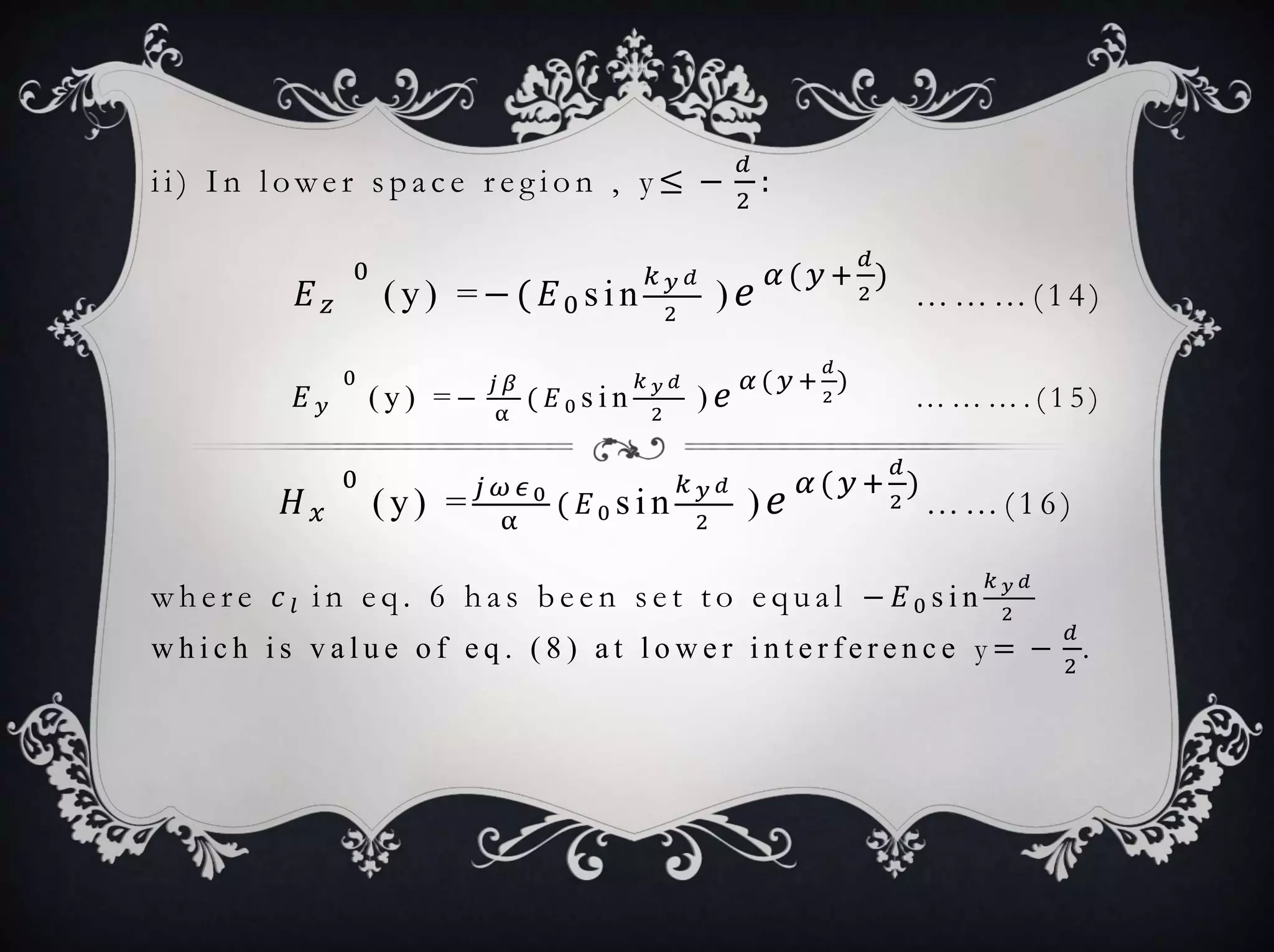
17. we must determine 𝑘 𝑦 & for given freq.,so from
eq.(10) &(13),taking ratio of them,
[ODD TM MODE]

18.  I n T h i s M o d e 𝐸 𝑧
0
( y ) D e s c r i b e W i t h C o s i n e
F u n c t i o n T h at I s A nt i - Sy m m e t r i c W i t h Re s p e c t
Y = 0 P l a n e .
𝐸 𝑧
0
( y ) = 𝐸 𝑒 C O S 𝑘 𝑦 y, | y | ≤
𝑑
2
… … . . ( 1 7 )
a n d s i m i l a r l y a s p e r e a r l i e r d i s c u s s i o n re l at i o n
o f 𝑘 𝑦 &  b e co m e s ,
[Even TM MODE]
[B] Even TM mode:

19. For TE waves, Ez = 0, since there is no x -
dependence so eq.,
𝑑2 𝐻 𝑧
0
𝑑 𝑦2 + h2 𝐻 𝑧
0
(y) =0 ……..(18)
where h2=2+2Μ ………(19)
solution of eq. 18 gives as,
𝐻 𝑦
0
(y) = 𝐻0 sin 𝑘 𝑦 y + = 𝐻 𝑒 COS 𝑘 𝑦 y, |y|≤
𝑑
2
…(20)

20. In free space region (y>
𝑑
2
& y <
𝑑
2
)wave must
decay exponentially so they guided along slab
& do not radiate away from it.Then we have,
𝐸 𝑧
0
(y) =
𝑐 𝑢 𝑒
− 𝛼 𝑦 −
𝑑
2 ,
𝑐 𝑙 𝑒 𝛼 ( 𝑦 +
𝑑
2
)
,
y≥
𝑑
2
y≤−
𝑑
2
………(21)

21. [A]odd TE Mode:
(i)In the dielectric region,|y|≤
𝑑
2
:
𝐻 𝑧
0
(y) = 𝐻0 sin 𝑘 𝑦 y …(22)
𝐻 𝑦
0
(y) =(-
𝑗 𝛽
𝑘 𝑦
) 𝐻0 cos 𝑘 𝑦 y …..(23)
𝐸 𝑥
0
(y)= =(-
𝑗 𝜔 𝜇 𝑑
𝑘 𝑦
) 𝐻0 cos 𝑘 𝑦 y …(24)

22. ii) In upper free-space region , y≥
𝑑
2
:
𝐻 𝑧
0
(y) =( 𝐻0 sin
𝑘 𝑦 𝑑
2
) 𝑒 −𝛼(𝑦−
𝑑
2
)
………(25)
𝐻 𝑦
0
(y) =−
𝑗 𝛽
α
( 𝐻0 sin
𝑘 𝑦 𝑑
2
) 𝑒 − 𝛼( 𝑦−
𝑑
2
)
……….(26)
𝐸 𝑥
0
(y) −
𝑗 𝜔 𝜇0
α
( 𝐻0 sin
𝑘 𝑦 𝑑
2
) 𝑒 −𝛼(𝑦−
𝑑
2
)
……(27)

23. ii) In lower space region , y≤ −
𝑑
2
:
𝐻 𝑧
0
(y) =−( 𝐻0 sin
𝑘 𝑦 𝑑
2
) 𝑒 𝛼( 𝑦+
𝑑
2
)
… … … ( 1 4 )
𝐻 𝑦
0
( y ) = −
𝑗 𝛽
α
( 𝐻0 s i n
𝑘 𝑦 𝑑
2
) 𝑒 𝛼 ( 𝑦 +
𝑑
2
)
… … … . ( 1 5 )
𝐸 𝑥
0
(y) =-
𝑗 𝜔 𝜇 𝑑
α
( 𝐻0 sin
𝑘 𝑦 𝑑
2
) 𝑒 𝛼( 𝑦+
𝑑
2
)
… … ( 1 6 )

24. RELATION BETWEEN of 𝑘 𝑦 & becomes,
from eq. (24) & (27)taking ratio of them
thus,
[ODD TE MODE]

25. In This Mode 𝐻 𝑧
0
(y) Describe With Cosine
Function That Is Anti - Symmetric With Respect
Y=0 Plane.
𝐻 𝑧
0
(y) = 𝐻 𝑒 COS 𝑘 𝑦 y, |y| ≤
𝑑
2
……..(28)
and similarly as per earlier discussion relation
of 𝑘 𝑦 & becomes,
[Even TE MODE]
[B] Even TE Mode:

26.  In Dielectric Waveguide ,Generally It Leads To Bessel's
Differential Eq.,Because Study Is Complicated By The Fact
Pure TM Or TE Modes Are Possible Only If The Fields Are
Circularly Symmetrical Which Means Fields AreIndependent
Of Angle Φ.
But When Fields Are Dependent On Φ, Separation Into TM
And TE Modes Is No Longer Possible,& It Is Necessary The
Existence Of Both 𝐸𝑧&𝐻𝑧 Simultaneously Which Is Known As
Hybrid Mode.
HE mode:

27. Consider an example tm mode for
rounddielectric rod of radius a and per mittivity
𝜖 𝑑 in air. From eq. 𝐸 𝑧
0
(y) = 𝑐 𝑛 𝐽 𝑛 ℎ 𝑟 𝑐 𝑜 𝑠 nΦ By
setting n=0,
where, ….(29)

28. The corresponding is ,from eq.
It gives,
𝐻∅ 𝑖
0
= -
𝑗 𝜔 𝜖 𝑑
ℎ
𝑐0 𝐽0 (hr) ……………(30)
Outside the dielectric rod ,the fields are required
to be evanescent and must decrease exponentially
with distance. An appropriate choice of 𝐸 𝑧0 &
𝐾 𝑜 (ζr) Bessel fun. Gives ,
𝐸 𝑧0
0
= 𝐷0 𝐾0 (ζr) …………(31)

29. Where, ζ
2
= 2-2Μ0 0 …..(32)
and 𝐷0 𝑖 𝑠 𝑐 𝑜 𝑛 𝑠 𝑡 𝑎 𝑛 𝑡 𝑐 𝑜 𝑟 𝑟 𝑒 𝑠 𝑝 𝑜 𝑛 𝑑 𝑖 𝑛 𝑔 𝐻∅0
0
𝑖 𝑠
𝐻∅0
0
=
𝑗 𝜔 𝜖0
ζ 𝐷0 𝐾′ 𝑜 (ζr), r≥ 𝑎 ………(33)
and the field component 𝐸 𝑧 0 & 𝐻∅
0
must be
continuous at r=a which requires,

30. FROM EQ. (29)&(31) COMBINING BOTH OF THEM
WE HAVE
𝐶0 𝐽 𝑜 (ha), = 𝐷0 𝐾 𝑜 (ζa) …..(34)
and from eq.(30) & (33)
we get by combining both of them as,
𝜖 𝑑
ℎ
𝑐0 𝐽′0 (ha)=-
𝜖0
ζ 𝐷0 𝐾′ 𝑜 (ζr), ..(35)

31. Combination of above eq. (34) & (35) for
circularly symmetrical TM modes :
where ζ and h are related through eq.(29)
And (32)
h 𝟐
+ ζ 𝟐
= 2Μ 𝟎 ( )

32. Above eq. Can be solved if the
eigenvalues found ,the cutoff
frequency's and other properties
can be determined.