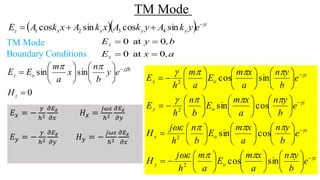
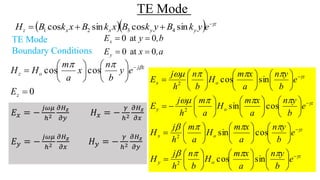
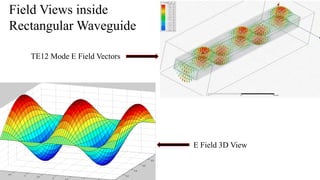
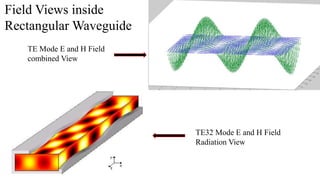
The document discusses rectangular waveguides, including their modes of propagation, fields inside, cutoff frequency, and propagation constant. It explains the transverse electric (TE) and transverse magnetic (TM) modes, showing the electric and magnetic field configurations and equations for each. Examples of electric and magnetic field views are also shown for different TE modes inside the rectangular waveguide.

1. Branch - Electronics Engineering & Related Branches
Microwave Engineering
UNIT – 2
Waveguide: Rectangular Waveguide and their Applications, Modes,
Propagation constant and Cut-off Frequency
Presented By
Avishisht Kumar

2. Learning outcomes
• What are Waveguides and its types?
• Rectangular Waveguides: Fields Inside
• Modes of Propagation
• Transverse Magnetic Mode (TM-Mode). E = (Ex; Ey; Ez) and H = (Hx; Hy; 0).
• Transverse Electric Mode (TE-Mode). E = (Ex; Ey; 0) and H = (Hx; Hy; Hz).
• Cut-off frequency and Propagation Constant
• Field Views inside Rectangular Waveguide

3. • A waveguide is a structure that guides waves, such as electromagnetic
waves or sound, with minimal loss of energy by restricting the
transmission of energy to one direction.
• A hollow metallic tube of the uniform cross section for transmitting
electromagnetic waves by successive reflections from the inner walls
of the tube is called as a Waveguide
• There are five types of waveguides are:
What are Waveguides and its types?
1. Rectangular waveguide
2. Circular waveguide
3. Elliptical waveguide
4. Single ridged waveguide
5. Double ridged waveguide

4. Rectangular Waveguides:
Fields inside
Using phasors & assuming waveguide
filled with
• lossless dielectric material and
• walls of perfect conductor,
the wave inside should obey…
∇2
𝐸 + 𝑘2
𝐸 = 0
∇2 𝐻 + 𝑘2 𝐻 = 0
where 𝑘2
= 𝜔2 𝜇𝜀 𝑐
Then applying on the z-component…
𝜕2
𝐸𝑧
𝜕𝑥2
+
𝜕2
𝐸𝑧
𝜕𝑦2
+
𝜕2
𝐸𝑧
𝜕𝑧2
+ 𝑘2 𝐸𝑧 = 0
Solving by method of Separation of
Variables:
𝐸𝑧(𝑥, 𝑦, 𝑧) = 𝑋(𝑥)𝑌(𝑦)𝑍(𝑧)
from where we obtain:
𝑋′′
𝑋
+
𝑌′′
𝑌
+
𝑍′′
𝑍
= −𝑘2
𝛻2
𝐸𝑧 + 𝑘2
𝐸𝑧
= 0

5. 𝑋(𝑥) = 𝑐1 cos 𝑘 𝑥 𝑥 + 𝑐2 sin 𝑘 𝑥 𝑥
𝑌(𝑦) = 𝑐3 cos 𝑘 𝑦 𝑦 + 𝑐4 sin 𝑘 𝑦 𝑦
𝑍(𝑧) = 𝑐5 𝑒 𝛾𝑧
+ 𝑐6 𝑒−𝛾𝑧
ℎ2 = 𝛾2 + 𝑘2 = 𝑘 𝑥
2 + 𝑘 𝑦
2
Rectangular Waveguides: Fields inside
𝑋′′
𝑋
+
𝑌′′
𝑌
+
𝑍′′
𝑍
= −𝑘2
−𝑘 𝑥
2 − 𝑘 𝑦
2 + 𝛾2
= −𝑘2
which results in the expressions:
𝑋′′ + 𝑘 𝑥
2 𝑋 = 0
𝑌′′ + 𝑘 𝑦
2 𝑌 = 0
𝑍′′
− 𝛾2
𝑍 = 0
   
  
   z
yyxxz
z
yyxxz
zz
yyxxz
eykBykBxkBxkBH
eykAykAxkAxkAE
z
ececykcykcxkcxkcE










sincossincos
,fieldmagneticfor theSimilarly
sincossincos
:direction-intravelingwaveat thelookingonlyIf
sincossincos
4321
4321
654321

6. From the previous slide equations we can conclude:
TEM (Ez=Hz=0) can’t propagate.
TE (Ez=0) transverse electric
In TE mode, the electric lines of flux are perpendicular to the axis of the
waveguide
TM (Hz=0) transverse magnetic, Ez exists
In TM mode, the magnetic lines of flux are perpendicular to the axis of the
waveguide.
HE hybrid modes in which all components exists
Modes of Propagation

7.    z
yyxxz eykAykAxkAxkAE 
 sincossincos 4321
,axE
,byE
z
z
0at0
0at0

TM Mode
Boundary Conditions
z
oy
z
ox
z
oy
z
ox
e
b
yn
a
xm
E
a
m
h
j
H
e
b
yn
a
xm
E
b
n
h
j
H
e
b
yn
a
xm
E
b
n
h
E
e
b
yn
a
xm
E
a
m
h
E
























































































sincos
cossin
cossin
sincos
2
2
2
2
0
sinsin













 
z
zj
oz
H
ey
b
n
x
a
m
EE 
𝐸 𝑥 = −
𝛾
ℎ2
𝜕𝐸 𝑧
𝜕𝑥
𝐻 𝑥 =
𝑗𝜔𝜀
ℎ2
𝜕𝐸 𝑧
𝜕𝑦
𝐸 𝑦 = −
𝛾
ℎ2
𝜕𝐸 𝑧
𝜕𝑦
𝐻 𝑦 = −
𝑗𝜔𝜀
ℎ2
𝜕𝐸 𝑧
𝜕𝑥
TM Mode

8. ,axE
,byE
y
x
0at0
0at0


   z
yyxxz eykBykBxkBxkBH 
 sincossincos 4321
TE Mode
Boundary Conditions
z
oy
z
ox
z
oy
z
ox
e
b
yn
a
xm
H
b
n
h
j
H
e
b
yn
a
xm
H
a
m
h
j
H
e
b
yn
a
xm
H
a
m
h
j
E
e
b
yn
a
xm
H
b
n
h
j
E
























































































sincos
cossin
cossin
sincos
2
2
2
2
0
coscos













 
z
zj
oz
E
ey
b
n
x
a
m
HH 
𝐸 𝑥 = −
𝑗𝜔𝜇
ℎ2
𝜕𝐻 𝑧
𝜕𝑦
𝐻 𝑥 = −
𝛾
ℎ2
𝜕𝐻 𝑧
𝜕𝑥
𝐸 𝑦 = −
𝑗𝜔𝜇
ℎ2
𝜕𝐻 𝑧
𝜕𝑥
𝐻 𝑦 = −
𝛾
ℎ2
𝜕𝐻 𝑧
𝜕𝑦
TE Mode

9. Cut-off Frequency and propagation Constant
• The cutoff frequency occurs when
• Evanescent:
• Means no propagation, everything is attenuated
• Propagation:
• This is the case we are interested since is when the wave is allowed to
travel through the guide.
 



2
22
222














b
n
a
m
kkk yx
When 𝜔𝑐
2 𝜇𝜀 =
𝑚𝜋
𝑎
2
+
𝑛𝜋
𝑏
2
then 𝛾 = 𝛼 + 𝑗𝛽 = 0
or 𝑓𝑐 =
1
2𝜋
1
𝜇𝜀
𝑚𝜋
𝑎
2
+
𝑛𝜋
𝑏
2
When 𝜔2
𝜇𝜀 <
𝑚𝜋
𝑎
2
+
𝑛𝜋
𝑏
2
𝛾 = 𝛼 and 𝛽 = 0
When 𝜔2
𝜇𝜀 >
𝑚𝜋
𝑎
2
+
𝑛𝜋
𝑏
2
𝛾 = 𝑗𝛽 and 𝛼 = 0

10. TE mode E and H Field particle View
TE mode E and H Field Wave Vectors
Figure showing the particle view of the fields
Left side- Electric Field
Right Side- Magnetic Field
Figure showing the Vector view of the fields
Left side- Electric Field
Right Side- Magnetic Field
Field Views inside
Rectangular Waveguide

11. E Field 3D View
Field Views inside
Rectangular Waveguide
TE12 Mode E Field Vectors

12. TE Mode E and H Field
combined View
TE32 Mode E and H Field
Radiation View
Field Views inside
Rectangular Waveguide

13. References
1- commons.wikimedia.org
2- https://www.wikipedia.org
3- documents.pub_rectangular-wave-guides
4- physics stackexchange com
5- manson.gmu.edu
6- http://www.falstad.com/embox/guide.html