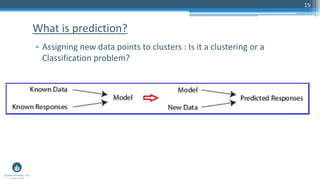
This document summarizes a presentation given by Sri Krishnamurthy on machine learning applications for credit risk. The presentation covered topics such as credit scoring models, traditional credit assessment approaches, peer-to-peer lending, and using clustering algorithms and dimensionality reduction techniques to analyze lending club loan data. Specific clustering and visualization methods discussed include partitioning around medoids, t-distributed stochastic neighborhood embedding, and analyzing mixed data types using Gower similarity coefficients.

1. Location:
QuantUniversity Meetup
October 28th 2016
Boston MA
Machine Learning applications for Credit Risk
2016 Copyright QuantUniversity LLC.
Presented By:
Sri Krishnamurthy, CFA, CAP
www.QuantUniversity.com
sri@quantuniversity.com

2. 2
Slides and Code will be available at:
http://www.analyticscertificate.com

3. - Analytics Advisory services
- Custom training programs
- Architecture assessments, advice and audits

4. • Founder of QuantUniversity LLC. and
www.analyticscertificate.com
• Advisory and Consultancy for Financial Analytics
• Prior Experience at MathWorks, Citigroup and
Endeca and 25+ financial services and energy
customers.
• Regular Columnist for the Wilmott Magazine
• Author of forthcoming book
“Financial Modeling: A case study approach”
published by Wiley
• Charted Financial Analyst and Certified Analytics
Professional
• Teaches Analytics in the Babson College MBA
program and at Northeastern University, Boston
Sri Krishnamurthy
Founder and CEO
4

5. 5
Quantitative Analytics and Big Data Analytics Onboarding
• Trained more than 500 students in
Quantitative methods, Data Science
and Big Data Technologies using
MATLAB, Python and R
• Launching the Analytics Certificate
Program in September

7. 7

8. Credit risk in consumer credit
Credit-scoring models and techniques assess the risk in lending to
customers.
Typical decisions:
• Grant credit/not to new applicants
• Increasing/Decreasing spending limits
• Increasing/Decreasing lending rates
• What new products can be given to existing applicants ?

9. Credit assessment in consumer credit
History :
• Gut feel
• Social network
• Communities and influence
Traditional:
• Scoring mechanisms through credit bureaus
• Bank assessments through business rules
Newer approaches:
• Peer-to-Peer lending
• Prosper Market place

10. 10
• The paper finds a link between
having a high credit score and the
likelihood of both entering into a
committed relationship, and
staying in one.
Credit risk in the news
https://www.federalreserve.gov/econresdata/feds/2015/files/2
015081pap.pdf

11. 11

12. 12

13. 13

14. 14
Another methodology

15. 15
• Assigning new data points to clusters : Is it a clustering or a
Classification problem?
What is prediction?

16. 16
Types of algorithms
Machine
learning
Supervised
Learning
Prediction
Classification
Unsupervised
Learning
Clustering

17. 17
• Features or Dimensions
▫ Attributes of data used for modeling
• Explanatory variables or Independent Variables
• Response Variables or Dependent Variables
Y = F(Xi)
Y = Dependent Variable
Xi = Independent Variables
Terms

18. 18
• Numerical variables
▫ Real
 Temperature : 61.4F, 58F
▫ Integers
 Number of Bedrooms : 2,3,4
• Categorical variables
▫ Binary
 Gas-heat : Yes/No
▫ Nominal : No intrinsic ordering
 Boston, New York, Chicago
▫ Ordinal : Ordered
 Small, Medium, Large
Types of variables

19. 19
Used to derive a relationship between dependent and independent
variables
• Prediction
▫ Regression
▫ Decision Trees (CART)
▫ Neural Networks
• Classification
▫ Logistic Regression
▫ CART, Random Forest, SVM
▫ Neural Networks
Supervised Learning

20. 20
Data pre-
processing
Split Data into
Training and
Testing sets
Train the model
on Training data
Test the model
using Testing data
to evaluate model
performance
Methodology

21. 21
• No distinction between independent variables and dependent
variables
• No result labels to determine “correct” results
• Goals:
▫ Data Reduction
▫ Clustering
Unsupervised Learning

22. 22
• The goal is to find similarities in the training data and to partition
the dataset into subsets that are demarcated by these similarities.
• The clusters are not labeled but the labels are deduced through
review of the members of the clusters.
• Works well when large amounts of data available.
Clustering

23. 23
• Partitioning Clustering
▫ Starts with K –number of clusters sought
▫ Observations randomly divided to form cohesive clusters
▫ Example : K-means
• Hierarchical Agglomerative Clustering
▫ Each observation is its own cluster
▫ Combine clusters two at a time to finally have one cluster
▫ Example: Hierarchical clustering using single linkage, Ward’s method
etc.
Types of Clustering

24. 24
• Tries to separate samples into K groups with a goal of maximizing
between group variance and minimizing within group variance
• Requires K to be specified up front.
• Starts with K initial centroids and optimizes to minimize the criterion
or till the number of specified iterations are reached.
• Suited for larger datasets
• http://shabal.in/visuals/kmeans/3.html
K-means

25. 25
• Goal is to derive a dendrogram starting from each record being its
own cluster
• Works well for smaller data sets
• Proximity is measured in multiple ways (more later)
Hierarchical clustering

26. 26
How do you measure similarity between two entities ?
▫ Apples and Bananas
▫ Coke and Pepsi vs Orange juice
▫ Honda Civic vs Toyota Corolla
▫ New York and Boston
• The notion of distance
The notion of distance

27. 27
• Euclidean distance
• Cosine distance
Distance measures

28. 28
• Manhattan distance
(Taxi-cab distance)
• Jaccard distance
▫ Used to measure similarity or dissimilarity between binary and non-
binary variables
▫ http://people.revoledu.com/kardi/tutorial/Similarity/Jaccard.html
Other distance measures

29. 29
• Gower similarity coefficient is a composite measure
• It takes quantitative (such as rating scale), binary (such as
present/absent) and nominal (such as worker/teacher/clerk) variables.
• Gower distance is used for calculating distances when we have mixed
types of variables (continuous and categorical)
• A linear combination using user-specified weights (most simple an
average) is calculated to create the final distance matrix.
• The metrics used for each data type are described below:
▫ Quantitative: range-normalized Manhattan distance
▫ Ordinal: variable is first ranked, then Manhattan distance is used with a
special adjustment for ties
▫ Nominal: variables of k categories are first converted into k binary columns
and then the Dice coefficient is used
(https://en.wikipedia.org/wiki/S%C3%B8rensen%E2%80%93Dice_coefficient
)
Working with mixed-data

30. 30
• daisy
• Pam
• agnes
https://stat.ethz.ch/R-manual/R-devel/library/cluster/html/pam.html
https://en.wikibooks.org/wiki/Data_Mining_Algorithms_In_R/Clusteri
ng/CLARA
Support in R

31. 31

32. 32
Lending club

33. 33
The Data
https://www.lendingclub.com/info/download-data.action

34. 34
The Data
https://www.kaggle.com/wendykan/lending-club-loan-data

35. Variable description

36. • Calculate dissimilarity between observations.
• Select algorithm to group observations together
• Choose the best number of clusters
• Visualize clusters on reduced dimensions
Objective

37. • Partitioning around medoids (PAM) is used in this case.
• PAM is an iterative clustering procedure with the following steps:
▫ Step 1: Choose k random entities to become the medoids.
▫ Step 2: Assign every entity to its closest medoid (using the distance
matrix we have calculated).
▫ Step 3: For each cluster, identify the observation that would yield the
lowest average distance if it were to be re-assigned as the medoid. If
so, make this observation the new medoid.
▫ Step 4: If at least one medoid has changes, return to step 2.
Otherwise, end the algorithm.
Selecting number of clusters

38. • One way to visualize many variables in a lower dimensional space is
with t-distributed stochastic neighborhood embedding (t-SNE)
• This method is a dimension reduction technique that tries to
preserve local structure so as to make clusters visible in a 2D or 3D
visualization.
• https://en.wikipedia.org/wiki/T-
distributed_stochastic_neighbor_embedding
Visualization with reduced dimension

39. Thank you!
Members & Sponsors!
Sri Krishnamurthy, CFA, CAP
Founder and CEO
QuantUniversity LLC.
srikrishnamurthy
www.QuantUniversity.com
Contact
Information, data and drawings embodied in this presentation are strictly a property of QuantUniversity LLC. and shall not be
distributed or used in any other publication without the prior written consent of QuantUniversity LLC.
39