Andrea Gigli, profile picture
Uploaded byAndrea Gigli
PPTX, PDF2,045 views

Feature Selection for Document Ranking

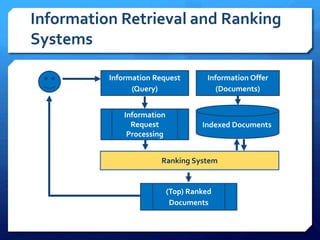
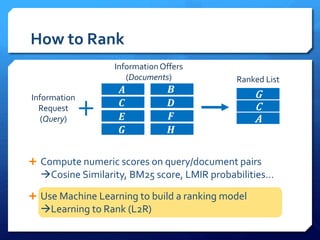
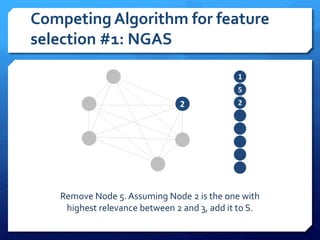
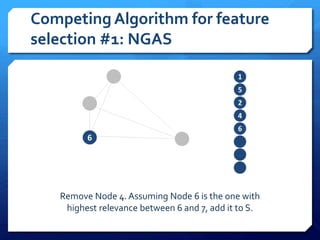
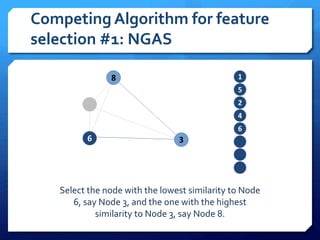
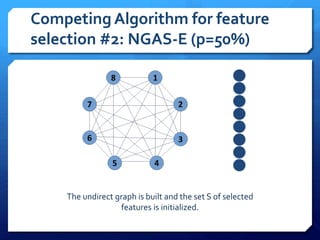
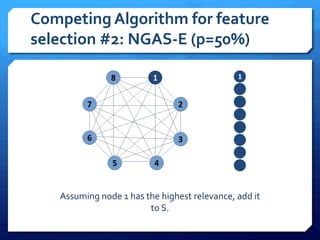
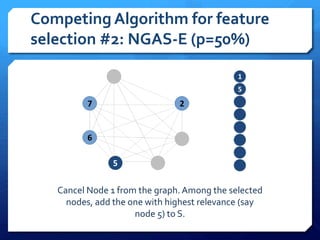
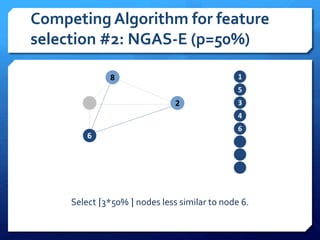
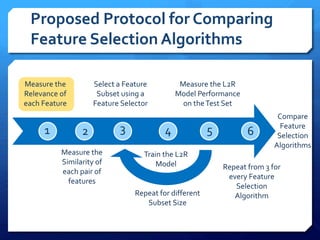
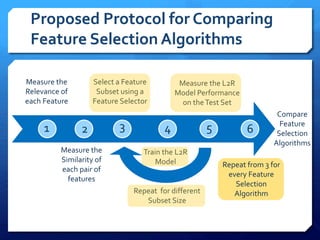
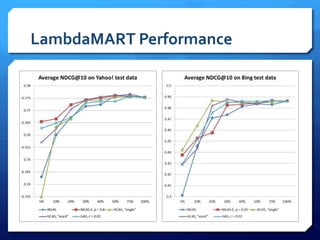
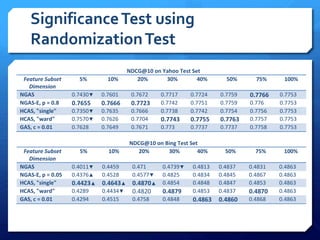
The document discusses feature selection algorithms for learning to rank, focusing on proposed feature selection protocols and their application to publicly available web search data. It outlines various competing algorithms including naive greedy search and hierarchical clustering, detailing methods to measure feature relevance and selection performance. Additionally, it describes machine learning strategies for ranking and provides insights into the operational mechanics of ranking systems and their evaluation metrics.

Embed presentation

Downloaded 86 times
Feature Selection Algorithms for Learning to Rank Andrea Gigli Email Slides: http://www.slideshare.net/andrgig March-2016
Outline  Machine Learning for Ranking  Proposed Feature Selection Algorithms (FSA) and Feature Selection Protocol  Application to Public Available Web Search Data
Outline  Machine Learning for Ranking  Proposed Feature Selection Algorithms (FSA) and Feature Selection Protocol  Application to Public Available Web Search Data
Information Retrieval and Ranking Systems  Information Retrieval is the activity of providing information offers relevant to an information need from a collection of information resources.  Ranking consists in sorting the information offers according to some criterion, so that the "best" results appear early in the provided list.
Information Retrieval and Ranking Systems Ranking System Information Request (Query) Information Offer (Documents) Indexed Documents Information Request Processing (Top) Ranked Documents
 Compute numeric scores on query/document pairs Cosine Similarity, BM25 score, LMIR probabilities…  Use Machine Learning to build a ranking model Learning to Rank (L2R) How to Rank 𝑨 𝑪 𝑩 G C A 𝑫 Information Offers (Documents) Ranked List Information Request (Query) 𝑬 𝑮 𝑭 𝑯
… … ... ... Learning System Ranking System Indexed Documents ... Training Prediction How to Rank using Supervised Learning ... ... 𝑑1,1 𝑑1,2 ℓ1,1 𝑑1,𝑁1 ℓ1,2 ℓ1,𝑁1 … … 𝑑M,1 𝑑M,2 ℓ 𝑀,1 𝑑M,𝑁 𝑀 ℓ 𝑀,2 ℓ 𝑀,𝑁2 𝑞1 𝑞 𝑀 𝑓(𝑞, 𝑑) 𝑞 𝑀+1 𝑓(𝑞 𝑀+1, 𝑑 𝑁1 ) 𝑓(𝑞 𝑀+1, 𝑑 𝑁 𝑀 ) 𝑞𝑖: i-th query 𝑑𝑖,𝑗: j-th document associated to the i-th query ℓ𝑖,𝑗: observed score of the j-th document associated to the i-th query 𝑓(𝒒, 𝒐): scoring function
Machine Learning for Ranking Documents: Application Fields
Machine Learning for Ranking Documents: Business Cases
Outline  Machine Learning for Ranking  Proposed Feature Selection Algorithms (FSA) and Feature Selection Protocol  Application to Public Available Web Search Data
Query & Information Offer Features 𝑑𝑖,1 𝑑𝑖,2 𝑑𝑖,𝑁 𝑖𝑞𝑖 … …ℓ𝑖,1 ℓ𝑖,2 ℓ𝑖,𝑁 𝑖 𝑥𝑖,1 (1) 𝑥𝑖,1 (2) 𝑥𝑖,1 (3) ⋮ 𝑥𝑖,1 (𝐹) 𝑥𝑖,2 (1) 𝑥𝑖,2 (2) 𝑥𝑖,2 (3) ⋮ 𝑥𝑖,2 (𝐹) 𝑥𝑖,𝑁 𝑖 (1) 𝑥𝑖,𝑁 𝑖 (2) 𝑥𝑖,𝑁 𝑖 (3) ⋮ 𝑥𝑖,𝑁 𝑖 (𝐹) … Documents Query/Documents LabelsQuery  𝑓 𝒒, 𝒐 → 𝑓(𝒙)  F is of the order of hundreds, thousands
Which features Case Feature examples Web Search Query-URL matching features: number of occurrences of query terms in the document, BM25, N-gram BM25,Tf-Idf,… Importance of Url: PageRank , Number of in-links, Number of clicks, Browse Rank, Spam Score, Page Quality Score………….. Online Advertisement User features: last page visited, time from the last visit, last advertisement clicked, products queried… Product features: product description, product category, price… User-product matching feature: tf-idf, expected rating,… Page-Product matching feature: topic, category, tf-idf, … Collaborative Filtering User features: age, gender, consumption history, … Product characteristics: category, price, description, … Context - Product matching: tag-matching, tf-idf, … … …
How to select features in L2R  The main goal of any feature selection process is to select a subset of n elements from a set of N measurement, with n<N, without significantly degrading the performance of the system  The search for the optimal subset require to search among 2N possible subsets
How to select features in L2R 0 1,000,000 2,000,000 3,000,000 4,000,000 5,000,000 6,000,000 7,000,000 8,000,000 9,000,000 0 5 10 15 20 25 Number of possible feature subsets Number of Features A suboptimal criteria is needed
Proposed Protocol for Comparing Feature Selection Algorithms Measure the Relevance of each Feature Measure the Similarity of each pair of features Select a Feature Subset using a Feature Selector Train the L2R Model Measure the L2R Model Performance on theTest Set Compare Feature Selection Algorithms Repeat for different Subset Size 1 2 3 4 5 6 Repeat from 3 for every Feature Selection Algorithm
Competing Algorithms for feature selection We developed the following algorithms  Naïve Greedy searchAlgorithm for feature Selection (NGAS)  Naïve Greedy searchAlgorithm for feature Selection - Extended (NGAS-E)  Hierarchical Clustering search Algorithm for feature Selection (HCAS)
Competing Algorithms for feature selection We developed the following algorithms  Naïve Greedy searchAlgorithm for feature Selection (NGAS)  Naïve Greedy searchAlgorithm for feature Selection - Extended (NGAS-E)  Hierarchical Clustering search Algorithm for feature Selection (HCAS)
Competing Algorithm for feature selection #1: NGAS The undirect graph is built and the set S of selected features is initialized.
Competing Algorithm for feature selection #1: NGAS Assuming node 1 has the highest relevance, add it to S.
Competing Algorithm for feature selection #1: NGAS Select the node with the lowest similarity to Node 1, say Node 7, and the one with the highest similarity to Node 7, say Node 5.
Competing Algorithm for feature selection #1: NGAS Remove Node 1. Node 5 is the one with the highest relevance between 5 and 7, add it to S.
Competing Algorithm for feature selection #1: NGAS Select the node with the lowest similarity to Node 5, say Node 2, and the one with the highest similarity to Node 2, say Node 3.
Competing Algorithm for feature selection #1: NGAS Remove Node 5. Assuming Node 2 is the one with highest relevance between 2 and 3, add it to S.
Competing Algorithm for feature selection #1: NGAS Select the node with the lowest similarity to Node 2, say Node 4, and the one with the highest similarity to Node 4, say Node 8.
Competing Algorithm for feature selection #1: NGAS Remove Node 2. Assuming Node 4 is the one with highest relevance between 4 and 8, add it to S.
Competing Algorithm for feature selection #1: NGAS Select the node with the lowest similarity to Node 4, say Node 6, and the one with the highest similarity to Node 6, say Node 7.
Competing Algorithm for feature selection #1: NGAS Remove Node 4. Assuming Node 6 is the one with highest relevance between 6 and 7, add it to S.
Competing Algorithm for feature selection #1: NGAS Select the node with the lowest similarity to Node 6, say Node 3, and the one with the highest similarity to Node 3, say Node 8.
Competing Algorithm for feature selection #1: NGAS Remove Node 6. Assuming Node 3 is the one with highest relevance between 3 and 8, add it to S.
Competing Algorithm for feature selection #1: NGAS Select the node with the lowest similarity to Node 3, say Node 8, and the one with the highest similarity to Node 8, say Node 7.
Competing Algorithm for feature selection #1: NGAS Remove Node 3. Assuming Node 8 is the one with highest relevance between 8 and 7, add it to S.
Competing Algorithm for feature selection #1: NGAS Add the last node, 7, to S.
We developed the following algorithms  Naïve Greedy searchAlgorithm for feature Selection (NGAS)  Naïve Greedy searchAlgorithm for feature Selection - Extended (NGAS-E)  Hierarchical Clustering search Algorithm for feature Selection (HCAS) Competing Algorithms for feature selection
Competing Algorithm for feature selection #2: NGAS-E (p=50%) The undirect graph is built and the set S of selected features is initialized.
Competing Algorithm for feature selection #2: NGAS-E (p=50%) Assuming node 1 has the highest relevance, add it to S.
Competing Algorithm for feature selection #2: NGAS-E (p=50%) Select 7 ∗ 50% nodes less similar to 1.
Competing Algorithm for feature selection #2: NGAS-E (p=50%) Cancel Node 1 from the graph. Among the selected nodes, add the one with highest relevance (say node 5) to S.
Competing Algorithm for feature selection #2: NGAS-E (p=50%) Select ⌈6*50% ⌉ nodes less similar to node 5.
Competing Algorithm for feature selection #2: NGAS-E (p=50%) Cancel Node 5 from the graph. Among the selected nodes, add the one with highest relevance (say Node 3) to S.
Competing Algorithm for feature selection #2: NGAS-E (p=50%) Select ⌈5*50% ⌉ nodes less similar to node 3.
Competing Algorithm for feature selection #2: NGAS-E (p=50%) Cancel node 3 from the graph. Among the selected nodes, add the one with highest relevance (say node 4) to S.
Competing Algorithm for feature selection #2: NGAS-E (p=50%) Select ⌈4*50% ⌉ nodes less similar to node 4.
Competing Algorithm for feature selection #2: NGAS-E (p=50%) Cancel node 4 from the graph. Among the selected nodes, add the one with highest relevance (say node 6) to S.
Competing Algorithm for feature selection #2: NGAS-E (p=50%) Select ⌈3*50% ⌉ nodes less similar to node 6.
Competing Algorithm for feature selection #2: NGAS-E (p=50%) Cancel node 6 from the graph. Among the selected nodes, add the one with highest relevance (say node 2) to S.
Competing Algorithm for feature selection #2: NGAS-E (p=50%) Select ⌈2*50% ⌉nodes less similar to node 2.
Competing Algorithm for feature selection #2: NGAS-E (p=50%) Node 2 is cancelled from the graph and node 8 is added to S.
Competing Algorithm for feature selection #2: NGAS-E (p=50%) Node 8 is cancelled from the graph and the last node, 7, is added to S.
Competing Algorithm for feature selection #2: NGAS-E (p=50%) Node 8 is cancelled from the graph and the last node, 7, is added to S.
We developed the following algorithms  Naïve Greedy searchAlgorithm for feature Selection (NGAS)  Naïve Greedy searchAlgorithm for feature Selection - Extended (NGAS-E)  Hierarchical Clustering search Algorithm for feature Selection (HCAS) Competing Algorithms for feature selection
Competing Algorithm for feature selection #3: HCAS 23 11 5 3
Outline  Machine Learning for Ranking  Proposed Feature Selection Algorithms (FSA) and Feature Selection Protocol  Application to Public Available Web Search Data
Application to Web Search Engine Data  Bing Data http://research.microsoft.com/en-us/projects/mslr/  Yahoo! Data http://webscope.sandbox.yahoo.com Train Validation Test #queries 19,944 2,994 6,983 #urls 473,134 71,083 165,660 # features 519 Train Validation Test #queries 18,919 6,306 6,306 #urls 723,412 235,259 241,521 # features 136
Proposed Protocol for Comparing Feature Selection Algorithms Measure the Relevance of each Feature Measure the Similarity of each pair of features Select a Feature Subset using a Feature Selector Train the L2R Model Measure the L2R Model Performance on theTest Set Compare Feature Selection Algorithms Repeat for different Subset Size 1 2 3 4 5 6 Repeat from 3 for every Feature Selection Algorithm
Learning to Rank Algorithms: a timeline of major contributions LambdaMART LambdaRank CRR IntervalRank GBlend NDCG Boost BayesRank BoltzRank MPBoost SortNet SSRankBoost RR SoftRank PermuRank ListMLE SVMmap RankRLS RankGP RankCosine QBRank McRank ListNet GBRank AdaRank IR-SVM RankNet RankBoost Pranking RankSVM 2000 2002 2003 2005 2006 2007 FRank 2008 2009 2010 Pointwise Pairwise Listwise
Multiple Additive Regression Trees LambdaMART Model for LtR Lambda function  Ensemble method:Tree Boosting  Loss function not differentiable  Sorting characteristic  Speed
Proposed Protocol for Comparing Feature Selection Algorithms Measure the Relevance of each Feature Measure the Similarity of each pair of features Select a Feature Subset using a Feature Selector Train the L2R Model Measure the L2R Model Performance on theTest Set Compare Feature Selection Algorithms Repeat for different Subset Size 1 2 3 4 5 6 Repeat from 3 for every Feature Selection Algorithm
Feature Relevance  The relevance of a document is measured with a categorical variable (0,1,2,3,4)  we need to use metrics good at measuring «dependence» between discrete/continuous feature variables and a categorical label variable.  In the following we use  Normalized Mutual Information (NMI):  Spearman coefficient (S)  Kendall’s tau (K)  Average GroupVariance (AGV)  OneVariable NDCG@10 (1VNDCG)
Feature Relevance via Normalized Mutual Information  Mutual Information (MI) measures how much, on average, the realization of a random variable X tells us about the realization of the random variableY, or how much the entropy ofY, H(Y), is reduced knowing about the realization of X 𝑀𝐼 𝑋, 𝑌 = 𝐻 𝑋 − 𝐻 𝑋 𝑌 = 𝐻 𝑋 + 𝐻 𝑌 − 𝐻 𝑋, 𝑌 The normalizad version is 𝑁𝑀𝐼 𝑋, 𝑌 = 𝑀𝐼(𝑋, 𝑌) 𝐻(𝑋) 𝐻(𝑌)
Feature Relevance via Spearman’s coefficient  Spearman’s rank correlation coefficient is a non-parametric measure of statistical dependence between two random variables. It is given by 𝜌 = 1 − 6 𝑑𝑖 2 𝑛(𝑛2 − 1) where n is the sample size and 𝑑𝑖 = 𝑟𝑎𝑛𝑘 𝑥𝑖 − 𝑟𝑎𝑛𝑘 𝑦𝑖
Feature Relevance via Kendall’s tau  Kendall’sTau is a measure of association defined on two ranking lists of length n. It is defined as τ = 𝑛 𝑐 − 𝑛 𝑑 𝑛(𝑛 − 1) 2 − 𝑛1 𝑛(𝑛 − 1) 2 − 𝑛2 where 𝑛 𝑐 denotes the number of concordant pairs between the two lists, 𝑛 𝑑 denotes the number of discordant pairs, 𝑛1 = 𝑡𝑖(𝑡𝑖 − 1)/2, 𝑛2 = 𝑢𝑗(𝑢𝑗 − 1)/2, 𝑡𝑖 is the number of tied values in the i-th group of ties for the first list and 𝑢𝑗 is the number of tied values in the j-th group of ties for the second list.
Feature Relevance via Average GroupVariance  Average GroupVariance measure the discrimination power of a feature.The intuitive justification is that a feature is useful if it is capable of discriminating a small portion of the ordered scale from the rest, and that features with a small variance are those which satisfy this property. 𝐴𝐺𝑉 = 1 − 𝑔=1 5 𝑛 𝑔 𝑥 𝑔 − 𝑥 2 𝑖 𝑥𝑖 − 𝑥 2 where 𝑛 𝑔be the size of group g, 𝑥 𝑔 the sample mean of feature 𝑥 in the g-th group and 𝑥 whole sample mean.
Feature Relevance via single feature LambdaMART scoring  For each feature i we run LambdaMART and compute the 𝑁𝐷𝐶𝐺𝑖,𝑞@10 for each query q  The i-th feature relevance is measured averaging 𝑁𝐷𝐶𝐺𝑖,𝑞@10 over the whole query set 𝑁𝐷𝐶𝐺𝑖@10 = 1 𝑄 𝑞∈𝑄 𝑁𝐷𝐶𝐺𝑖,𝑞@10
 Precision at k: 𝑃𝑖@𝑘 = # 𝑟𝑒𝑙𝑒𝑣𝑎𝑛𝑡 𝑑𝑜𝑐𝑢𝑚𝑒𝑛𝑡𝑠 𝑖𝑛 𝑡𝑜𝑝 𝑘 𝑟𝑒𝑠𝑢𝑙𝑡𝑠 𝑘  Average precision: 1 𝐷 𝑘=1 𝐷 𝑃𝑖@𝑘 ∙ 𝕀 𝑑𝑜𝑐𝑢𝑚𝑒𝑛𝑡 𝑘 𝑖𝑠 𝑟𝑒𝑙𝑒𝑣𝑎𝑛𝑡 # 𝑟𝑒𝑙𝑒𝑣𝑎𝑛𝑡 𝑑𝑜𝑐𝑢𝑚𝑒𝑛𝑡𝑠  Discounted Cumulative Gain 𝐷𝐶𝐺𝑖 = 𝑗=1 𝑘 2 𝑟𝑒𝑙 𝑖,𝑗 − 1 𝑙𝑜𝑔2 1 + 𝑟𝑎𝑛𝑘𝑗 How to Measure Ranking Performance on query i
How to Measure Ranking Performance: Normalized DCG Document Gain Cumulative Gain Document 1 31 31 Document 2 3 34 Document 3 7 41 Document 4 31 72 Discounted 31x1=31 31+3x0.63=32.9 32.9+7x0.5=36.4 36.4+31x0.4=48.8 Normalization: divide DCG by the ideal DCG Document Gain Cumulative Gain Document 1 31 31 Document 4 31 62 Document 3 7 69 Document 2 3 72 Discounted 31x1=31 31+31x0.63=50.53 50.53+7x0.5=54.03 54.03+3x0.4=57.07 Relevance Rating Gain Perfect 25-1=31 Excellent 24-1=15 Good 23-1=7 Fair 22-1=3 Bad 21-1=1
Feature Relevance
Feature Relevance
Choosing the Relevance Measure (1/2) FSA performance is measured using the Average NDCG@10 obtaind from LambdaMART on the test set. NDCG@10 on Yahoo Test Set Feature Subset Dimension 5% 10% 20% 30% 40% 50% 75% 100% NMI 0.73398 0.75952 0.76241 0.7678 0.76912 0.769 0.77015 0.76935 AVG 0.7524 0.7548 0.76168 0.76493 0.76498 0.76717 0.76971 0.76935 S 0.74963 0.75396 0.76099 0.76398 0.7649 0.76753 0.77002 0.76935 K 0.75225 0.75291 0.76145 0.76304 0.7648 0.76673 0.76972 0.76935 1VNDCG 0.75246 0.75768 0.76452 0.76672 0.76823 0.77008 0.77027 0.76935 NDCG@10 on Bing Test Set Feature Subset Dimension 5% 10% 20% 30% 40% 50% 75% 100% NMI 0.38927 0.3978 0.41347 0.41539 0.44785 0.44966 0.45083 0.46336 AVG 0.32682 0.33168 0.36043 0.36976 0.37383 0.37612 0.43444 0.46336 S 0.32969 0.3346 0.3428 0.34592 0.36711 0.42475 0.42809 0.46336 K 0.32917 0.3346 0.34356 0.42124 0.42071 0.4245 0.42706 0.46336 1VNDCG 0.41633 0.42571 0.42413 0.42601 0.42757 0.43795 0.46222 0.46336
Choosing the Relevance Measure (2/2)
Proposed Protocol for Comparing Feature Selection Algorithms Measure the Relevance of each Feature Measure the Similarity of each pair of features Select a Feature Subset using a Feature Selector Train the L2R Model Measure the Model Performance on theTest Set Compare Feature Selection Algorithms Repeat for different Subset Size 1 2 3 4 5 6 Repeat from 3 for every Feature Selection Algorithm
Feature Similarity  We used Spearman’s Rank coefficient for measuring features similarity.  Spearman’s Rank is faster to be computed than NMI, Kendall’s tau and 1VNDCG.
The FSA benchmark: Greedy Algorithm for feature Selection 1. Build a complete undirected graph 𝐺0, in which a) each node represent the i-th feature with weight 𝑤𝑖 and b) each edge has weigth 𝑒𝑖,𝑗 2. Let 𝑆0 = ∅ be the set of selected features at step 0. 3. For i=1, …, n a) Select the node with largest weight from 𝐺𝑖−1, suppose that it is the k- th node b) Punish all the nodes connected with the k-th node: 𝑤𝑗 ← 𝑤𝑗 −2*c*𝑒 𝑘,𝑗, 𝑗 ≠ 𝑘 c) Add the k-th node to 𝑆𝑖−1 d) Remove the k-th node from 𝐺𝑖−1 4. Return 𝑆 𝑛
Train the L2R Model Proposed Protocol for Comparing Feature Selection Algorithms Measure the Relevance of each Feature Measure the Similarity of each pair of features Select a Feature Subset using a Feature Selector Compare Feature Selection Algorithms Repeat for different Subset Size 1 2 3 4 5 6 Repeat from 3 for every Feature Selection Algorithm Measure the L2R Model Performance on theTest Set
Proposed Protocol for Comparing Feature Selection Algorithms Measure the Relevance of each Feature Measure the Similarity of each pair of features Select a Feature Subset using a Feature Selector Train the L2R Model Measure the L2R Model Performance on theTest Set Compare Feature Selection Algorithms 1 2 3 4 5 6 Repeat from 3 for every Feature Selection AlgorithmRepeat for different Subset Size
Proposed Protocol for Comparing Feature Selection Algorithms Measure the Relevance of each Feature Measure the Similarity of each pair of features Select a Feature Subset using a Feature Selector Train the L2R Model Compare Feature Selection Algorithms Repeat for different Subset Size 1 2 3 4 5 6 Repeat from 3 for every Feature Selection Algorithm Measure the Model Performance on theTest Set
LambdaMART Performance
SignificanceTest using RandomizationTest NDCG@10 on Yahoo Test Set Feature Subset Dimension 5% 10% 20% 30% 40% 50% 75% 100% NGAS 0.7430▼ 0.7601 0.7672 0.7717 0.7724 0.7759 0.7766 0.7753 NGAS-E, p = 0.8 0.7655 0.7666 0.7723 0.7742 0.7751 0.7759 0.776 0.7753 HCAS, "single" 0.7350▼ 0.7635 0.7666 0.7738 0.7742 0.7754 0.7756 0.7753 HCAS, "ward" 0.7570▼ 0.7626 0.7704 0.7743 0.7755 0.7763 0.7757 0.7753 GAS, c = 0.01 0.7628 0.7649 0.7671 0.773 0.7737 0.7737 0.7758 0.7753 NDCG@10 on Bing Test Set Feature Subset Dimension 5% 10% 20% 30% 40% 50% 75% 100% NGAS 0.4011▼ 0.4459 0.471 0.4739▼ 0.4813 0.4837 0.4831 0.4863 NGAS-E, p = 0.05 0.4376▲ 0.4528 0.4577▼ 0.4825 0.4834 0.4845 0.4867 0.4863 HCAS, "single" 0.4423▲ 0.4643▲ 0.4870▲ 0.4854 0.4848 0.4847 0.4853 0.4863 HCAS, "ward" 0.4289 0.4434▼ 0.4820 0.4879 0.4853 0.4837 0.4870 0.4863 GAS, c = 0.01 0.4294 0.4515 0.4758 0.4848 0.4863 0.4860 0.4868 0.4863
LambdaMART Performance
Conclusions  We designed 3 FSAs and we applied them to the Web Search Pages Ranking problem.  NGAS-E e HCAS have a performance equal or greater than the benchmark model.  HCAS and NGAS are very  The proposed FSAs can be implemented independently of the L2R model.  The proposed FSAs can be applied to other ML contexts, to Sorting problems and to Model Ensambling.
Thanks! Andrea Gigli Slides: http://www.slideshare.net/andrgig

More Related Content

PDF
Feature selection
byDong Guo
 
PPTX
Feature selection
bydkpawar
 
PPTX
Using SHAP to Understand Black Box Models
byJonathan Bechtel
 
PDF
Fast Feature Selection for Learning to Rank - ACM International Conference on...
byAndrea Gigli
 
PDF
Master in Big Data Analytics and Social Mining 20015
byAndrea Gigli
 
PPT
probabilistic ranking
byFELIX75
 
PDF
Scaling Analytics with Apache Spark
byQuantUniversity
 
PDF
Hybridisation Techniques for Cold-Starting Context-Aware Recommender Systems
byMatthias Braunhofer
 
Feature selection
byDong Guo
 
Feature selection
bydkpawar
 
Using SHAP to Understand Black Box Models
byJonathan Bechtel
 
Fast Feature Selection for Learning to Rank - ACM International Conference on...
byAndrea Gigli
 
Master in Big Data Analytics and Social Mining 20015
byAndrea Gigli
 
probabilistic ranking
byFELIX75
 
Scaling Analytics with Apache Spark
byQuantUniversity
 
Hybridisation Techniques for Cold-Starting Context-Aware Recommender Systems
byMatthias Braunhofer
 

What's hot

PDF
Real-world News Recommender Systems
bykib_83
 
PDF
Doctoral Thesis Dissertation 2014-03-20 @PoliMi
byDavide Chicco
 
PPTX
Recommendation Engine Powered by Hadoop
byPranab Ghosh
 
PDF
Neural Networks made easy
byVenkata Reddy Konasani
 
PDF
OpenML NeurIPS2018
byJoaquin Vanschoren
 
PDF
OpenML 2019
byJoaquin Vanschoren
 
PDF
Exposé Ontology
byJoaquin Vanschoren
 
PPTX
Machine learning with scikitlearn
byPratap Dangeti
 
PDF
Testing of Cyber-Physical Systems: Diversity-driven Strategies
byLionel Briand
 
PPTX
Using Negative Detectors for Identifying Adversarial Data Manipulation in Mac...
byKishor Datta Gupta
 
DOCX
Quiz2 cs141-1-17
byFahadaio
 
PPTX
Review Mining of Products of Amazon.com
byShobhit Monga
 
PPT
Chap07
byTerry Yoast
 
PDF
Credit risk meetup
byQuantUniversity
 
PDF
Visualizing the model selection process
byRebecca Bilbro
 
PDF
Open and Automated Machine Learning
byJoaquin Vanschoren
 
PDF
Data exploration validation and sanitization
byVenkata Reddy Konasani
 
PDF
Parallel Tuning of Machine Learning Algorithms, Thesis Proposal
byGianmario Spacagna
 
PDF
Recsys 2016: Modeling Contextual Information in Session-Aware Recommender Sys...
byBartlomiej Twardowski
 
PDF
Yellowbrick: Steering machine learning with visual transformers
byRebecca Bilbro
 
Real-world News Recommender Systems
bykib_83
 
Doctoral Thesis Dissertation 2014-03-20 @PoliMi
byDavide Chicco
 
Recommendation Engine Powered by Hadoop
byPranab Ghosh
 
Neural Networks made easy
byVenkata Reddy Konasani
 
OpenML NeurIPS2018
byJoaquin Vanschoren
 
OpenML 2019
byJoaquin Vanschoren
 
Exposé Ontology
byJoaquin Vanschoren
 
Machine learning with scikitlearn
byPratap Dangeti
 
Testing of Cyber-Physical Systems: Diversity-driven Strategies
byLionel Briand
 
Using Negative Detectors for Identifying Adversarial Data Manipulation in Mac...
byKishor Datta Gupta
 
Quiz2 cs141-1-17
byFahadaio
 
Review Mining of Products of Amazon.com
byShobhit Monga
 
Chap07
byTerry Yoast
 
Credit risk meetup
byQuantUniversity
 
Visualizing the model selection process
byRebecca Bilbro
 
Open and Automated Machine Learning
byJoaquin Vanschoren
 
Data exploration validation and sanitization
byVenkata Reddy Konasani
 
Parallel Tuning of Machine Learning Algorithms, Thesis Proposal
byGianmario Spacagna
 
Recsys 2016: Modeling Contextual Information in Session-Aware Recommender Sys...
byBartlomiej Twardowski
 
Yellowbrick: Steering machine learning with visual transformers
byRebecca Bilbro
 

Viewers also liked

PDF
Libro de-mantenimiento-industrial
byJorge Gamarra Tolentino
 
PDF
Capacitacion y adiestramiento
byDaniel Delgado Esquivel
 
PDF
Onderzoeksrapport acrs v3.0_definitief
byrloggen
 
PDF
Rodriguez alvarez
byRoxana Saldaña
 
PDF
El emprendedor y el empresario profesional cert
byMaestros Online
 
PDF
Estrategias competitivas básicas
byLarryJimenez
 
PDF
Gfpi f-019 guia de aprendizaje 01 tda orientar fpi
bylisbet bravo
 
PPT
3. Your next holiday destination ACTIVIDAD 3 SEMANA 3 ENGLISH DOT WORKS 2.
by.. ..
 
DOCX
Como hacer un plan de negocios
byXPINNERPablo
 
DOC
Evidence: Planning my trip. ENGLISH DOT WORKS 2. SENA. semana 4 actividad 1.
by.. ..
 
DOC
Evidence: Going to the restaurant . ENGLISH DOT WORKS 2. SENA.
by.. ..
 
DOC
Evidence: I can’t believe it.ENGLISH DOT WORKS 2. semana 3 actividad 1.SENA.
by.. ..
 
DOC
Evidence: Describing my kitchen. ENGLISH DOT WORKS 2. SENA.
by.. ..
 
DOC
3.Evidence: Getting to Bogota.ENGLISH DOT WORKS 2. SENA.semana 4 actividad 3.
by.. ..
 
DOC
2. describing cities and places. ENGLISH DOT WORKS 2. SENA. semana 4 acitivda...
by.. ..
 
DOCX
Evidence: Memorable moments.ENGLISH DOT WORKS 2. SENA. semana 2 actividad 2.
by.. ..
 
PPT
Schrijven voor het web
bySimone Levie
 
PDF
Cápsula 1. estudios de mercado
byAudias Torres Coronel
 
PPT
JULIOPARI - Elaborando un Plan de Negocios
byJulio Pari
 
PPTX
C:\Fakepath\Christie
byNerissaemerald
 
Libro de-mantenimiento-industrial
byJorge Gamarra Tolentino
 
Capacitacion y adiestramiento
byDaniel Delgado Esquivel
 
Onderzoeksrapport acrs v3.0_definitief
byrloggen
 
Rodriguez alvarez
byRoxana Saldaña
 
El emprendedor y el empresario profesional cert
byMaestros Online
 
Estrategias competitivas básicas
byLarryJimenez
 
Gfpi f-019 guia de aprendizaje 01 tda orientar fpi
bylisbet bravo
 
3. Your next holiday destination ACTIVIDAD 3 SEMANA 3 ENGLISH DOT WORKS 2.
by.. ..
 
Como hacer un plan de negocios
byXPINNERPablo
 
Evidence: Planning my trip. ENGLISH DOT WORKS 2. SENA. semana 4 actividad 1.
by.. ..
 
Evidence: Going to the restaurant . ENGLISH DOT WORKS 2. SENA.
by.. ..
 
Evidence: I can’t believe it.ENGLISH DOT WORKS 2. semana 3 actividad 1.SENA.
by.. ..
 
Evidence: Describing my kitchen. ENGLISH DOT WORKS 2. SENA.
by.. ..
 
3.Evidence: Getting to Bogota.ENGLISH DOT WORKS 2. SENA.semana 4 actividad 3.
by.. ..
 
2. describing cities and places. ENGLISH DOT WORKS 2. SENA. semana 4 acitivda...
by.. ..
 
Evidence: Memorable moments.ENGLISH DOT WORKS 2. SENA. semana 2 actividad 2.
by.. ..
 
Schrijven voor het web
bySimone Levie
 
Cápsula 1. estudios de mercado
byAudias Torres Coronel
 
JULIOPARI - Elaborando un Plan de Negocios
byJulio Pari
 
C:\Fakepath\Christie
byNerissaemerald
 

Similar to Feature Selection for Document Ranking

PPTX
Feature selection concepts and methods
byReza Ramezani
 
PPT
Nbvtalkonfeatureselection
byNagasuri Bala Venkateswarlu
 
PPT
few common Feature of Size Datum Features are bores, cylinders, slots, or tab...
byDrPArivalaganASSTPRO
 
PPT
feature selection slides share and types of features selection
byQareenasadiq
 
PDF
Feature Selection.pdf
byadarshbarnwal5
 
PDF
International Journal of Engineering Research and Development (IJERD)
byIJERD Editor
 
PDF
Optimization Technique for Feature Selection and Classification Using Support...
byIJTET Journal
 
PPTX
Bu-Refresher course PRESENTATION NEW.pptx
bysrideviramaraj2
 
PDF
Network Based Intrusion Detection System using Filter Based Feature Selection...
byIRJET Journal
 
PDF
Study on Relavance Feature Selection Methods
byIRJET Journal
 
PDF
Iaetsd an efficient and large data base using subset selection algorithm
byIaetsd Iaetsd
 
PDF
International Journal of Engineering Research and Development (IJERD)
byIJERD Editor
 
PDF
IRJET- Survey of Feature Selection based on Ant Colony
byIRJET Journal
 
PPT
6811067.ppt6811067.ppt6811067.ppt6811067.ppt
bynagalakshmig4
 
PDF
The International Journal of Engineering and Science (The IJES)
bytheijes
 
DOCX
A fast clustering based feature subset selection algorithm for high-dimension...
byIEEEFINALYEARPROJECTS
 
DOCX
JAVA 2013 IEEE DATAMINING PROJECT A fast clustering based feature subset sele...
byIEEEGLOBALSOFTTECHNOLOGIES
 
PDF
Feature Selection Algorithm for Supervised and Semisupervised Clustering
byEditor IJCATR
 
PDF
A Survey and Comparative Study of Filter and Wrapper Feature Selection Techni...
bytheijes
 
PPT
SEO PROCESS
byMohan Balakrishna
 
Feature selection concepts and methods
byReza Ramezani
 
Nbvtalkonfeatureselection
byNagasuri Bala Venkateswarlu
 
few common Feature of Size Datum Features are bores, cylinders, slots, or tab...
byDrPArivalaganASSTPRO
 
feature selection slides share and types of features selection
byQareenasadiq
 
Feature Selection.pdf
byadarshbarnwal5
 
International Journal of Engineering Research and Development (IJERD)
byIJERD Editor
 
Optimization Technique for Feature Selection and Classification Using Support...
byIJTET Journal
 
Bu-Refresher course PRESENTATION NEW.pptx
bysrideviramaraj2
 
Network Based Intrusion Detection System using Filter Based Feature Selection...
byIRJET Journal
 
Study on Relavance Feature Selection Methods
byIRJET Journal
 
Iaetsd an efficient and large data base using subset selection algorithm
byIaetsd Iaetsd
 
International Journal of Engineering Research and Development (IJERD)
byIJERD Editor
 
IRJET- Survey of Feature Selection based on Ant Colony
byIRJET Journal
 
6811067.ppt6811067.ppt6811067.ppt6811067.ppt
bynagalakshmig4
 
The International Journal of Engineering and Science (The IJES)
bytheijes
 
A fast clustering based feature subset selection algorithm for high-dimension...
byIEEEFINALYEARPROJECTS
 
JAVA 2013 IEEE DATAMINING PROJECT A fast clustering based feature subset sele...
byIEEEGLOBALSOFTTECHNOLOGIES
 
Feature Selection Algorithm for Supervised and Semisupervised Clustering
byEditor IJCATR
 
A Survey and Comparative Study of Filter and Wrapper Feature Selection Techni...
bytheijes
 
SEO PROCESS
byMohan Balakrishna
 

More from Andrea Gigli

PDF
Recommendation Systems in banking and Financial Services
byAndrea Gigli
 
PDF
Introduction to recommender systems
byAndrea Gigli
 
PPTX
Using R for Building a Simple and Effective Dashboard
byAndrea Gigli
 
PDF
Data Analytics per Manager
byAndrea Gigli
 
PDF
Impact of Valuation Adjustments (CVA, DVA, FVA, KVA) on Bank's Processes - An...
byAndrea Gigli
 
PPTX
From real to risk neutral probability measure for pricing and managing cva
byAndrea Gigli
 
PDF
Reasons behind XVAs
byAndrea Gigli
 
PPTX
A Data Scientist Job Map Visualization Tool using Python, D3.js and MySQL
byAndrea Gigli
 
PPTX
Search Engine Query Suggestion Application
byAndrea Gigli
 
PDF
Electricity Derivatives
byAndrea Gigli
 
PDF
Comparing Machine Learning Algorithms in Text Mining
byAndrea Gigli
 
PDF
How organizations can become data-driven: three main rules
byAndrea Gigli
 
PDF
Equity Value for Startups.pdf
byAndrea Gigli
 
PPTX
Lean Methods for Business & Social Innovation
byAndrea Gigli
 
PPTX
Presentazione Startup Saturday Europe @ ParmaCamp2013
byAndrea Gigli
 
PPTX
Crawling Tripadvisor Attracion Reviews - Italiano
byAndrea Gigli
 
PPTX
Search Engine for World Recipes Expo 2015
byAndrea Gigli
 
PPTX
Startup Saturday Internet Festival 2014
byAndrea Gigli
 
PDF
Balance-sheet dynamics impact on FVA, MVA, KVA
byAndrea Gigli
 
PPTX
Mine the Wine by Andrea Gigli
byAndrea Gigli
 
Recommendation Systems in banking and Financial Services
byAndrea Gigli
 
Introduction to recommender systems
byAndrea Gigli
 
Using R for Building a Simple and Effective Dashboard
byAndrea Gigli
 
Data Analytics per Manager
byAndrea Gigli
 
Impact of Valuation Adjustments (CVA, DVA, FVA, KVA) on Bank's Processes - An...
byAndrea Gigli
 
From real to risk neutral probability measure for pricing and managing cva
byAndrea Gigli
 
Reasons behind XVAs
byAndrea Gigli
 
A Data Scientist Job Map Visualization Tool using Python, D3.js and MySQL
byAndrea Gigli
 
Search Engine Query Suggestion Application
byAndrea Gigli
 
Electricity Derivatives
byAndrea Gigli
 
Comparing Machine Learning Algorithms in Text Mining
byAndrea Gigli
 
How organizations can become data-driven: three main rules
byAndrea Gigli
 
Equity Value for Startups.pdf
byAndrea Gigli
 
Lean Methods for Business & Social Innovation
byAndrea Gigli
 
Presentazione Startup Saturday Europe @ ParmaCamp2013
byAndrea Gigli
 
Crawling Tripadvisor Attracion Reviews - Italiano
byAndrea Gigli
 
Search Engine for World Recipes Expo 2015
byAndrea Gigli
 
Startup Saturday Internet Festival 2014
byAndrea Gigli
 
Balance-sheet dynamics impact on FVA, MVA, KVA
byAndrea Gigli
 
Mine the Wine by Andrea Gigli
byAndrea Gigli
 

Recently uploaded

PPTX
PLATELET RICH PLASMA in regenerative med
byDr SMRUTI REKHA HOTA
 
PDF
Overview of Ethiopian Agriculture: Systems and Economic Impact.pdf
byinebaseifu
 
PPTX
MELA QUIZ 2026 | Silchar Medical College & Hospital | 11-01-2026
byUltimatewinner0342
 
PDF
1.The-Story-of-Indian-Farming ppt/7th part 2/by k sandeep swamy(MSc,BEd)/samy...
bySandeep Swamy
 
PDF
2.India-and-Her-Neighbours ppt.pdf/Social science Grade 7 part -2 By:K SANDE...
bySandeep Swamy
 
PPTX
ANTI-TUSSIVE CHAPTER NO.05 PHARMACOGNOSY
byGanu Gavade
 
PPTX
Overview of SEO optimiser in Odoo 19 Website
byCeline George
 
PPTX
Complete and Detailed Overview of Odoo 18 Contact
byCeline George
 
PPTX
DIGITAL TRANSFORMATION MODULE KEY POINTS
byLisa Harris
 
PPTX
what are the Talent pool in Odoo 19 Recruitment
byCeline George
 
PDF
Halogen-Derivatives.pdf/BY K SANDEEP SWAMY/FOR ONLINE CLASSES CONTACT 9491878325
bySandeep Swamy
 
PDF
Fidelity to Energy: A Critical Analysis of Baz Luhrmann’s Intersemiotic Trans...
byKruti Vyas
 
PPTX
Prepositions of Place : English Grammar Presentation
byPintoo Dhillon
 
PPTX
Blood, Blood Composition, Blood Groups, Disorders of Blood.pptx
byAshish Umale
 
PPTX
special senses-eye, ear, nose, tongue.pptx
byAshish Umale
 
PPTX
Allow Quantity Modification in Combo in Odoo 19 pos
byCeline George
 
PPTX
GW4 BioMed Interview Support Webinar 2026
byGW4BioMedMRCDTP
 
PPTX
History in your Hands Class 5 January 2026 online slides.pptx
byEilsONeill
 
PPTX
Regenerate invoice in odoo 19 Accounting
byCeline George
 
PPTX
How to add bank Account in Odoo 19
byCeline George
 
PLATELET RICH PLASMA in regenerative med
byDr SMRUTI REKHA HOTA
 
Overview of Ethiopian Agriculture: Systems and Economic Impact.pdf
byinebaseifu
 
MELA QUIZ 2026 | Silchar Medical College & Hospital | 11-01-2026
byUltimatewinner0342
 
1.The-Story-of-Indian-Farming ppt/7th part 2/by k sandeep swamy(MSc,BEd)/samy...
bySandeep Swamy
 
2.India-and-Her-Neighbours ppt.pdf/Social science Grade 7 part -2 By:K SANDE...
bySandeep Swamy
 
ANTI-TUSSIVE CHAPTER NO.05 PHARMACOGNOSY
byGanu Gavade
 
Overview of SEO optimiser in Odoo 19 Website
byCeline George
 
Complete and Detailed Overview of Odoo 18 Contact
byCeline George
 
DIGITAL TRANSFORMATION MODULE KEY POINTS
byLisa Harris
 
what are the Talent pool in Odoo 19 Recruitment
byCeline George
 
Halogen-Derivatives.pdf/BY K SANDEEP SWAMY/FOR ONLINE CLASSES CONTACT 9491878325
bySandeep Swamy
 
Fidelity to Energy: A Critical Analysis of Baz Luhrmann’s Intersemiotic Trans...
byKruti Vyas
 
Prepositions of Place : English Grammar Presentation
byPintoo Dhillon
 
Blood, Blood Composition, Blood Groups, Disorders of Blood.pptx
byAshish Umale
 
special senses-eye, ear, nose, tongue.pptx
byAshish Umale
 
Allow Quantity Modification in Combo in Odoo 19 pos
byCeline George
 
GW4 BioMed Interview Support Webinar 2026
byGW4BioMedMRCDTP
 
History in your Hands Class 5 January 2026 online slides.pptx
byEilsONeill
 
Regenerate invoice in odoo 19 Accounting
byCeline George
 
How to add bank Account in Odoo 19
byCeline George
 

Feature Selection for Document Ranking

  • 1.
    Feature Selection Algorithmsfor Learning to Rank Andrea Gigli Email Slides: http://www.slideshare.net/andrgig March-2016
  • 2.
    Outline  Machine Learningfor Ranking  Proposed Feature Selection Algorithms (FSA) and Feature Selection Protocol  Application to Public Available Web Search Data
  • 3.
    Outline  Machine Learningfor Ranking  Proposed Feature Selection Algorithms (FSA) and Feature Selection Protocol  Application to Public Available Web Search Data
  • 4.
    Information Retrieval andRanking Systems  Information Retrieval is the activity of providing information offers relevant to an information need from a collection of information resources.  Ranking consists in sorting the information offers according to some criterion, so that the "best" results appear early in the provided list.
  • 5.
    Information Retrieval andRanking Systems Ranking System Information Request (Query) Information Offer (Documents) Indexed Documents Information Request Processing (Top) Ranked Documents
  • 6.
     Compute numericscores on query/document pairs Cosine Similarity, BM25 score, LMIR probabilities…  Use Machine Learning to build a ranking model Learning to Rank (L2R) How to Rank 𝑨 𝑪 𝑩 G C A 𝑫 Information Offers (Documents) Ranked List Information Request (Query) 𝑬 𝑮 𝑭 𝑯
  • 7.
    … … ... ... Learning System Ranking System Indexed Documents ... Training Prediction How to Rankusing Supervised Learning ... ... 𝑑1,1 𝑑1,2 ℓ1,1 𝑑1,𝑁1 ℓ1,2 ℓ1,𝑁1 … … 𝑑M,1 𝑑M,2 ℓ 𝑀,1 𝑑M,𝑁 𝑀 ℓ 𝑀,2 ℓ 𝑀,𝑁2 𝑞1 𝑞 𝑀 𝑓(𝑞, 𝑑) 𝑞 𝑀+1 𝑓(𝑞 𝑀+1, 𝑑 𝑁1 ) 𝑓(𝑞 𝑀+1, 𝑑 𝑁 𝑀 ) 𝑞𝑖: i-th query 𝑑𝑖,𝑗: j-th document associated to the i-th query ℓ𝑖,𝑗: observed score of the j-th document associated to the i-th query 𝑓(𝒒, 𝒐): scoring function
  • 8.
    Machine Learning forRanking Documents: Application Fields
  • 9.
    Machine Learning forRanking Documents: Business Cases
  • 10.
    Outline  Machine Learningfor Ranking  Proposed Feature Selection Algorithms (FSA) and Feature Selection Protocol  Application to Public Available Web Search Data
  • 11.
    Query & InformationOffer Features 𝑑𝑖,1 𝑑𝑖,2 𝑑𝑖,𝑁 𝑖𝑞𝑖 … …ℓ𝑖,1 ℓ𝑖,2 ℓ𝑖,𝑁 𝑖 𝑥𝑖,1 (1) 𝑥𝑖,1 (2) 𝑥𝑖,1 (3) ⋮ 𝑥𝑖,1 (𝐹) 𝑥𝑖,2 (1) 𝑥𝑖,2 (2) 𝑥𝑖,2 (3) ⋮ 𝑥𝑖,2 (𝐹) 𝑥𝑖,𝑁 𝑖 (1) 𝑥𝑖,𝑁 𝑖 (2) 𝑥𝑖,𝑁 𝑖 (3) ⋮ 𝑥𝑖,𝑁 𝑖 (𝐹) … Documents Query/Documents LabelsQuery  𝑓 𝒒, 𝒐 → 𝑓(𝒙)  F is of the order of hundreds, thousands
  • 12.
    Which features Case Featureexamples Web Search Query-URL matching features: number of occurrences of query terms in the document, BM25, N-gram BM25,Tf-Idf,… Importance of Url: PageRank , Number of in-links, Number of clicks, Browse Rank, Spam Score, Page Quality Score………….. Online Advertisement User features: last page visited, time from the last visit, last advertisement clicked, products queried… Product features: product description, product category, price… User-product matching feature: tf-idf, expected rating,… Page-Product matching feature: topic, category, tf-idf, … Collaborative Filtering User features: age, gender, consumption history, … Product characteristics: category, price, description, … Context - Product matching: tag-matching, tf-idf, … … …
  • 13.
    How to selectfeatures in L2R  The main goal of any feature selection process is to select a subset of n elements from a set of N measurement, with n<N, without significantly degrading the performance of the system  The search for the optimal subset require to search among 2N possible subsets
  • 14.
    How to selectfeatures in L2R 0 1,000,000 2,000,000 3,000,000 4,000,000 5,000,000 6,000,000 7,000,000 8,000,000 9,000,000 0 5 10 15 20 25 Number of possible feature subsets Number of Features A suboptimal criteria is needed
  • 15.
    Proposed Protocol forComparing Feature Selection Algorithms Measure the Relevance of each Feature Measure the Similarity of each pair of features Select a Feature Subset using a Feature Selector Train the L2R Model Measure the L2R Model Performance on theTest Set Compare Feature Selection Algorithms Repeat for different Subset Size 1 2 3 4 5 6 Repeat from 3 for every Feature Selection Algorithm
  • 16.
    Competing Algorithms forfeature selection We developed the following algorithms  Naïve Greedy searchAlgorithm for feature Selection (NGAS)  Naïve Greedy searchAlgorithm for feature Selection - Extended (NGAS-E)  Hierarchical Clustering search Algorithm for feature Selection (HCAS)
  • 17.
    Competing Algorithms forfeature selection We developed the following algorithms  Naïve Greedy searchAlgorithm for feature Selection (NGAS)  Naïve Greedy searchAlgorithm for feature Selection - Extended (NGAS-E)  Hierarchical Clustering search Algorithm for feature Selection (HCAS)
  • 18.
    Competing Algorithm forfeature selection #1: NGAS The undirect graph is built and the set S of selected features is initialized.
  • 19.
    Competing Algorithm forfeature selection #1: NGAS Assuming node 1 has the highest relevance, add it to S.
  • 20.
    Competing Algorithm forfeature selection #1: NGAS Select the node with the lowest similarity to Node 1, say Node 7, and the one with the highest similarity to Node 7, say Node 5.
  • 21.
    Competing Algorithm forfeature selection #1: NGAS Remove Node 1. Node 5 is the one with the highest relevance between 5 and 7, add it to S.
  • 22.
    Competing Algorithm forfeature selection #1: NGAS Select the node with the lowest similarity to Node 5, say Node 2, and the one with the highest similarity to Node 2, say Node 3.
  • 23.
    Competing Algorithm forfeature selection #1: NGAS Remove Node 5. Assuming Node 2 is the one with highest relevance between 2 and 3, add it to S.
  • 24.
    Competing Algorithm forfeature selection #1: NGAS Select the node with the lowest similarity to Node 2, say Node 4, and the one with the highest similarity to Node 4, say Node 8.
  • 25.
    Competing Algorithm forfeature selection #1: NGAS Remove Node 2. Assuming Node 4 is the one with highest relevance between 4 and 8, add it to S.
  • 26.
    Competing Algorithm forfeature selection #1: NGAS Select the node with the lowest similarity to Node 4, say Node 6, and the one with the highest similarity to Node 6, say Node 7.
  • 27.
    Competing Algorithm forfeature selection #1: NGAS Remove Node 4. Assuming Node 6 is the one with highest relevance between 6 and 7, add it to S.
  • 28.
    Competing Algorithm forfeature selection #1: NGAS Select the node with the lowest similarity to Node 6, say Node 3, and the one with the highest similarity to Node 3, say Node 8.
  • 29.
    Competing Algorithm forfeature selection #1: NGAS Remove Node 6. Assuming Node 3 is the one with highest relevance between 3 and 8, add it to S.
  • 30.
    Competing Algorithm forfeature selection #1: NGAS Select the node with the lowest similarity to Node 3, say Node 8, and the one with the highest similarity to Node 8, say Node 7.
  • 31.
    Competing Algorithm forfeature selection #1: NGAS Remove Node 3. Assuming Node 8 is the one with highest relevance between 8 and 7, add it to S.
  • 32.
    Competing Algorithm forfeature selection #1: NGAS Add the last node, 7, to S.
  • 33.
    We developed thefollowing algorithms  Naïve Greedy searchAlgorithm for feature Selection (NGAS)  Naïve Greedy searchAlgorithm for feature Selection - Extended (NGAS-E)  Hierarchical Clustering search Algorithm for feature Selection (HCAS) Competing Algorithms for feature selection
  • 34.
    Competing Algorithm forfeature selection #2: NGAS-E (p=50%) The undirect graph is built and the set S of selected features is initialized.
  • 35.
    Competing Algorithm forfeature selection #2: NGAS-E (p=50%) Assuming node 1 has the highest relevance, add it to S.
  • 36.
    Competing Algorithm forfeature selection #2: NGAS-E (p=50%) Select 7 ∗ 50% nodes less similar to 1.
  • 37.
    Competing Algorithm forfeature selection #2: NGAS-E (p=50%) Cancel Node 1 from the graph. Among the selected nodes, add the one with highest relevance (say node 5) to S.
  • 38.
    Competing Algorithm forfeature selection #2: NGAS-E (p=50%) Select ⌈6*50% ⌉ nodes less similar to node 5.
  • 39.
    Competing Algorithm forfeature selection #2: NGAS-E (p=50%) Cancel Node 5 from the graph. Among the selected nodes, add the one with highest relevance (say Node 3) to S.
  • 40.
    Competing Algorithm forfeature selection #2: NGAS-E (p=50%) Select ⌈5*50% ⌉ nodes less similar to node 3.
  • 41.
    Competing Algorithm forfeature selection #2: NGAS-E (p=50%) Cancel node 3 from the graph. Among the selected nodes, add the one with highest relevance (say node 4) to S.
  • 42.
    Competing Algorithm forfeature selection #2: NGAS-E (p=50%) Select ⌈4*50% ⌉ nodes less similar to node 4.
  • 43.
    Competing Algorithm forfeature selection #2: NGAS-E (p=50%) Cancel node 4 from the graph. Among the selected nodes, add the one with highest relevance (say node 6) to S.
  • 44.
    Competing Algorithm forfeature selection #2: NGAS-E (p=50%) Select ⌈3*50% ⌉ nodes less similar to node 6.
  • 45.
    Competing Algorithm forfeature selection #2: NGAS-E (p=50%) Cancel node 6 from the graph. Among the selected nodes, add the one with highest relevance (say node 2) to S.
  • 46.
    Competing Algorithm forfeature selection #2: NGAS-E (p=50%) Select ⌈2*50% ⌉nodes less similar to node 2.
  • 47.
    Competing Algorithm forfeature selection #2: NGAS-E (p=50%) Node 2 is cancelled from the graph and node 8 is added to S.
  • 48.
    Competing Algorithm forfeature selection #2: NGAS-E (p=50%) Node 8 is cancelled from the graph and the last node, 7, is added to S.
  • 49.
    Competing Algorithm forfeature selection #2: NGAS-E (p=50%) Node 8 is cancelled from the graph and the last node, 7, is added to S.
  • 50.
    We developed thefollowing algorithms  Naïve Greedy searchAlgorithm for feature Selection (NGAS)  Naïve Greedy searchAlgorithm for feature Selection - Extended (NGAS-E)  Hierarchical Clustering search Algorithm for feature Selection (HCAS) Competing Algorithms for feature selection
  • 51.
    Competing Algorithm forfeature selection #3: HCAS 23 11 5 3
  • 52.
    Outline  Machine Learningfor Ranking  Proposed Feature Selection Algorithms (FSA) and Feature Selection Protocol  Application to Public Available Web Search Data
  • 53.
    Application to WebSearch Engine Data  Bing Data http://research.microsoft.com/en-us/projects/mslr/  Yahoo! Data http://webscope.sandbox.yahoo.com Train Validation Test #queries 19,944 2,994 6,983 #urls 473,134 71,083 165,660 # features 519 Train Validation Test #queries 18,919 6,306 6,306 #urls 723,412 235,259 241,521 # features 136
  • 54.
    Proposed Protocol forComparing Feature Selection Algorithms Measure the Relevance of each Feature Measure the Similarity of each pair of features Select a Feature Subset using a Feature Selector Train the L2R Model Measure the L2R Model Performance on theTest Set Compare Feature Selection Algorithms Repeat for different Subset Size 1 2 3 4 5 6 Repeat from 3 for every Feature Selection Algorithm
  • 55.
    Learning to RankAlgorithms: a timeline of major contributions LambdaMART LambdaRank CRR IntervalRank GBlend NDCG Boost BayesRank BoltzRank MPBoost SortNet SSRankBoost RR SoftRank PermuRank ListMLE SVMmap RankRLS RankGP RankCosine QBRank McRank ListNet GBRank AdaRank IR-SVM RankNet RankBoost Pranking RankSVM 2000 2002 2003 2005 2006 2007 FRank 2008 2009 2010 Pointwise Pairwise Listwise
  • 56.
    Multiple Additive Regression Trees LambdaMART Model forLtR Lambda function  Ensemble method:Tree Boosting  Loss function not differentiable  Sorting characteristic  Speed
  • 57.
    Proposed Protocol forComparing Feature Selection Algorithms Measure the Relevance of each Feature Measure the Similarity of each pair of features Select a Feature Subset using a Feature Selector Train the L2R Model Measure the L2R Model Performance on theTest Set Compare Feature Selection Algorithms Repeat for different Subset Size 1 2 3 4 5 6 Repeat from 3 for every Feature Selection Algorithm
  • 58.
    Feature Relevance  Therelevance of a document is measured with a categorical variable (0,1,2,3,4)  we need to use metrics good at measuring «dependence» between discrete/continuous feature variables and a categorical label variable.  In the following we use  Normalized Mutual Information (NMI):  Spearman coefficient (S)  Kendall’s tau (K)  Average GroupVariance (AGV)  OneVariable NDCG@10 (1VNDCG)
  • 59.
    Feature Relevance viaNormalized Mutual Information  Mutual Information (MI) measures how much, on average, the realization of a random variable X tells us about the realization of the random variableY, or how much the entropy ofY, H(Y), is reduced knowing about the realization of X 𝑀𝐼 𝑋, 𝑌 = 𝐻 𝑋 − 𝐻 𝑋 𝑌 = 𝐻 𝑋 + 𝐻 𝑌 − 𝐻 𝑋, 𝑌 The normalizad version is 𝑁𝑀𝐼 𝑋, 𝑌 = 𝑀𝐼(𝑋, 𝑌) 𝐻(𝑋) 𝐻(𝑌)
  • 60.
    Feature Relevance viaSpearman’s coefficient  Spearman’s rank correlation coefficient is a non-parametric measure of statistical dependence between two random variables. It is given by 𝜌 = 1 − 6 𝑑𝑖 2 𝑛(𝑛2 − 1) where n is the sample size and 𝑑𝑖 = 𝑟𝑎𝑛𝑘 𝑥𝑖 − 𝑟𝑎𝑛𝑘 𝑦𝑖
  • 61.
    Feature Relevance viaKendall’s tau  Kendall’sTau is a measure of association defined on two ranking lists of length n. It is defined as τ = 𝑛 𝑐 − 𝑛 𝑑 𝑛(𝑛 − 1) 2 − 𝑛1 𝑛(𝑛 − 1) 2 − 𝑛2 where 𝑛 𝑐 denotes the number of concordant pairs between the two lists, 𝑛 𝑑 denotes the number of discordant pairs, 𝑛1 = 𝑡𝑖(𝑡𝑖 − 1)/2, 𝑛2 = 𝑢𝑗(𝑢𝑗 − 1)/2, 𝑡𝑖 is the number of tied values in the i-th group of ties for the first list and 𝑢𝑗 is the number of tied values in the j-th group of ties for the second list.
  • 62.
    Feature Relevance viaAverage GroupVariance  Average GroupVariance measure the discrimination power of a feature.The intuitive justification is that a feature is useful if it is capable of discriminating a small portion of the ordered scale from the rest, and that features with a small variance are those which satisfy this property. 𝐴𝐺𝑉 = 1 − 𝑔=1 5 𝑛 𝑔 𝑥 𝑔 − 𝑥 2 𝑖 𝑥𝑖 − 𝑥 2 where 𝑛 𝑔be the size of group g, 𝑥 𝑔 the sample mean of feature 𝑥 in the g-th group and 𝑥 whole sample mean.
  • 63.
    Feature Relevance viasingle feature LambdaMART scoring  For each feature i we run LambdaMART and compute the 𝑁𝐷𝐶𝐺𝑖,𝑞@10 for each query q  The i-th feature relevance is measured averaging 𝑁𝐷𝐶𝐺𝑖,𝑞@10 over the whole query set 𝑁𝐷𝐶𝐺𝑖@10 = 1 𝑄 𝑞∈𝑄 𝑁𝐷𝐶𝐺𝑖,𝑞@10
  • 64.
     Precision atk: 𝑃𝑖@𝑘 = # 𝑟𝑒𝑙𝑒𝑣𝑎𝑛𝑡 𝑑𝑜𝑐𝑢𝑚𝑒𝑛𝑡𝑠 𝑖𝑛 𝑡𝑜𝑝 𝑘 𝑟𝑒𝑠𝑢𝑙𝑡𝑠 𝑘  Average precision: 1 𝐷 𝑘=1 𝐷 𝑃𝑖@𝑘 ∙ 𝕀 𝑑𝑜𝑐𝑢𝑚𝑒𝑛𝑡 𝑘 𝑖𝑠 𝑟𝑒𝑙𝑒𝑣𝑎𝑛𝑡 # 𝑟𝑒𝑙𝑒𝑣𝑎𝑛𝑡 𝑑𝑜𝑐𝑢𝑚𝑒𝑛𝑡𝑠  Discounted Cumulative Gain 𝐷𝐶𝐺𝑖 = 𝑗=1 𝑘 2 𝑟𝑒𝑙 𝑖,𝑗 − 1 𝑙𝑜𝑔2 1 + 𝑟𝑎𝑛𝑘𝑗 How to Measure Ranking Performance on query i
  • 65.
    How to MeasureRanking Performance: Normalized DCG Document Gain Cumulative Gain Document 1 31 31 Document 2 3 34 Document 3 7 41 Document 4 31 72 Discounted 31x1=31 31+3x0.63=32.9 32.9+7x0.5=36.4 36.4+31x0.4=48.8 Normalization: divide DCG by the ideal DCG Document Gain Cumulative Gain Document 1 31 31 Document 4 31 62 Document 3 7 69 Document 2 3 72 Discounted 31x1=31 31+31x0.63=50.53 50.53+7x0.5=54.03 54.03+3x0.4=57.07 Relevance Rating Gain Perfect 25-1=31 Excellent 24-1=15 Good 23-1=7 Fair 22-1=3 Bad 21-1=1
  • 66.
  • 67.
  • 68.
    Choosing the RelevanceMeasure (1/2) FSA performance is measured using the Average NDCG@10 obtaind from LambdaMART on the test set. NDCG@10 on Yahoo Test Set Feature Subset Dimension 5% 10% 20% 30% 40% 50% 75% 100% NMI 0.73398 0.75952 0.76241 0.7678 0.76912 0.769 0.77015 0.76935 AVG 0.7524 0.7548 0.76168 0.76493 0.76498 0.76717 0.76971 0.76935 S 0.74963 0.75396 0.76099 0.76398 0.7649 0.76753 0.77002 0.76935 K 0.75225 0.75291 0.76145 0.76304 0.7648 0.76673 0.76972 0.76935 1VNDCG 0.75246 0.75768 0.76452 0.76672 0.76823 0.77008 0.77027 0.76935 NDCG@10 on Bing Test Set Feature Subset Dimension 5% 10% 20% 30% 40% 50% 75% 100% NMI 0.38927 0.3978 0.41347 0.41539 0.44785 0.44966 0.45083 0.46336 AVG 0.32682 0.33168 0.36043 0.36976 0.37383 0.37612 0.43444 0.46336 S 0.32969 0.3346 0.3428 0.34592 0.36711 0.42475 0.42809 0.46336 K 0.32917 0.3346 0.34356 0.42124 0.42071 0.4245 0.42706 0.46336 1VNDCG 0.41633 0.42571 0.42413 0.42601 0.42757 0.43795 0.46222 0.46336
  • 69.
  • 70.
    Proposed Protocol forComparing Feature Selection Algorithms Measure the Relevance of each Feature Measure the Similarity of each pair of features Select a Feature Subset using a Feature Selector Train the L2R Model Measure the Model Performance on theTest Set Compare Feature Selection Algorithms Repeat for different Subset Size 1 2 3 4 5 6 Repeat from 3 for every Feature Selection Algorithm
  • 71.
    Feature Similarity  Weused Spearman’s Rank coefficient for measuring features similarity.  Spearman’s Rank is faster to be computed than NMI, Kendall’s tau and 1VNDCG.
  • 72.
    The FSA benchmark:Greedy Algorithm for feature Selection 1. Build a complete undirected graph 𝐺0, in which a) each node represent the i-th feature with weight 𝑤𝑖 and b) each edge has weigth 𝑒𝑖,𝑗 2. Let 𝑆0 = ∅ be the set of selected features at step 0. 3. For i=1, …, n a) Select the node with largest weight from 𝐺𝑖−1, suppose that it is the k- th node b) Punish all the nodes connected with the k-th node: 𝑤𝑗 ← 𝑤𝑗 −2*c*𝑒 𝑘,𝑗, 𝑗 ≠ 𝑘 c) Add the k-th node to 𝑆𝑖−1 d) Remove the k-th node from 𝐺𝑖−1 4. Return 𝑆 𝑛
  • 73.
    Train the L2R Model ProposedProtocol for Comparing Feature Selection Algorithms Measure the Relevance of each Feature Measure the Similarity of each pair of features Select a Feature Subset using a Feature Selector Compare Feature Selection Algorithms Repeat for different Subset Size 1 2 3 4 5 6 Repeat from 3 for every Feature Selection Algorithm Measure the L2R Model Performance on theTest Set
  • 74.
    Proposed Protocol forComparing Feature Selection Algorithms Measure the Relevance of each Feature Measure the Similarity of each pair of features Select a Feature Subset using a Feature Selector Train the L2R Model Measure the L2R Model Performance on theTest Set Compare Feature Selection Algorithms 1 2 3 4 5 6 Repeat from 3 for every Feature Selection AlgorithmRepeat for different Subset Size
  • 75.
    Proposed Protocol forComparing Feature Selection Algorithms Measure the Relevance of each Feature Measure the Similarity of each pair of features Select a Feature Subset using a Feature Selector Train the L2R Model Compare Feature Selection Algorithms Repeat for different Subset Size 1 2 3 4 5 6 Repeat from 3 for every Feature Selection Algorithm Measure the Model Performance on theTest Set
  • 76.
  • 77.
    SignificanceTest using RandomizationTest NDCG@10 onYahoo Test Set Feature Subset Dimension 5% 10% 20% 30% 40% 50% 75% 100% NGAS 0.7430▼ 0.7601 0.7672 0.7717 0.7724 0.7759 0.7766 0.7753 NGAS-E, p = 0.8 0.7655 0.7666 0.7723 0.7742 0.7751 0.7759 0.776 0.7753 HCAS, "single" 0.7350▼ 0.7635 0.7666 0.7738 0.7742 0.7754 0.7756 0.7753 HCAS, "ward" 0.7570▼ 0.7626 0.7704 0.7743 0.7755 0.7763 0.7757 0.7753 GAS, c = 0.01 0.7628 0.7649 0.7671 0.773 0.7737 0.7737 0.7758 0.7753 NDCG@10 on Bing Test Set Feature Subset Dimension 5% 10% 20% 30% 40% 50% 75% 100% NGAS 0.4011▼ 0.4459 0.471 0.4739▼ 0.4813 0.4837 0.4831 0.4863 NGAS-E, p = 0.05 0.4376▲ 0.4528 0.4577▼ 0.4825 0.4834 0.4845 0.4867 0.4863 HCAS, "single" 0.4423▲ 0.4643▲ 0.4870▲ 0.4854 0.4848 0.4847 0.4853 0.4863 HCAS, "ward" 0.4289 0.4434▼ 0.4820 0.4879 0.4853 0.4837 0.4870 0.4863 GAS, c = 0.01 0.4294 0.4515 0.4758 0.4848 0.4863 0.4860 0.4868 0.4863
  • 78.
  • 79.
    Conclusions  We designed3 FSAs and we applied them to the Web Search Pages Ranking problem.  NGAS-E e HCAS have a performance equal or greater than the benchmark model.  HCAS and NGAS are very  The proposed FSAs can be implemented independently of the L2R model.  The proposed FSAs can be applied to other ML contexts, to Sorting problems and to Model Ensambling.
  • 80.