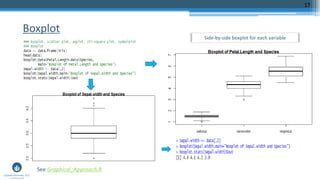
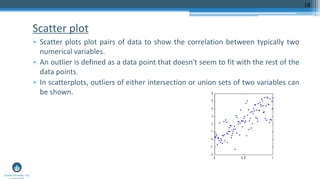
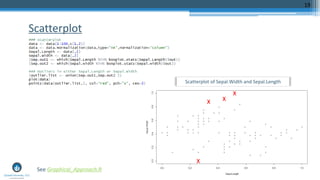
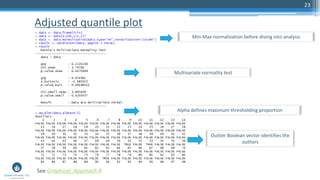
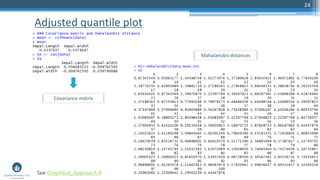
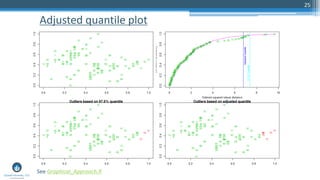
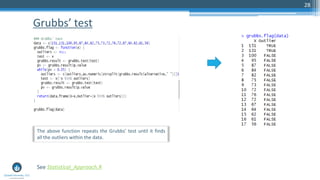
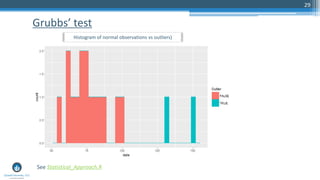
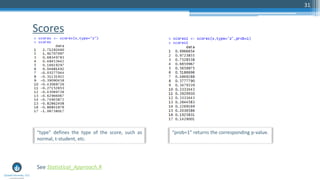
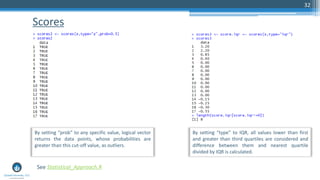
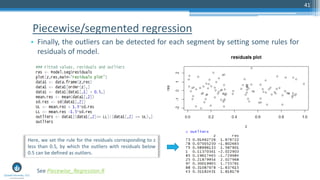
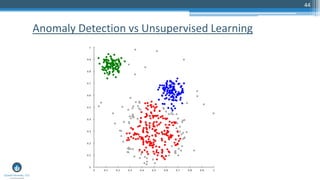
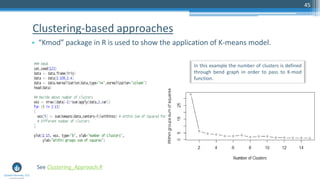
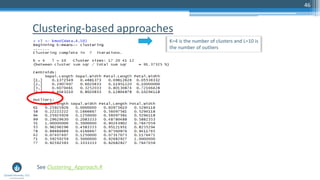
The document outlines a meetup focusing on anomaly detection techniques presented by Sri Krishnamurthy, founder of Quantuniversity LLC, detailing various methods including graphical, statistical, and machine learning approaches. It emphasizes the importance of identifying outliers in large datasets across fields such as finance and energy, along with key upcoming events and training programs from Quantuniversity. Additional resources and examples illustrate methodologies like boxplots, statistical testing, and clustering for detecting anomalies.

1. Location:
QuantUniversity Meetup
June 23rd 2016
Boston MA
Anomaly Detection
Techniques and Best Practices
2016 Copyright QuantUniversity LLC.
Presented By:
Sri Krishnamurthy, CFA, CAP
www.QuantUniversity.com
sri@quantuniversity.com

2. 2
Slides and Code available at:
http://www.analyticscertificate.com/Anomaly/

3. - Analytics Advisory services
- Custom training programs
- Architecture assessments, advice and audits

4. • Founder of QuantUniversity LLC. and
www.analyticscertificate.com
• Advisory and Consultancy for Financial Analytics
• Prior Experience at MathWorks, Citigroup and
Endeca and 25+ financial services and energy
customers (Shell, Firstfuel Software etc.)
• Regular Columnist for the Wilmott Magazine
• Author of forthcoming book
“Financial Modeling: A case study approach”
published by Wiley
• Charted Financial Analyst and Certified Analytics
Professional
• Teaches Analytics in the Babson College MBA
program and at Northeastern University, Boston
Sri Krishnamurthy
Founder and CEO
4

5. 5
Quantitative Analytics and Big Data Analytics Onboarding
• Trained more than 500 students in
Quantitative methods, Data Science
and Big Data Technologies using
MATLAB, Python and R
• Launching the Analytics Certificate
Program later in Fall

6. (MATLAB version also available)

7. 7
• July
▫ 11th : QuantUniversity’s 2nd meetup
 Topic : Quantitative methods topic : TBD
▫ 18th and 19th : 2-day workshop on Anomaly Detection
 Registration and pricing details at www.analyticscertificate.com/Anomaly
• August
▫ 8th : QuantUniversity meetup
▫ 14-20th : ARPM in New York www.arpm.co
 QuantUniversity presenting on Model Risk on August 14th
▫ 18-21st : Big-data Bootcamp http://globalbigdataconference.com/68/boston/big-
data-bootcamp/event.html
Events of Interest

8. 8
• July
▫ Anomaly Detection Workshop
▫ ARPM-prep seminar – Date TBD
• August
▫ Model Evaluation : Metrics, Scaling and Best Practices
• September
▫ What’s missing ? Best practices in missing data analysis
QuantUniversity’s Summer workshop series

9. 9

10. What is anomaly detection?
• Anomalies or outliers are data points that appear to deviate
markedly from expected outputs.
• It is the process of finding patterns in data that don’t
conform to a prior expected behavior.
• Anomaly detection is being employed more increasingly in
the presence of big data that is captured by sensors(IOT),
social media platforms, huge networks, etc. including
energy systems, medical devices, banking, network
intrusion detection, etc.
10

11. 11
• Fraud Detection
• Stock market
• E-commerce
Examples

12. 12
1. Graphical approach
2. Statistical approach
3. Machine learning approach
Three methodologies to Anomaly Detection

13. 13
 Boxplot
 Scatter plot
 Adjusted quantile plot

14. Anomaly Detection Methods
• Most outlier detection methods generate an output
that are:
▫ Real-valued outlier scores: quantifies the tendency of a
data point being an outlier by assigning a score or
probability to it.
▫ Binary labels: result of using a threshold to convert
outlier scores to binary labels, inlier or outlier.
14

15. Graphical approaches
• Statistical tails are most commonly used for one dimensional
distributions, although the same concept can be applied to
multidimensional case.
• It is important to understand that all extreme values are outliers
but the reverse may not be true.
• For instance in one dimensional dataset of
{1,3,3,3,50,97,97,97,100}, observation 50 equals to mean and isn’t
considered as an extreme value, but since this observation is the
most isolated point, it should be considered as an outlier.
15

16. Box plot
• A standardized way of displaying the
variation of data based on the five
number summary, which includes
minimum, first quartile, median, third
quartile, and maximum.
• This plot does not make any assumptions
of the underlying statistical distribution.
• Any data not included between the
minimum and maximum are considered
as an outlier.
16

17. Boxplot
17
See Graphical_Approach.R
Side-by-side boxplot for each variable

18. Scatter plot
• Scatter plots plot pairs of data to show the correlation between typically two
numerical variables.
• An outlier is defined as a data point that doesn't seem to fit with the rest of the
data points.
• In scatterplots, outliers of either intersection or union sets of two variables can
be shown.
18

19. Scatterplot
19
See Graphical_Approach.R
Scatterplot of Sepal.Width and Sepal.Length

20. 20
• In statistics, a Q–Q plot is a probability plot, which is a graphical
method for comparing two probability distributions by plotting their
quantiles against each other.
• If the two distributions being compared are similar, the points in the
Q–Q plot will approximately lie on the line y = x.
Q-Q plot
Source: Wikipedia

21. Adjusted quantile plot
• This plot identifies possible multivariate outliers by calculating the Mahalanobis
distance of each point from the center of the data.
• Multi-dimensional Mahalanobis distance between vectors x and y in 𝑅 𝑛 can be
formulated as:
d(x,y) = x − y TS−1(x − y)
where x and y are random vectors of the same distribution with the covariance
matrix S.
• An outlier is defined as a point with a distance larger than some pre-
determined value.
21

22. Adjusted quantile plot
• Before applying this method and many other parametric
multivariate methods, first we need to check if the data is
multivariate normally distributed using different
multivariate normality tests, such as Royston, Mardia, Chi-
square, univariate plots, etc.
• In R, we use the “mvoutlier” package, which utilizes
graphical approaches as discussed above.
22

23. Adjusted quantile plot
23
Min-Max normalization before diving into analysis
Multivariate normality test
Outlier Boolean vector identifies the
outliers
Alpha defines maximum thresholding proportion
See Graphical_Approach.R

24. Adjusted quantile plot
24
See Graphical_Approach.R
Mahalanobis distances
Covariance matrix

25. Adjusted quantile plot
25
See Graphical_Approach.R

26. 26
 Hypothesis testing (Grubb’s test)
 Scores

27. Grubbs’ test
• Test for outliers for univariate data sets assumed to come from a normally
distributed population.
• Grubbs' test detects one outlier at a time. This outlier is expunged from the
dataset and the test is iterated until no outliers are detected.
• This test is defined for the following hypotheses:
H0: There are no outliers in the data set
H1: There is exactly one outlier in the data set
• The Grubbs' test statistic is defined as:
27

28. Grubbs’ test
28
See Statistical_Approach.R
The above function repeats the Grubbs’ test until it finds
all the outliers within the data.

29. Grubbs’ test
29
See Statistical_Approach.R
Histogram of normal observations vs outliers)

30. Scores
• Scores quantifies the tendency of a data point being an outlier by assigning it a
score or probability.
• The most commonly used scores are:
▫ Normal score:
𝑥 𝑖 −𝑀𝑒𝑎𝑛
𝑠𝑡𝑎𝑛𝑑𝑎𝑟𝑑 𝑑𝑒𝑣𝑖𝑎𝑡𝑖𝑜𝑛
▫ T-student score:
(𝑧−𝑠𝑞𝑟𝑡 𝑛−2 )
𝑠𝑞𝑟𝑡(𝑧−1−𝑡2)
▫ Chi-square score:
𝑥 𝑖 −𝑀𝑒𝑎𝑛
𝑠𝑑
2
▫ IQR score: 𝑄3-𝑄1
• By using “score” function in R, p-values can be returned instead of scores.
30

31. Scores
31
See Statistical_Approach.R
“type” defines the type of the score, such as
normal, t-student, etc.
“prob=1” returns the corresponding p-value.

32. Scores
32
See Statistical_Approach.R
By setting “prob” to any specific value, logical vector
returns the data points, whose probabilities are
greater than this cut-off value, as outliers.
By setting “type” to IQR, all values lower than first
and greater than third quartiles are considered and
difference between them and nearest quartile
divided by IQR is calculated.

33. 33
• Anomaly Detection
▫ Seasonal Hybrid ESD (S-H-ESD) builds upon the Generalized ESD test for
detecting anomalies.
▫ Anomaly detection referring to point-in-time anomalous data points that
could be global or local. A local anomaly is one that occurs inside a seasonal
pattern; Could be +ve or –ve.
▫ More details here: https://github.com/twitter/AnomalyDetection
• Breakout Detection
▫ A breakout is characterized in this package by two steady states and an
intermediate transition period that could be sudden or gradual
▫ Uses the E-Divisive with Medians algorithm; Can detect one or multiple
breakouts in a given time series and employs energy statistics to detect
divergence in mean. More details here:
(https://blog.twitter.com/2014/breakout-detection-in-the-wild )
Twitter packages
Ref: http://www.itl.nist.gov/div898/handbook/eda/section3/eda35h3.htm

34. 34
• Twitter-R-Anomaly Detection tutorial.ipyb
Demo

35. 35
 Linear regression
 Piecewise/ segmented regression
 Clustering-based approaches

36. Linear regression
• Linear regression investigates the linear relationships between variables and
predict one variable based on one or more other variables and it can be
formulated as:
𝑌 = 𝛽0 + ෍
𝑖=1
𝑝
𝛽𝑖 𝑋𝑖
where Y and 𝑋𝑖 are random variables, 𝛽𝑖 is regression coefficient and 𝛽0 is a
constant.
• In this model, ordinary least squares estimator is usually used to minimize the
difference between the dependent variable and independent variables.
36

37. Piecewise/segmented regression
• A method in regression analysis, in which the independent variable is
partitioned into intervals to allow multiple linear models to be fitted to data for
different ranges.
• This model can be applied when there are ‘breakpoints’ and clearly two
different linear relationships in the data with a sudden, sharp change in
directionality. Below is a simple segmented regression for data with two
breakpoints:
𝑌 = 𝐶0 + 𝜑1 𝑋 𝑋 < 𝑋1
𝑌 = 𝐶1 + 𝜑2 𝑋 𝑋 > 𝑋1
where Y is a predicted value, X is an independent variable, 𝐶0 and 𝐶1 are
constant values, 𝜑1 and 𝜑2 are regression coefficients, and 𝑋1 and 𝑋2 are
breakpoints.
37

38. 38
Anomaly detection vs Supervised learning

39. Piecewise/segmented regression
• For this example, we use “segmented” package in R to first illustrate piecewise
regression for two dimensional data set, which has a breakpoint around z=0.5.
39
See Piecewise_Regression.R
“pmax” is used for parallel maximization to
create different values for y.

40. Piecewise/segmented regression
• Then, we use linear regression to predict y values for each segment of z.
40
See Piecewise_Regression.R

41. Piecewise/segmented regression
• Finally, the outliers can be detected for each segment by setting some rules for
residuals of model.
41
See Piecewise_Regression.R
Here, we set the rule for the residuals corresponding to z
less than 0.5, by which the outliers with residuals below
0.5 can be defined as outliers.

42. Clustering-based approaches
• These methods are suitable for unsupervised anomaly detection.
• They aim to partition the data into meaningful groups (clusters) based on the
similarities and relationships between the groups found in the data.
• Each data point is assigned a degree of membership for each of the clusters.
• Anomalies are those data points that:
▫ Do not fit into any clusters.
▫ Belong to a particular cluster but are far away from the cluster centroid.
▫ Form small or sparse clusters.
42

43. Clustering-based approaches
• These methods partition the data into k clusters by assigning each data point to
its closest cluster centroid by minimizing the within-cluster sum of squares
(WSS), which is:
෍
𝑘=1
𝐾
෍
𝑖∈𝑆 𝑘
෍
𝑗=1
𝑃
(𝑥𝑖𝑗 − 𝜇 𝑘𝑗)2
where 𝑆 𝑘 is the set of observations in the kth cluster and 𝜇 𝑘𝑗 is the mean of jth
variable of the cluster center of the kth cluster.
• Then, they select the top n points that are the farthest away from their nearest
cluster centers as outliers.
43

44. 44
Anomaly Detection vs Unsupervised Learning

45. Clustering-based approaches
• “Kmod” package in R is used to show the application of K-means model.
45
In this example the number of clusters is defined
through bend graph in order to pass to K-mod
function.
See Clustering_Approach.R

46. Clustering-based approaches
46
See Clustering_Approach.R
K=4 is the number of clusters and L=10 is
the number of outliers

47. Clustering-based approaches
47
See Clustering_Approach.R
Scatter plots of normal and outlier data points

48. Summary
48
We have covered Anomaly detection
Introduction  Definition of anomaly detection and its importance in energy systems
 Different types of anomaly detection methods: Statistical, graphical and machine
learning methods
Graphical approach  Graphical methods consist of boxplot, scatterplot, adjusted quantile plot and symbol
plot to demonstrate outliers graphically
 The main assumption for applying graphical approaches is multivariate normality
 Mahalanobis distance methods is mainly used for calculating the distance of a point
from a center of multivariate distribution
Statistical approach  Statistical hypothesis testing includes of: Chi-square, Grubb’s test
 Statistical methods may use either scores or p-value as threshold to detect outliers
Machine learning approach  Both supervised and unsupervised learning methods can be used for outlier detection
 Piece wised or segmented regression can be used to identify outliers based on the
residuals for each segment
 In K-means clustering method outliers are defined as points which have doesn’t belong
to any cluster, are far away from the centroids of the cluster or shaping sparse clusters

49. (MATLAB version also available)
www.analyticscertificate.com

50. 50
Q&A
Slides, code and details about the Anomaly detection workshop
at: http://www.analyticscertificate.com/Anomaly/

51. Thank you!
Members &
Sri Krishnamurthy, CFA, CAP
Founder and CEO
QuantUniversity LLC.
srikrishnamurthy
www.QuantUniversity.com
Contact
Information, data and drawings embodied in this presentation are strictly a property of QuantUniversity LLC. and shall not be
distributed or used in any other publication without the prior written consent of QuantUniversity LLC.
51