Downloaded 111 times
Uploaded byQuantUniversity
Machine learning meetup
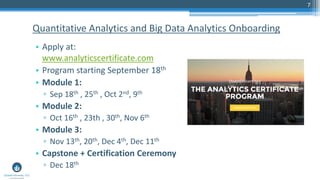
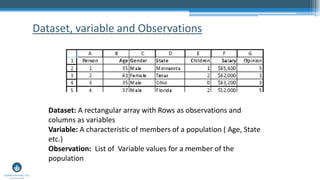
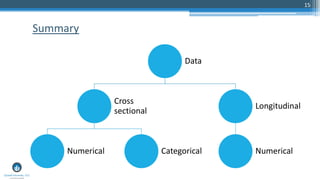
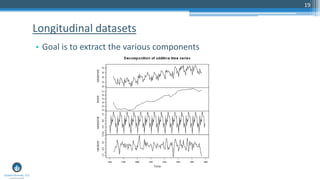
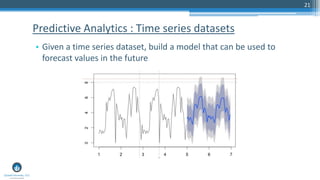
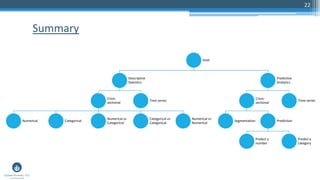
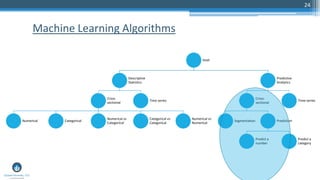
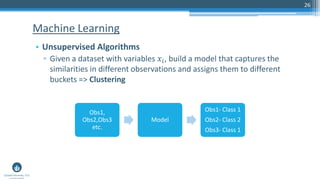
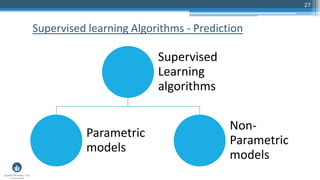
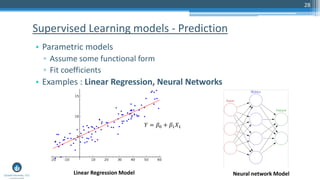
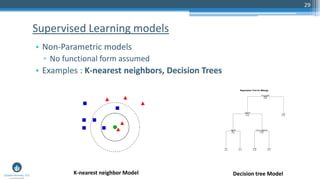
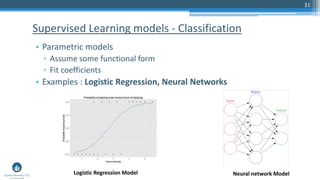
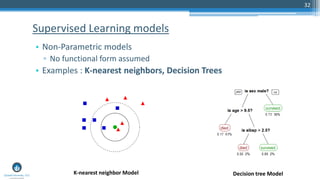
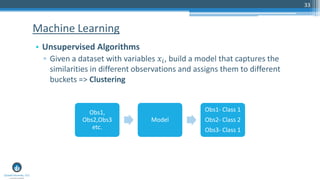
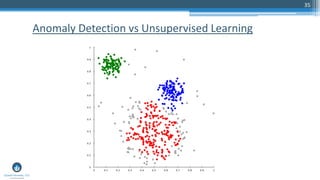
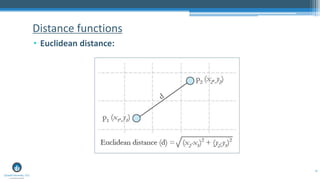
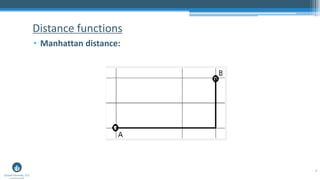
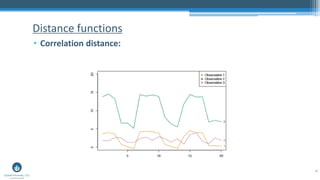
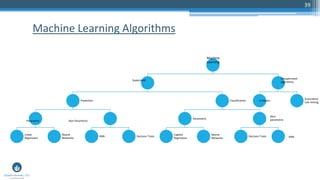
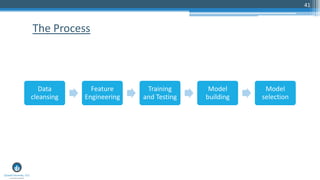
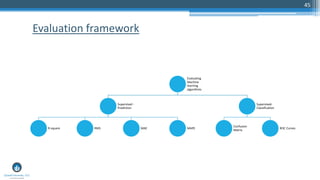
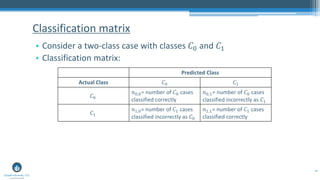
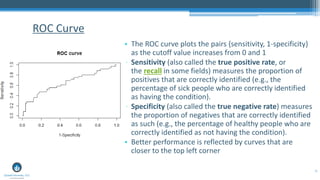
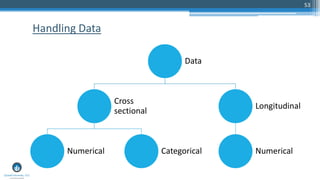
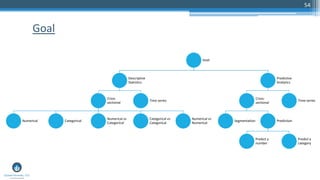
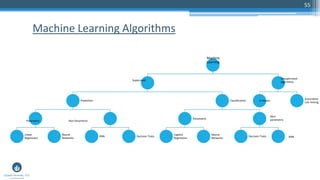
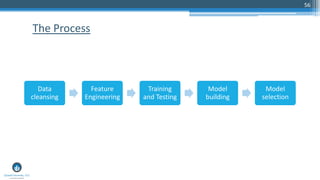
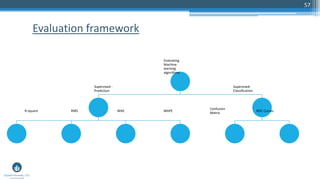
The document outlines a presentation by Sri Krishnamurthy at a QuantUniversity meetup in Boston on machine learning basics, focusing on analytics education and upcoming training programs. It covers essential topics such as data types, descriptive and predictive analytics, machine learning algorithms, and evaluation methods. Additionally, it promotes various workshops and courses related to analytics, starting in September 2016.
More Related Content
Similar to Machine learning meetup
Machine learning meetup
- 1. Location: QuantUniversity Meetup August 24th2016 Boston MA Machine Learning: An intuitive foundation 2016 Copyright QuantUniversity LLC. Presented By: Sri Krishnamurthy, CFA, CAP www.QuantUniversity.com sri@quantuniversity.com
- 2. 2 Slides and Codewill be available at: http://www.analyticscertificate.com
- 3. - Analytics Advisoryservices - Custom training programs - Architecture assessments, advice and audits
- 4. ⢠Founder ofQuantUniversity LLC. and www.analyticscertificate.com ⢠Advisory and Consultancy for Financial Analytics ⢠Prior Experience at MathWorks, Citigroup and Endeca and 25+ financial services and energy customers. ⢠Regular Columnist for the Wilmott Magazine ⢠Author of forthcoming book âFinancial Modeling: A case study approachâ published by Wiley ⢠Charted Financial Analyst and Certified Analytics Professional ⢠Teaches Analytics in the Babson College MBA program and at Northeastern University, Boston Sri Krishnamurthy Founder and CEO 4
- 5. 5 Quantitative Analytics andBig Data Analytics Onboarding ⢠Trained more than 500 students in Quantitative methods, Data Science and Big Data Technologies using MATLAB, Python and R ⢠Launching the Analytics Certificate Program in September
- 7. 7 Quantitative Analytics andBig Data Analytics Onboarding ⢠Apply at: www.analyticscertificate.com ⢠Program starting September 18th ⢠Module 1: ⍠Sep 18th , 25th , Oct 2nd, 9th ⢠Module 2: ⍠Oct 16th , 23th , 30th, Nov 6th ⢠Module 3: ⍠Nov 13th, 20th, Dec 4th, Dec 11th ⢠Capstone + Certification Ceremony ⍠Dec 18th
- 8. 8 ⢠September ⍠11th,12th : Spark Workshop, Boston ď www.analyticscertificate.com/SparkWorkshop ď Sponsored by IBM ⍠19th, 20th : Anomaly Detection Workshop, New York ď www.analyticscertificate.com/AnomalyNYC ď Sponsored by Microsoft Events of Interest
- 9.
- 10. Agenda 1. Data 2. Goals 3.Machine learning algorithms 4. Process 5. Performance Evaluation
- 11.
- 12. Dataset, variable andObservations Dataset: A rectangular array with Rows as observations and columns as variables Variable: A characteristic of members of a population ( Age, State etc.) Observation: List of Variable values for a member of the population
- 13. Variables ď A variablecould be: ďCategorical ď Yes/No flags ď AAA,BB ratings for bonds ďNumerical ď 35 mpg ď $170K salary
- 14. Datasets ⢠Longitudinal ⍠Observationsare dependent ⍠Temporal-continuity is required ⢠Cross-sectional ⍠Observations are independent
- 15.
- 16.
- 17. 17 ⢠Descriptive Statistics âŤGoal is to describe the data at hand ⍠Backward looking ⍠Statistical techniques employed here ⢠Predictive Analytics ⍠Goal is to use historical data to build a model for prediction ⍠Forward looking ⍠Machine learning techniques employed here Goal
- 18. 18 ⢠How doyou summarize numerical variables ? ⢠How do you summarize categorical variables ? ⢠How do you describe variability in numerical variables ? ⢠How do you summarize relationships between categorical and numerical variables ? ⢠How do you summarize relationships between 2 numerical variables? Descriptive Statistics â Cross sectional datasets See Data Analysis Taxonomy.xlsx
- 19. 19 ⢠Goal isto extract the various components Longitudinal datasets
- 20. 20 ⢠Given adataset, build a model that captures the similarities in different observations and assigns them to different buckets. ⢠Given a set of variables, predict the value of another variable in a given data set ⍠Predict Salaries given work experience, education etc. ⍠Predict whether a loan would be approved given fico score, current loans, employment status etc. Predictive Analytics : Cross sectional datasets
- 21. 21 ⢠Given atime series dataset, build a model that can be used to forecast values in the future Predictive Analytics : Time series datasets
- 22. 22 Goal Descriptive Statistics Cross sectional Numerical Categorical Numerical vs Categorical Categoricalvs Categorical Numerical vs Numerical Time series Predictive Analytics Cross- sectional Segmentation Prediction Predict a number Predict a category Time-series Summary
- 23.
- 24. 24 Machine Learning Algorithms Goal Descriptive Statistics Cross sectional NumericalCategorical Numerical vs Categorical Categorical vs Categorical Numerical vs Numerical Time series Predictive Analytics Cross- sectional Segmentation Prediction Predict a number Predict a category Time-series
- 25. 25 ⢠Supervised Algorithms âŤGiven a set of variables đĽđ, predict the value of another variable đŚ in a given data set such that ⍠If y is numeric => Prediction ⍠If y is categorical => Classification Machine Learning x1,x2,x3⌠Model F(X) y
- 26. 26 ⢠Unsupervised Algorithms âŤGiven a dataset with variables đĽđ, build a model that captures the similarities in different observations and assigns them to different buckets => Clustering Machine Learning Obs1, Obs2,Obs3 etc. Model Obs1- Class 1 Obs2- Class 2 Obs3- Class 1
- 27.
- 28. 28 ⢠Parametric models âŤAssume some functional form ⍠Fit coefficients ⢠Examples : Linear Regression, Neural Networks Supervised Learning models - Prediction đ = đ˝0 + đ˝1 đ1 Linear Regression Model Neural network Model
- 29. 29 ⢠Non-Parametric models âŤNo functional form assumed ⢠Examples : K-nearest neighbors, Decision Trees Supervised Learning models K-nearest neighbor Model Decision tree Model
- 30. ⢠Given estimatesáđ˝0, áđ˝1, ⌠, áđ˝ đWe can make predictions using the formula ŕˇđŚ = áđ˝0 + áđ˝1 đĽ1 + áđ˝2 đĽ2 + ⯠+ áđ˝ đ đĽ đ ⢠The parameters are estimated using the least squares approach to minimize the sum of squared errors đ đđ = ࡠđ=1 đ (đŚđ â ŕˇđŚđ)2 Multiple linear regression 30
- 31. 31 ⢠Parametric models âŤAssume some functional form ⍠Fit coefficients ⢠Examples : Logistic Regression, Neural Networks Supervised Learning models - Classification Logistic Regression Model Neural network Model
- 32. 32 ⢠Non-Parametric models âŤNo functional form assumed ⢠Examples : K-nearest neighbors, Decision Trees Supervised Learning models K-nearest neighbor Model Decision tree Model
- 33. 33 ⢠Unsupervised Algorithms âŤGiven a dataset with variables đĽđ, build a model that captures the similarities in different observations and assigns them to different buckets => Clustering Machine Learning Obs1, Obs2,Obs3 etc. Model Obs1- Class 1 Obs2- Class 2 Obs3- Class 1
- 34. K-means clustering ⢠Thesemethods partition the data into k clusters by assigning each data point to its closest cluster centroid by minimizing the within-cluster sum of squares (WSS), which is: ࡠđ=1 đž ࡠđâđ đ ࡠđ=1 đ (đĽđđ â đ đđ)2 where đ đ is the set of observations in the kth cluster and đ đđ is the mean of jth variable of the cluster center of the kth cluster. ⢠Then, they select the top n points that are the farthest away from their nearest cluster centers as outliers. 34
- 35. 35 Anomaly Detection vsUnsupervised Learning
- 36. 36 Distance functions ⢠Euclideandistance:
- 37. 37 Distance functions ⢠Manhattandistance: D =|đđ´- đ đľ|+ |đđ´- đđľ|
- 38.
- 39. 39 Machine Learning Algorithms Machine Learning Supervised Prediction Parametric Linear Regression Neural Networks Non- parametric KNNDecision Trees Classification Parametric Logistic Regression Neural Networks Non Parametric Decision Trees KNN Unsupervised algorithms K-means Associative rule mining
- 40.
- 41.
- 42. 42 ⢠What transformationsdo I need for the x and y variables ? ⢠Which are the best features to use? ⍠Dimension Reduction â PCA ⍠Best subset selection ď Forward selection ď Backward elimination ď Stepwise regression Feature Engineering
- 43.
- 44.
- 45. 45 Evaluating Machine learning algorithms Supervised - Prediction R-square RMSMAE MAPE Supervised- Classification Confusion Matrix ROC Curves Evaluation framework
- 46. 46 ⢠The predictionerror for record i is defined as the difference between its actual y value and its predicted y value đđ = đŚđ â ŕˇđŚđ ⢠đ 2 indicates how well data fits the statistical model đ 2 = 1 â Ďđ=1 đ (đŚđ â ŕˇđŚđ)2 Ďđ=1 đ (đŚđ â ŕ´¤đŚđ)2 Prediction Accuracy Measures
- 47. 47 ⢠Fit measuresin classical regression modeling: ⢠Adjusted đ 2 has been adjusted for the number of predictors. It increases only when the improve of model is more than one would expect to see by chance (p is the total number of explanatory variables) đ´đđđ˘đ đĄđđ đ 2 = 1 â ΤĎđ=1 đ (đŚđ â ŕˇđŚđ)2 (đ â đ â 1) Ďđ=1 đ đŚđ â ŕ´¤đŚđ 2 /(đ â 1) ⢠MAE or MAD (mean absolute error/deviation) gives the magnitude of the average absolute error đđ´đ¸ = 1 đ Ďđ=1 đ đđ Prediction Accuracy Measures
- 48. 48 ⍠MAPE (meanabsolute percentage error) gives a percentage score of how predictions deviate on average đđ´đđ¸ = 1 đ Ďđ=1 đ đđ/đŚđ Ă 100% ⢠RMSE (root-mean-squared error) is computed on the training and validation data đ đđđ¸ = 1/đ ࡠđ=1 đ đđ 2 Prediction Accuracy Measures
- 49. 49 ⢠Consider atwo-class case with classes đś0 and đś1 ⢠Classification matrix: Classification matrix Predicted Class Actual Class đś0 đś1 đś0 đ0,0= number of đś0 cases classified correctly đ0,1= number of đś0 cases classified incorrectly as đś1 đś1 đ1,0= number of đś1 cases classified incorrectly as đś0 đ1,1= number of đś1 cases classified correctly
- 50. 50 ⢠Estimated misclassificationrate (overall error rate) is a main accuracy measure đđđ = đ0,1 + đ1,0 đ0,0 + đ0,1 + đ1,0 + đ1,1 = đ0,1 + đ1,0 đ ⢠Overall accuracy: đ´đđđ˘đđđđŚ = 1 â đđđ = đ0,0 + đ1,1 đ Accuracy Measures
- 51. 51 ⢠The ROCcurve plots the pairs {sensitivity, 1-specificity} as the cutoff value increases from 0 and 1 ⢠Sensitivity (also called the true positive rate, or the recall in some fields) measures the proportion of positives that are correctly identified (e.g., the percentage of sick people who are correctly identified as having the condition). ⢠Specificity (also called the true negative rate) measures the proportion of negatives that are correctly identified as such (e.g., the percentage of healthy people who are correctly identified as not having the condition). ⢠Better performance is reflected by curves that are closer to the top left corner ROC Curve
- 52. Agenda 1. Data 2. Goals 3.Machine learning algorithms 4. Process 5. Performance Evaluation
- 53.
- 54. 54 Goal Descriptive Statistics Cross sectional Numerical Categorical Numerical vs Categorical Categoricalvs Categorical Numerical vs Numerical Time series Predictive Analytics Cross- sectional Segmentation Prediction Predict a number Predict a category Time-series Goal
- 55. 55 Machine Learning Algorithms Machine Learning Supervised Prediction Parametric Linear Regression Neural Networks Non- parametric KNNDecision Trees Classification Parametric Logistic Regression Neural Networks Non Parametric Decision Trees KNN Unsupervised algorithms K-means Associative rule mining
- 56.
- 57. 57 Evaluating Machine learning algorithms Supervised - Prediction R-square RMSMAE MAPE Supervised- Classification Confusion Matrix ROC Curves Evaluation framework
- 60.
- 61. 61 Q&A Slides, code anddetails about the Apache Spark Workshop at: http://www.analyticscertificate.com/SparkWorkshop/
- 62. Thank you! Members &Sponsors! Sri Krishnamurthy, CFA, CAP Founder and CEO QuantUniversity LLC. srikrishnamurthy www.QuantUniversity.com Contact Information, data and drawings embodied in this presentation are strictly a property of QuantUniversity LLC. and shall not be distributed or used in any other publication without the prior written consent of QuantUniversity LLC. 62