The document discusses Rolle's Theorem and its implications, stating that if a function is continuous on a closed interval and differentiable on an open interval with equal values at the endpoints, there exists at least one point where the derivative is zero. It further explores Lagrange's Mean Value Theorem and Cauchy's Mean Value Theorem, providing statements and proofs for each, along with examples verifying these theorems using specific functions. The text serves as a comprehensive overview of key concepts in advanced calculus related to these theorems.

1. B.SC. - II (MATHEMATICS)
ADVANCED CALCULUS
ROLLE’S THEOREM
By Preeti Shrivastava

2. SYNOPSIS
 Rolle’s Theorem
 Rolle’s theorem’s Example
 Lagrange’s Mean Value Theorem (first mean value
theorem)
 Example of Lagrange’s mean value theorem
 Cauchy’s Mean Value Theorem(second mean value
theorem)
 Example of Cauchy’s mean value theorem

3. ROLLE’S
THEOREM

4. Statement:-
If f(x) is a function of the variable x such that :-
 f(x) is continuous in the closed interval [a,b].
 f(x) is differentiable for every point in the open
interval (a,b).
 f(a) = f(b), then there is at least one point c such that
f’(c) =0.

5. Proof:-
 We need to know Close Interval and Open Interval:
 Open Interval:- An open interval is an interval that
does not include its two mid- point .The open interval
{x:a<x<b} is denoted by (a,b).
 Close Interval:- A closed interval is an interval that
include all its limit point. A finite number a and b
then the interval {x:a<x<b} is denoted by [a,b].
 Case 1:- If f(x) is constant then,
f(x) = k (constant)
f(a) = k
f(b) = k

6.  so, f(a) = f(b) f(a) f(b)
since, f(x) =k a b
therefore f’(x) =0
and f’(c) =0
 Case 2:- If function f(x) will first increase and then decreases.
Then at some point C consequently f(x) will be maximum.
Then f(c-h) < f (c) and f(c+h) < f(c)
f(c-h) – f(c) < 0 and f(c+h) - f(c) < 0
Taking limit on both sides:



x
h
cfhcf

 )()(
0 0
)()(


h
cfhcf
and

7. Case 3:- - If function f(x) w ill first decrease and then
increases. Then at some point C consequently f(x)
w ill be minimum.
Then
 – > 0

Taking limits on both sides:-




8. Verify Rolle’s theorem in the interval
(2,4] for the
function 𝒇 𝒙 = 𝒙 𝟐
− 𝟔𝒙 + 𝟖
Solution:-
Given that ,
𝑓 𝑥 = 𝑥2
− 6𝑥 + 8
[a,b] =[2,4]
a =2, b=4.
By Rolle’s theorem
∵ 𝑓 𝑥 = 𝑥2
− 6𝑥 + 8
∴ 𝑓′
𝑥 = 2𝑥 − 6
𝑓’(𝑐) = 2𝑐 − 6

9. ∵ 𝑓’(𝑐) = 0
∴ 2𝑐 − 6 = 0
2𝑐 = 6
𝐶 = 3 ∈ [2,4]
Here a<c<b
Hence Rolle ’s Theorem is verified.

10. LAGRANGE’S
MEAN VALUE
THEOREM

11. Statement:-
If f(x) is a function of the variable x and :-
(1) f(x) is continuous in the closed interval [a,b].
(2) f(x) differentiable in the open interval (a,b), then there
exists at least one point c in the open interval (a,b) such
that
Proof:-
If f(x) is a function of the variable x.
Where A is constant to be determined such that
∵ f(x) is continuous in the closed interval [a,b).
∴ ∅(x)is also continuous in the closed interval [a,b].
Again, ∵ f(x) differentiable in the open interval (a,b).
∴ ∅(x) is also differentiable in the open interval (a,b).

12. Hence by the Rolle’s theorem,
Then there exist at least one point c such that ∅’ c = 0
…. III
From equation (I)
∅(x) = f(x) + A.x
∅(a) = f(a) + A.a ….. IV
∅(b) = f(b) + A.b …… V
From equation (II)
∅(𝑎) = ∅(𝑏)
𝑓(𝑎) + 𝐴. 𝑎 = 𝑓(𝑏) + 𝐴. 𝑥
𝐴. 𝑎 – 𝐴. 𝑏 = 𝑓(𝑏) – 𝑓(𝑎)
−𝐴(𝑏 − 𝑎) = 𝑓(𝑏) – 𝑓(𝑎)
−𝐴 =
𝑓 𝑏 −𝑓(𝑎)
𝑏−𝑎
… . . (𝑉𝐼)
Again, from equation (I)
∅(𝑥) = 𝑓(𝑥) + 𝐴𝑥
∅’(𝑥) = 𝑓’(𝑥) + 𝐴

13. …… VII
Example:-
Verify Lagrange’s mean value theorem for the function
in the interval [2,4].
Solution:-
It is given that

14. 𝑓’(𝑥) =
𝑥
𝑥2−4
… … (𝐼𝐼)
∵ 𝑓(𝑥) = 𝑥2 − 4
∴ 𝑓(𝑎) = 𝑓(2) = 22 − 4 = 0
𝐹(𝑏) = 𝑓(4) = 42 − 4 = 12
By Lagrange’s mean value theorem,
𝑓′
𝑐 =
𝑓 𝑏 − 𝑓(𝑎)
𝑏−𝑎
𝑐
𝑐2−4
=
12−0
4−2
𝑐
𝑐2−4
=
12
2

15.  Squaring on both side
bCa
C
C
C
CC
CC
C
C









462
6
6
488
41248
48124
4
12
4
2
2
22
22
2
2

Hence Lagrange’s Theorem is Verified.

16. CAUCHY’ MEAN
VALUE THEOREM

17. Statement:-
If two function f(x) and g(x) are:-
Continuous in the Closed Interval [a,b].
Differentiable in the Open Interval [a,b].
Then there is at least one point c such that:-
where a<c<b
 Proof:-
Now consider a function F(x) defined by:-
F(x)= f(x)+ A(x) ……….(I)
Where A is a constant to be determined
)()(
)()'(
ab
aFbF



 )('
)('
c
cF

18. such that :
F(a) = F(b) ……….(II)
Since f(x) are continuous in closed interval
[a,b].
So, F(x) is also continuous in closed interval
[a,b].
 Again,
f(x) are differentiable in Open interval
(a,b).
So, F(x) is also differentiable in the open
interval (a,b)
Then all condition of Rolle’s Theorem will be
satisfied .

19.  Hence by the Rolle’s Theorem there at least
one Point C in
 open interval (a,b) such that F’(c) =0
……(III)
from Equation (1):-
 F(x) = f(x) + A ∅(x)
 F(a) = f(a)+ A ∅(a) ……..(IV)
 F(b) = f(b)+ A ∅(b) ………(V)
 Now from Equation (II), we get:-
F(a) =F(b)

20. 𝑓 𝑎 + 𝐴 ∅ 𝑎 = 𝑓 𝑏 + 𝐴 ∅ 𝑏
𝐴 ∅ 𝑎 − 𝐴 ∅ 𝑏 = 𝑓 𝑏 − 𝑓(𝑎)
−𝐴 ∅ 𝑏 − ∅ 𝑎 = 𝑓 𝑏 − 𝑓(𝑎)
− 𝐴 =
𝑓 𝑏 − 𝑓(𝑎)
∅ 𝑏 − ∅(𝑎)
……….(VI)
Again from Equation (I) we get :
𝐹 𝑥 = 𝑓 𝑥 + 𝐴 ∅ 𝑥
𝐹′
𝑥 = 𝑓′
𝑥 + 𝐴 ∅ 𝑥
𝐹′
𝑐 = 𝑓′
𝑐 + 𝐴 ∅(𝑐)

21. Now From Equation (III)
Ans..
Hence Proved

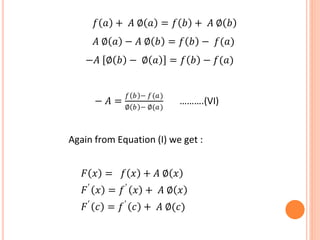
22. EXAMPLE:-
VERIFY CAUCHY’S MEAN VALUE THEOREM FOR FUNCTION
AND IN INTERVAL [1,2]
It is given that,
𝑓 𝑥 = 𝑥2
+ 1
∅ 𝑥 = 2𝑥3
𝑎, 𝑏 = 1,2
Since a=1 , b=2
By the Cauchy’s Mean Value Theorem,
𝑓′ (𝑐)
∅′ (𝑐)
=
𝑓 𝑏 −𝑓(𝑎)
∅ 𝑏 −∅(𝑎)
……(I)
𝑓 𝑥 = 𝑥2
+ 1
𝑓 𝑎 = 𝑎2
+ 1
𝑓 𝑎 = 1 + 1

23. And 𝑓 𝑏 = 22
+ 1
𝑓 𝑏 = 4 + 1 = 5
∅ 𝑥 = 2𝑥3
∅ 𝑎 = 2𝑎3
∅ 𝑎 = 2 × 13
∅ 𝑎 = 2
And ∅ 𝑏 = 2 + 23
= 16
Since 𝑓 𝑥 = 𝑥2
+ 1
There fore 𝑓′
𝑥 = 2𝑥
So 𝑓′
𝑐 = 2𝑐
And ∅ 𝑥 = 2𝑥3
∅′
𝑥 = 6𝑥2
∅′
𝑐 = 6𝑐2

24. Hence from Equation (I) :
Since [a<c<b]
Clearly lies in (1,2)
Hence Cauchy’s Mean Value Theorem is
verified.

25. THANK YOU