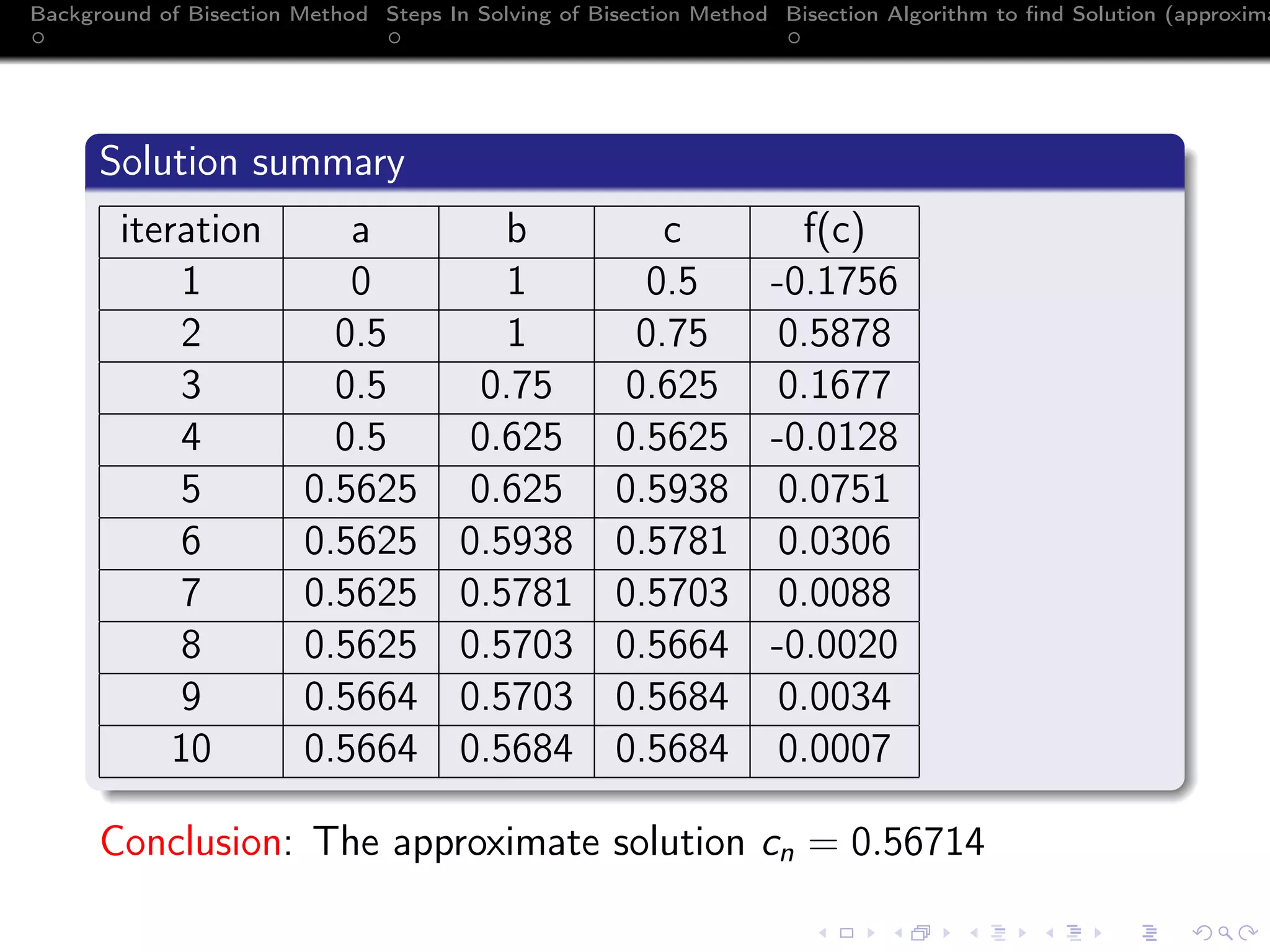
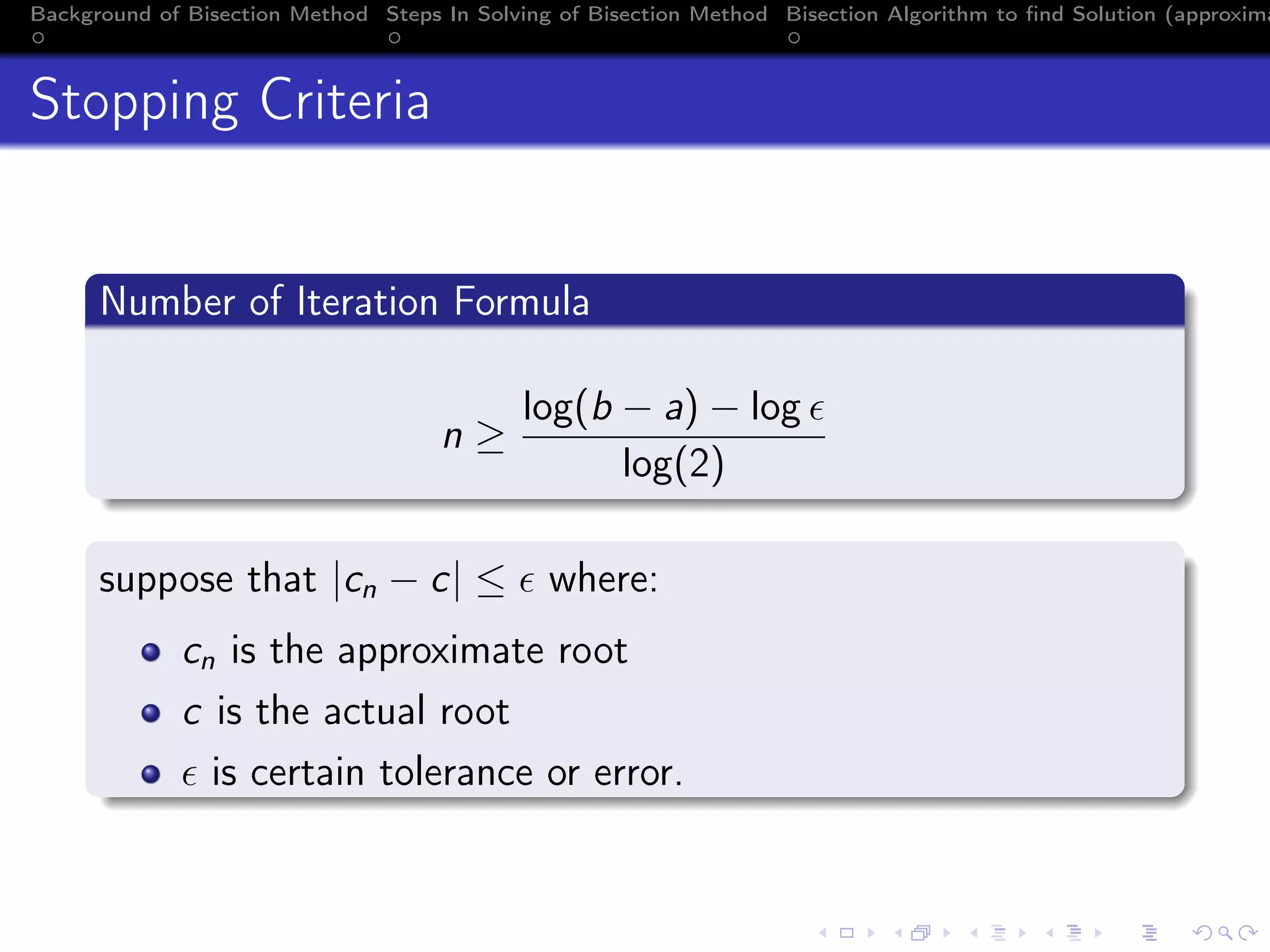
The document describes the bisection method, also known as interval halving, for finding roots of nonlinear equations. It discusses Bolzano's theorem which guarantees a root between intervals where the function changes sign. The bisection algorithm iteratively halves intervals and chooses the sub-interval based on the function value. The number of iterations needed for a given tolerance can be determined from the log formula provided. An example finds the root of an exponential equation in 10 iterations to within tolerance 10^-3.

1. Bisection (Dichotomy) Method
Numerical Analysis
Isaac Amornortey Yowetu
NIMS-Ghana
August 29, 2020

2. Background of Bisection Method Steps In Solving of Bisection Method Bisection Algorithm to find Solution (approxima
Outline
1 Background of Bisection Method
2 Steps In Solving of Bisection Method
Graphical Example
3 Bisection Algorithm to find Solution (approximate)
4 Derivation of the number of Iteration
5 Application of Bisection Method

3. Background of Bisection Method Steps In Solving of Bisection Method Bisection Algorithm to find Solution (approxima
Background of Bisection Method
Introduction
This method is also know as the Interval halving method.
It is method based on division of halves.
It is one of the bracketing method in finding roots on a
nonlinear equations.
It is noted to be based on Bolzano’s theorem for
continuous functions.
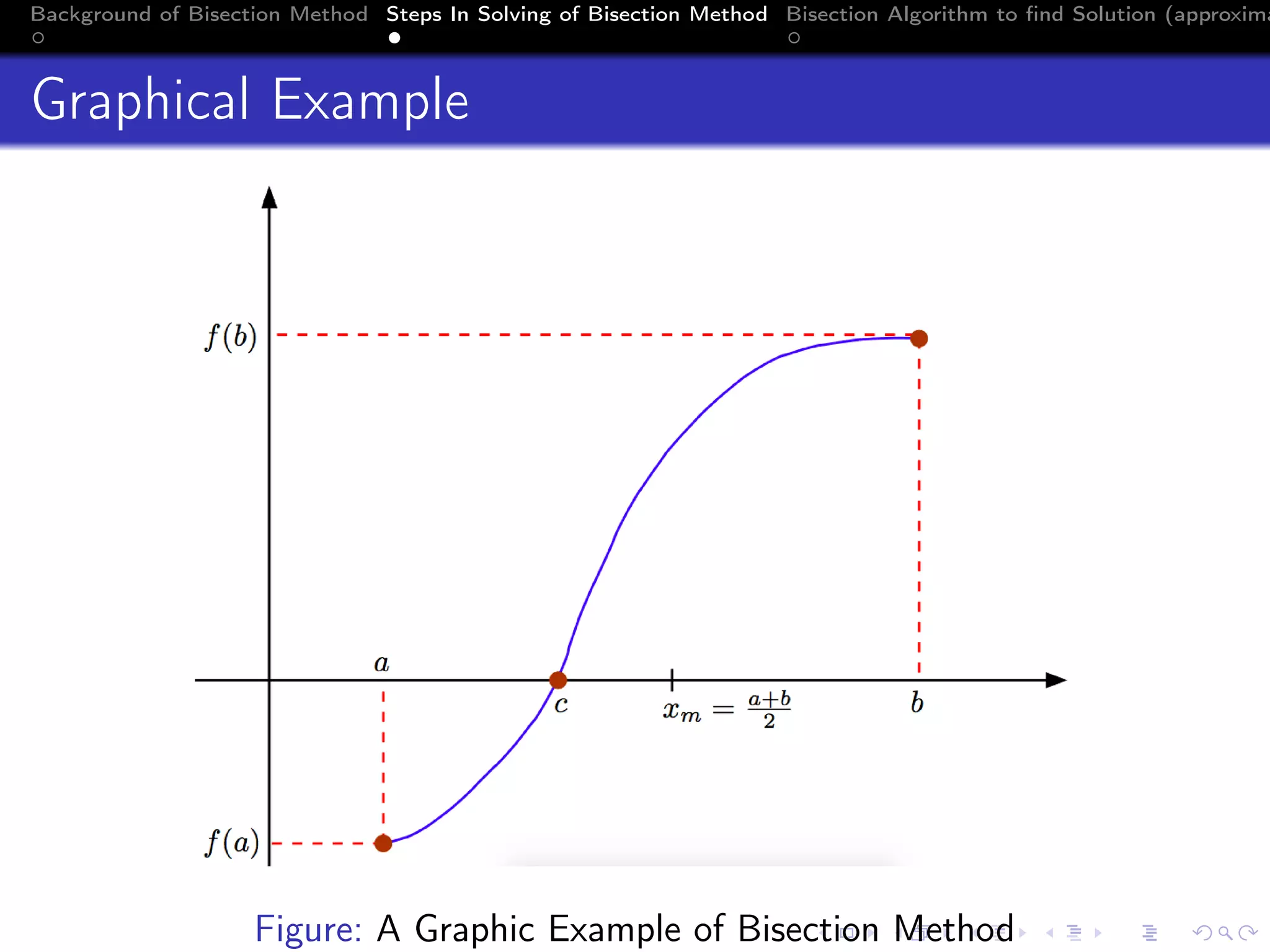
Theorem (Bolzano)
If a function f (x) is continuous on an interval [a, b] and
f (a) · f (b) < 0, then a value c ∈ (a, b) exists for which
f (c) = 0.

4. Background of Bisection Method Steps In Solving of Bisection Method Bisection Algorithm to find Solution (approxima
Graphical Example
Figure: A Graphic Example of Bisection Method

5. Background of Bisection Method Steps In Solving of Bisection Method Bisection Algorithm to find Solution (approxima
Bisection Algorithm
if f (a) · f (b) < 0:
root exists
else:
root doesn’t exist
Iteration Processes when root exists
1 Let c = a+b
2
2 If f (c) = 0, stop! c is the root.
3 if f (a) · f (c) < 0:
set b ← c
4 else if:
set a ← c
5 Go to the beginning and repeat till convergence.

6. Background of Bisection Method Steps In Solving of Bisection Method Bisection Algorithm to find Solution (approxima
Stopping Criteria
Number of Iteration Formula
n ≥
log(b − a) − log
log(2)
suppose that |cn − c| ≤ where:
cn is the approximate root
c is the actual root
is certain tolerance or error.

7. Background of Bisection Method Steps In Solving of Bisection Method Bisection Algorithm to find Solution (approxima
Graphical Example
Figure: A Graphic Example of Bisection number of iteration

8. Background of Bisection Method Steps In Solving of Bisection Method Bisection Algorithm to find Solution (approxima
Derivation of the number of iteration for
convergence.
|c − c1| ≤
b1 − a1
2
=
1
2
(b1 − a1) (1)
|c − c2| ≤
b2 − a2
2
=
1
2
(b2 − a2) (2)
=
1
2
b1 + a1
2
− a1 (3)
=
1
22
(b1 − a1) (4)
|c − c3| ≤
b3 − a3
2
=
1
2
(b3 − a3) (5)
=
1
2
b2 + a2
2
− a2 (6)

9. Background of Bisection Method Steps In Solving of Bisection Method Bisection Algorithm to find Solution (approxima
Derivation Continues...
=
1
22
(b2 − a2) (7)
=
1
22
(
b1 + a1
2
− a1) (8)
=
1
23
(b1 − a1) (9)
... (10)
|c − cn| ≤
1
2n
(b1 − a1) (11)

10. Background of Bisection Method Steps In Solving of Bisection Method Bisection Algorithm to find Solution (approxima
Finding n the number of iteration
≥
b1 − a1
2n
≥ |cn − c|
2n
· ≥ (b1 − a1)
log(2n
· ) ≥ log(b1 − a1)
log(2n
) + log( ) ≥ log(b1 − a1)
n · log(2) ≥ log(b1 − a1) − log( )
n ≥
log(b1 − a1) − log( )
log(2)

11. Background of Bisection Method Steps In Solving of Bisection Method Bisection Algorithm to find Solution (approxima
Application of Bisection Method
Example 1
Find a root of xex
= 1 on I = [0, 1] using Bisection method.
Considering our f (x) = xex
− 1 = 0
Solution
f (0) = 0 · e0
− 1 = −1
f (1) = 1 · e1
− 1 = 1.7183
f (0) · f (1) < 0, hence c ∈ [0, 1].
c1 =
1 + 0
2
= 0.5 (12)
f (c1) = −0.1756 (13)
choose [a2, b2] = [0.5, 1]

12. Background of Bisection Method Steps In Solving of Bisection Method Bisection Algorithm to find Solution (approxima
Solution Continue...
c2 =
0.5 + 1
2
= 0.75 (14)
f (c2) = 0.5878 (15)
choose [a3, b3] = [0.5, 0.75]
c3 =
0.5 + 0.75
2
= 0.625 (16)
f (c3) = 0.1677 (17)
choose [a4, b4] = [0.5, 0.625]

13. Background of Bisection Method Steps In Solving of Bisection Method Bisection Algorithm to find Solution (approxima
Solution summary
iteration a b c f(c)
1 0 1 0.5 -0.1756
2 0.5 1 0.75 0.5878
3 0.5 0.75 0.625 0.1677
4 0.5 0.625 0.5625 -0.0128
5 0.5625 0.625 0.5938 0.0751
6 0.5625 0.5938 0.5781 0.0306
7 0.5625 0.5781 0.5703 0.0088
8 0.5625 0.5703 0.5664 -0.0020
9 0.5664 0.5703 0.5684 0.0034
10 0.5664 0.5684 0.5684 0.0007
Conclusion: The approximate solution cn = 0.56714

14. Background of Bisection Method Steps In Solving of Bisection Method Bisection Algorithm to find Solution (approxima
Question: Determining the number of iterations
Problem
One root of the equation ex
− 3x2
= 0 lies in the interval
(3,4). Find the least number of iterations of the bisection
method so that | | < 10−3
.
Solution
n ≥
log(4 − 3) − log(10−3
)
log(2)
= 9.9658
∴ n 10

15. Background of Bisection Method Steps In Solving of Bisection Method Bisection Algorithm to find Solution (approxima
Question: Determining the number of iterations
Problem
One root of the equation xex
− 1 = 0 lies in the interval (0,1).
Find the least number of iterations of the bisection method so
that | | < 10−5
.
Solution
n ≥
log(1 − 0) − log(10−5
)
log(2)
= 16.6096
∴ n 17

16. Background of Bisection Method Steps In Solving of Bisection Method Bisection Algorithm to find Solution (approxima
End
THANK YOU